आपने पिछले अभ्यास में देखा कि हमारे नेटवर्क में केवल हिडन लेयर्स जोड़ने से नॉन-लीनियरिटी को दर्शाना पर्याप्त नहीं था। लीनियर ऑपरेशन्स पर किए गए लीनियर ऑपरेशन्स अभी भी लीनियर ही रहते हैं।
आप न्यूरल नेटवर्क को मूल्यों के बीच अरेखीय संबंधों को सीखने के लिए कैसे कॉन्फ़िगर कर सकते हैं? हमें मॉडल में अरेखीय गणितीय संक्रियाओं को शामिल करने का कोई तरीका चाहिए।
यदि यह आपको कुछ जाना-पहचाना सा लग रहा है, तो इसका कारण यह है कि हमने पाठ्यक्रम में पहले ही एक रैखिक मॉडल के आउटपुट पर गैर-रैखिक गणितीय संक्रियाओं को लागू किया है। लॉजिस्टिक रिग्रेशन मॉड्यूल में, हमने एक रैखिक रिग्रेशन मॉडल को सिग्मॉइड फ़ंक्शन के माध्यम से मॉडल के आउटपुट को गुजारकर 0 से 1 तक एक सतत मान (जो प्रायिकता को दर्शाता है) आउटपुट करने के लिए अनुकूलित किया था।
हम इसी सिद्धांत को अपने न्यूरल नेटवर्क पर भी लागू कर सकते हैं। आइए, अभ्यास 2 में दिखाए गए अपने मॉडल को फिर से देखें, लेकिन इस बार, प्रत्येक नोड का मान आउटपुट करने से पहले, हम पहले सिग्मॉइड फ़ंक्शन लागू करेंगे:
प्ले बटन के दाईं ओर स्थित >| बटन पर क्लिक करके प्रत्येक नोड की गणनाओं को चरणबद्ध तरीके से देखें। ग्राफ के नीचे स्थित गणना पैनल में प्रत्येक नोड के मान की गणना के लिए किए गए गणितीय संक्रियाओं की समीक्षा करें। ध्यान दें कि प्रत्येक नोड का आउटपुट अब पिछली परत के नोड्स के रैखिक संयोजन का सिग्मॉइड रूपांतरण है, और आउटपुट मान 0 और 1 के बीच सीमित हैं।
यहां, सिग्मॉइड तंत्रिका नेटवर्क के लिए एक सक्रियण फ़ंक्शन के रूप में कार्य करता है, जो एक न्यूरॉन के आउटपुट मान का एक गैर-रेखीय रूपांतरण है, इससे पहले कि मान को तंत्रिका नेटवर्क की अगली परत की गणनाओं के लिए इनपुट के रूप में पारित किया जाए।
अब जब हमने एक्टिवेशन फ़ंक्शन जोड़ दिया है, तो लेयर्स जोड़ने का प्रभाव और भी बढ़ जाता है। नॉनलाइनैरिटीज़ को एक के ऊपर एक स्टैक करने से हम इनपुट और प्रेडिक्टेड आउटपुट के बीच बहुत जटिल संबंधों को मॉडल कर सकते हैं। संक्षेप में, प्रत्येक लेयर प्रभावी रूप से रॉ इनपुट पर एक अधिक जटिल, उच्च-स्तरीय फ़ंक्शन सीख रही है। यदि आप यह समझना चाहते हैं कि यह कैसे काम करता है, तो क्रिस ओलाह का उत्कृष्ट ब्लॉग पोस्ट देखें।
सामान्य सक्रियण कार्य
तीन गणितीय फलन जिनका उपयोग आमतौर पर सक्रियण फलन के रूप में किया जाता है, वे हैं सिग्मॉइड, टैन्ह और रीएलयू।
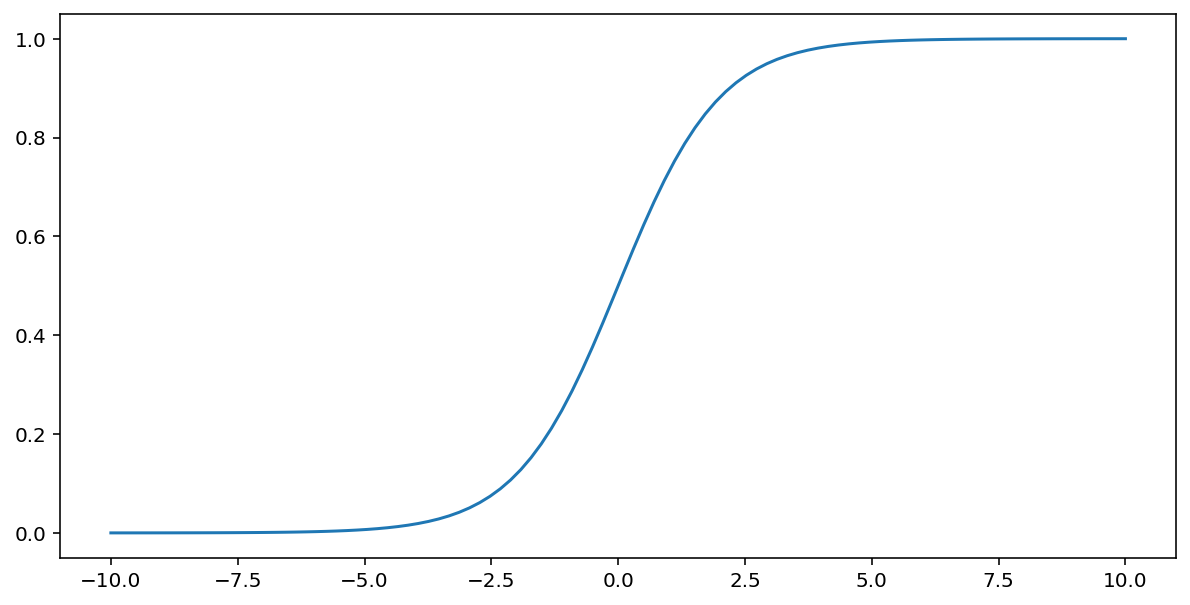
सिग्मॉइड फ़ंक्शन (जिसकी चर्चा ऊपर की गई है) इनपुट $x$ पर निम्नलिखित रूपांतरण करता है, जिससे 0 और 1 के बीच एक आउटपुट मान प्राप्त होता है:
\[F(x)=\frac{1} {1+e^{-x}}\]
यह इस फ़ंक्शन का ग्राफ है:
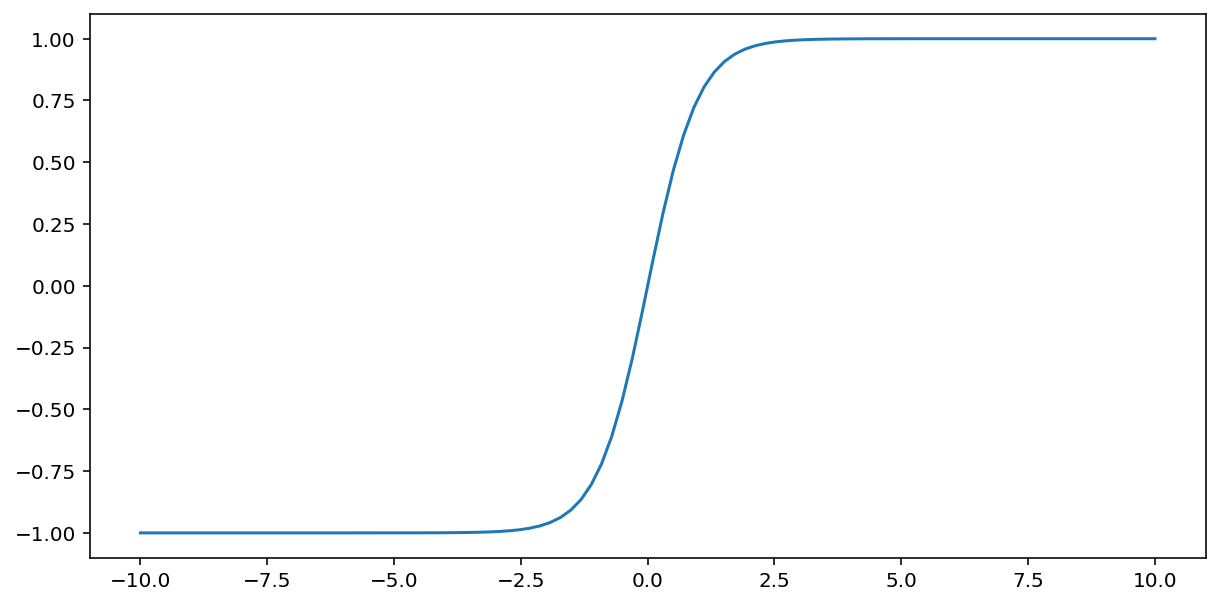
tanh (हाइपरबोलिक टेंजेंट का संक्षिप्त रूप) फ़ंक्शन इनपुट $x$ को रूपांतरित करके -1 और 1 के बीच एक आउटपुट मान उत्पन्न करता है:
\[F(x)=tanh(x)\]
यह इस फ़ंक्शन का ग्राफ है:
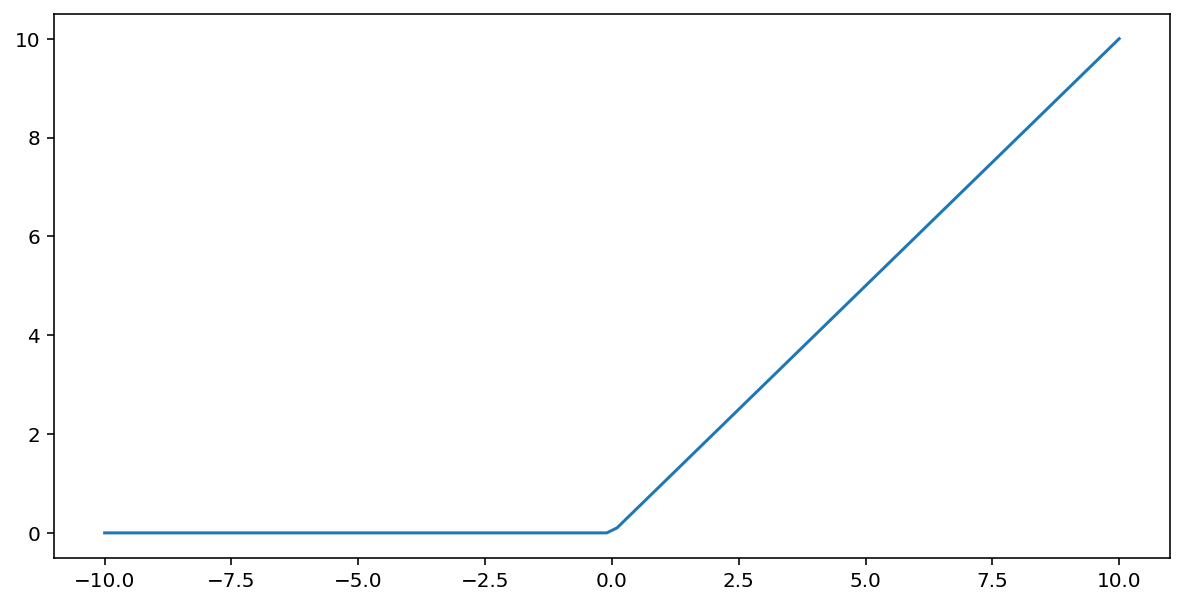
रेक्टिफाइड लीनियर यूनिट एक्टिवेशन फंक्शन (संक्षेप में ReLU ) निम्नलिखित एल्गोरिदम का उपयोग करके आउटपुट को रूपांतरित करता है:
- यदि इनपुट मान $x$ 0 से कम है, तो 0 लौटाएँ।
- यदि इनपुट मान $x$ 0 से बड़ा या बराबर है, तो इनपुट मान लौटाएँ।
ReLU को max() फ़ंक्शन का उपयोग करके गणितीय रूप से दर्शाया जा सकता है:
यह इस फ़ंक्शन का ग्राफ है:
ReLU, सिग्मॉइड या टैन्ह जैसे स्मूथ फंक्शन की तुलना में एक्टिवेशन फंक्शन के रूप में थोड़ा बेहतर काम करता है, क्योंकि न्यूरल नेटवर्क ट्रेनिंग के दौरान इसमें वैनिशिंग ग्रेडिएंट की समस्या कम होती है। साथ ही, ReLU की गणना करना भी इन फंक्शन की तुलना में काफी आसान है।
अन्य सक्रियण कार्य
व्यवहार में, कोई भी गणितीय फलन सक्रियण फलन के रूप में कार्य कर सकता है। मान लीजिए कि \(\sigma\) यह हमारे सक्रियण फ़ंक्शन को दर्शाता है। नेटवर्क में एक नोड का मान निम्नलिखित सूत्र द्वारा दिया जाता है:
Keras कई एक्टिवेशन फ़ंक्शंस के लिए अंतर्निहित समर्थन प्रदान करता है। फिर भी, हम ReLU से शुरुआत करने की सलाह देते हैं।
सारांश
निम्नलिखित वीडियो में आपने अब तक न्यूरल नेटवर्क के निर्माण के बारे में जो कुछ भी सीखा है, उसका संक्षिप्त विवरण दिया गया है:
अब हमारे मॉडल में वे सभी मानक घटक शामिल हैं जिनका अर्थ लोग आमतौर पर न्यूरल नेटवर्क से निकालते हैं:
- न्यूरॉन्स के समान, परतों में व्यवस्थित नोड्स का एक समूह।
- सीखे गए भारों और पूर्वाग्रहों का एक समूह जो प्रत्येक न्यूरल नेटवर्क परत और उसके नीचे वाली परत के बीच संबंधों को दर्शाता है। नीचे वाली परत एक अन्य न्यूरल नेटवर्क परत हो सकती है, या किसी अन्य प्रकार की परत हो सकती है।
- एक सक्रियण फ़ंक्शन जो एक परत में प्रत्येक नोड के आउटपुट को रूपांतरित करता है। विभिन्न परतों में अलग-अलग सक्रियण फ़ंक्शन हो सकते हैं।
एक बात ध्यान देने योग्य है: न्यूरल नेटवर्क हमेशा फीचर क्रॉस से बेहतर नहीं होते हैं, लेकिन न्यूरल नेटवर्क एक लचीला विकल्प प्रदान करते हैं जो कई मामलों में अच्छी तरह से काम करता है।
