در تمرین قبلی دیدید که فقط اضافه کردن لایههای پنهان به شبکه برای نمایش غیرخطی بودن کافی نبود. عملیات خطی انجام شده روی عملیات خطی، همچنان خطی هستند.
چگونه میتوان یک شبکه عصبی را طوری پیکربندی کرد که روابط غیرخطی بین مقادیر را یاد بگیرد؟ ما به روشی نیاز داریم تا عملیات ریاضی غیرخطی را در یک مدل وارد کنیم.
اگر این موضوع تا حدودی آشنا به نظر میرسد، به این دلیل است که ما در واقع عملیات ریاضی غیرخطی را در اوایل دوره بر روی خروجی یک مدل خطی اعمال کردهایم. در ماژول رگرسیون لجستیک ، ما یک مدل رگرسیون خطی را برای خروجی یک مقدار پیوسته از 0 تا 1 (که نشان دهنده یک احتمال است) با عبور خروجی مدل از یک تابع سیگموئید تطبیق دادیم.
میتوانیم همین اصل را در شبکه عصبی خود اعمال کنیم. بیایید مدل خود را از تمرین ۲ که قبلاً انجام دادیم، دوباره بررسی کنیم، اما این بار، قبل از نمایش مقدار هر گره، ابتدا تابع سیگموئید را اعمال خواهیم کرد:
با کلیک بر روی دکمهی >| (در سمت راست دکمهی پخش)، محاسبات هر گره را گام به گام انجام دهید. عملیات ریاضی انجام شده برای محاسبهی مقدار هر گره را در پنل محاسبات زیر نمودار مرور کنید. توجه داشته باشید که خروجی هر گره اکنون یک تبدیل سیگموئیدی از ترکیب خطی گرهها در لایهی قبلی است و مقادیر خروجی همگی بین ۰ و ۱ قرار گرفتهاند.
در اینجا، سیگموئید به عنوان یک تابع فعالسازی برای شبکه عصبی عمل میکند، یک تبدیل غیرخطی از مقدار خروجی نورون قبل از اینکه مقدار به عنوان ورودی به محاسبات لایه بعدی شبکه عصبی منتقل شود.
حالا که یک تابع فعالسازی اضافه کردهایم، اضافه کردن لایهها تأثیر بیشتری دارد. روی هم قرار دادن غیرخطیها روی غیرخطیها به ما امکان میدهد روابط بسیار پیچیده بین ورودیها و خروجیهای پیشبینیشده را مدلسازی کنیم. به طور خلاصه، هر لایه به طور مؤثر یک تابع پیچیدهتر و سطح بالاتر را روی ورودیهای خام یاد میگیرد. اگر میخواهید درک بیشتری از نحوه کار این روش داشته باشید، به پست وبلاگ عالی کریس اولا مراجعه کنید.
توابع فعالسازی رایج
سه تابع ریاضی که معمولاً به عنوان توابع فعالسازی استفاده میشوند عبارتند از سیگموئید، تانژانت و ReLU.
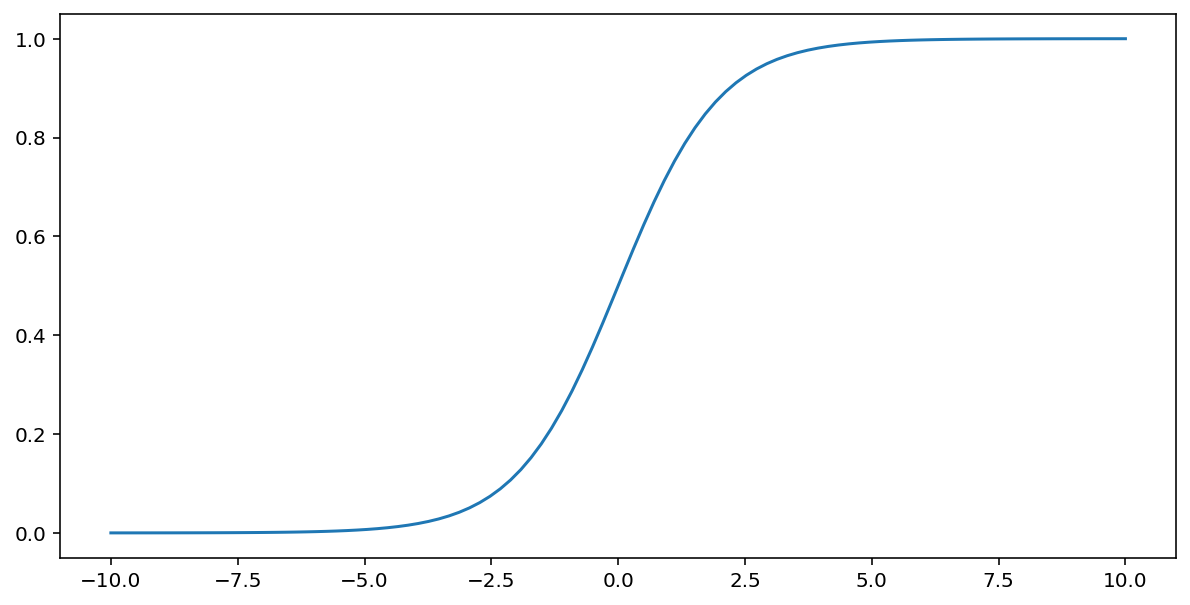
تابع سیگموئید (که در بالا مورد بحث قرار گرفت) تبدیل زیر را روی ورودی $x$ انجام میدهد و مقداری خروجی بین ۰ و ۱ تولید میکند:
\[F(x)=\frac{1} {1+e^{-x}}\]
نمودار این تابع به صورت زیر است:
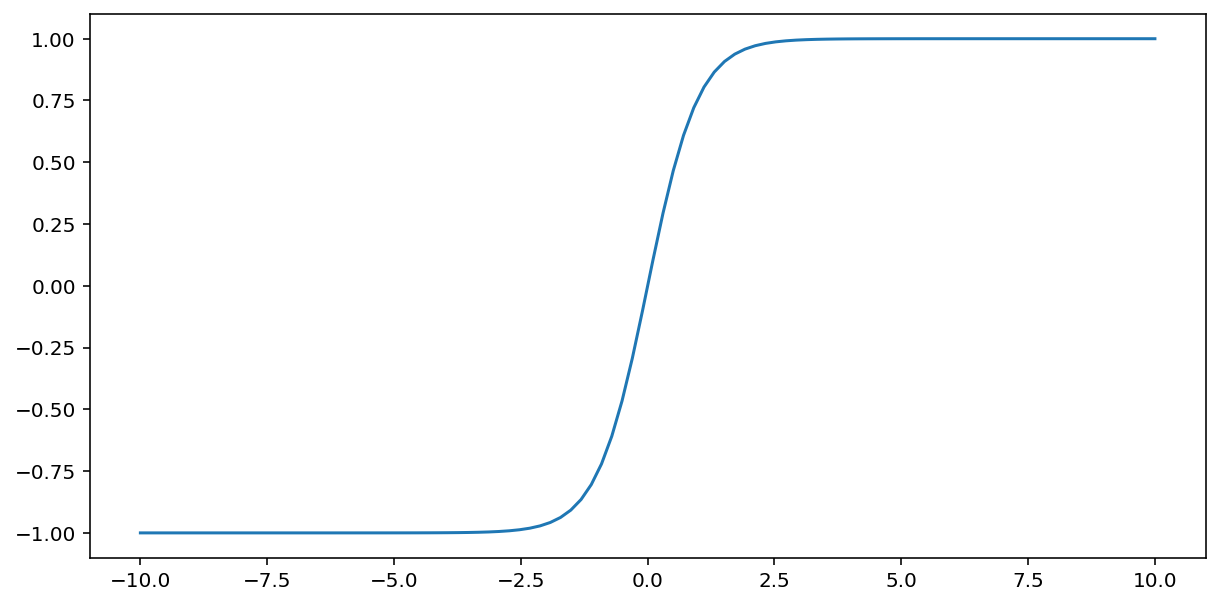
تابع tanh (مخفف "تانژانت هیپربولیک") ورودی $x$ را طوری تغییر میدهد که مقداری بین -1 و 1 در خروجی تولید کند:
\[F(x)=tanh(x)\]
نمودار این تابع به صورت زیر است:
تابع فعالسازی واحد خطی یکسو شده (یا به اختصار ReLU ) خروجی را با استفاده از الگوریتم زیر تبدیل میکند:
- اگر مقدار ورودی $x$ کمتر از 0 باشد، 0 را برمیگرداند.
- اگر مقدار ورودی $x$ بزرگتر یا مساوی 0 باشد، مقدار ورودی را برمیگرداند.
ReLU را میتوان با استفاده از تابع max() به صورت ریاضی نمایش داد:
نمودار این تابع به صورت زیر است:
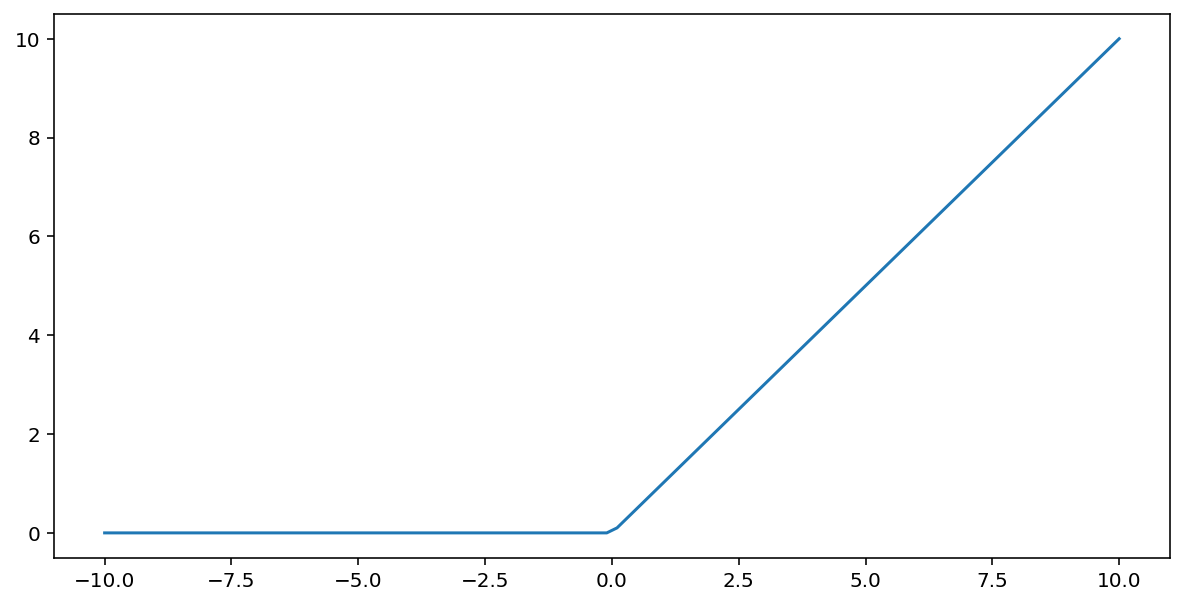
ReLU اغلب به عنوان یک تابع فعالسازی کمی بهتر از یک تابع هموار مانند سیگموئید یا tanh عمل میکند، زیرا در طول آموزش شبکه عصبی کمتر مستعد مشکل محو شدن گرادیان است. محاسبه ReLU نیز به طور قابل توجهی آسانتر از این توابع است.
سایر توابع فعالسازی
در عمل، هر تابع ریاضی میتواند به عنوان یک تابع فعالسازی عمل کند. فرض کنید که \(\sigma\) نشان دهنده تابع فعال سازی ما است. مقدار یک گره در شبکه با فرمول زیر داده می شود:
Keras پشتیبانی آمادهای برای بسیاری از توابع فعالسازی ارائه میدهد. با این حال، ما همچنان توصیه میکنیم با ReLU شروع کنید.
خلاصه
ویدیوی زیر خلاصهای از هر آنچه تاکنون در مورد نحوه ساخت شبکههای عصبی آموختهاید را ارائه میدهد:
اکنون مدل ما تمام اجزای استانداردی را که معمولاً مردم هنگام اشاره به یک شبکه عصبی در نظر دارند، دارد:
- مجموعهای از گرهها، مشابه نورونها، که در لایههایی سازماندهی شدهاند.
- مجموعهای از وزنها و بایاسهای آموختهشده که نشاندهندهی ارتباط بین هر لایه شبکه عصبی و لایهی زیرین آن است. لایهی زیرین ممکن است یک لایهی شبکهی عصبی دیگر یا نوع دیگری از لایه باشد.
- یک تابع فعالسازی که خروجی هر گره در یک لایه را تبدیل میکند. لایههای مختلف ممکن است توابع فعالسازی متفاوتی داشته باشند.
یک نکته: شبکههای عصبی لزوماً همیشه بهتر از ترکیب ویژگیها نیستند، اما شبکههای عصبی جایگزین انعطافپذیری ارائه میدهند که در بسیاری از موارد به خوبی کار میکند.
