Sie haben in der vorherigen Übung gesehen, dass das bloße Hinzufügen verborgener Schichten zu unserem Netzwerk nicht ausreicht, um Nichtlinearitäten abzubilden. Lineare Operationen, die auf lineare Operationen angewendet werden, sind immer noch linear.
Wie kann man ein neuronales Netzwerk so konfigurieren, dass es nichtlineare Beziehungen zwischen Werten lernt? Wir benötigen eine Möglichkeit, nichtlineare mathematische Operationen in ein Modell einzufügen.
Falls Ihnen das bekannt vorkommt, liegt das daran, dass wir im Laufe des Kurses bereits nichtlineare mathematische Operationen auf die Ausgabe eines linearen Modells angewendet haben. Im Modul „Logistische Regression“ haben wir ein lineares Regressionsmodell so angepasst, dass es einen kontinuierlichen Wert zwischen 0 und 1 (der eine Wahrscheinlichkeit darstellt) ausgibt, indem wir die Modellausgabe durch eine Sigmoidfunktion geleitet haben.
Wir können dasselbe Prinzip auf unser neuronales Netzwerk anwenden. Schauen wir uns unser Modell aus Übung 2 noch einmal an, aber diesmal wenden wir vor der Ausgabe des Wertes jedes Knotens zuerst die Sigmoid-Funktion an:
Versuchen Sie, die Berechnungen jedes Knotens schrittweise durchzugehen, indem Sie auf die Schaltfläche >| (rechts neben der Wiedergabetaste) klicken. Überprüfen Sie die mathematischen Operationen, die zur Berechnung jedes Knotenwertes durchgeführt wurden, im Berechnungsfeld unterhalb des Diagramms. Beachten Sie, dass die Ausgabe jedes Knotens nun eine Sigmoid-Transformation der Linearkombination der Knoten der vorherigen Ebene ist und die Ausgabewerte alle zwischen 0 und 1 liegen.
Hierbei dient die Sigmoidfunktion als Aktivierungsfunktion für das neuronale Netzwerk, eine nichtlineare Transformation des Ausgabewerts eines Neurons, bevor der Wert als Eingabe für die Berechnungen der nächsten Schicht des neuronalen Netzwerks verwendet wird.
Nachdem wir eine Aktivierungsfunktion hinzugefügt haben, gewinnt das Hinzufügen weiterer Schichten an Bedeutung. Durch das Stapeln von Nichtlinearitäten können wir sehr komplexe Zusammenhänge zwischen den Eingaben und den vorhergesagten Ausgaben modellieren. Kurz gesagt: Jede Schicht lernt im Prinzip eine komplexere Funktion höherer Ordnung anhand der Rohdaten. Wenn Sie ein besseres Verständnis dafür entwickeln möchten, wie das funktioniert, lesen Sie den hervorragenden Blogbeitrag von Chris Olah .
Gemeinsame Aktivierungsfunktionen
Drei mathematische Funktionen, die häufig als Aktivierungsfunktionen verwendet werden, sind Sigmoid, Tanh und ReLU.
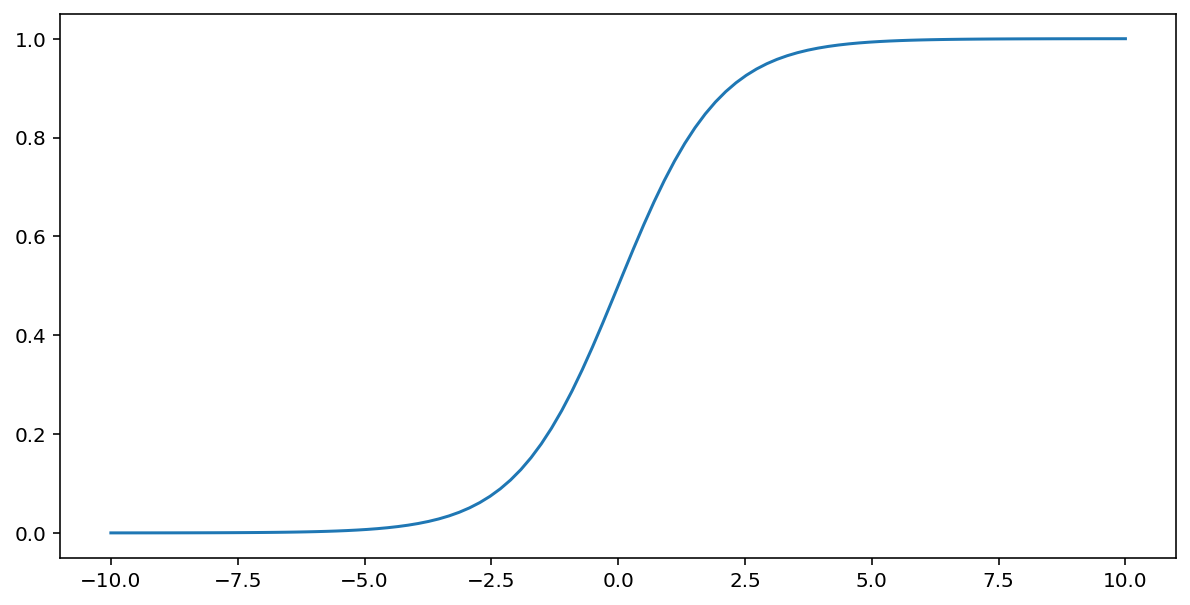
Die oben beschriebene Sigmoidfunktion transformiert den Eingabewert $x$ wie folgt und erzeugt einen Ausgabewert zwischen 0 und 1:
\[F(x)=\frac{1} {1+e^{-x}}\]
Hier ist eine grafische Darstellung dieser Funktion:
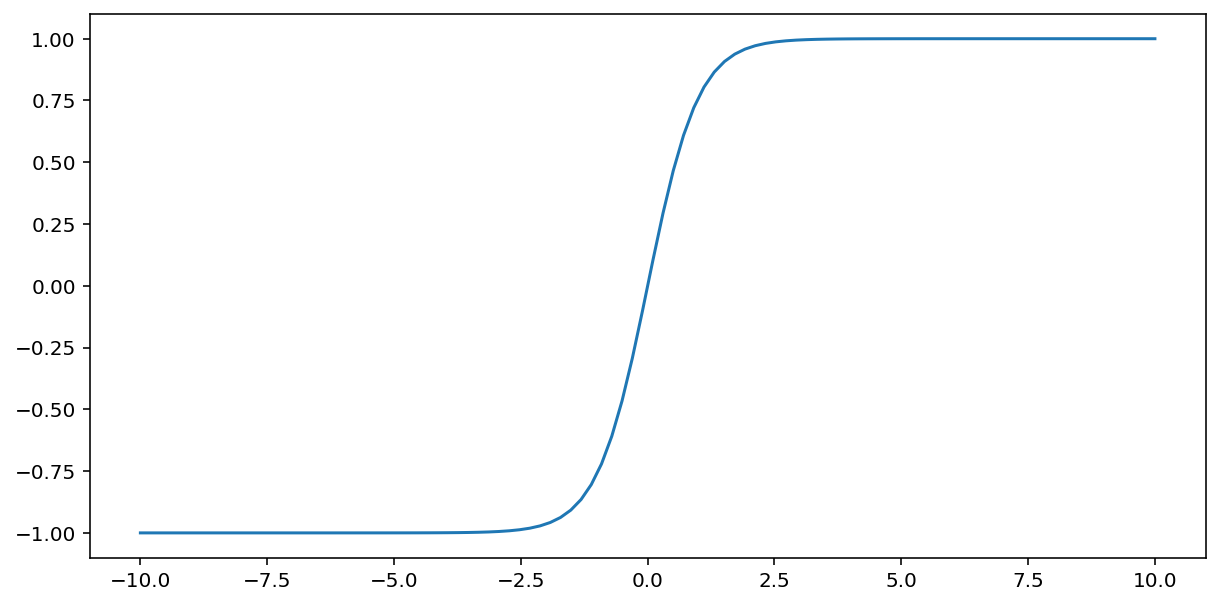
Die tanh-Funktion (kurz für „hyperbolischer Tangens“) transformiert den Eingabewert $x$ und erzeugt einen Ausgabewert zwischen –1 und 1:
\[F(x)=tanh(x)\]
Hier ist eine grafische Darstellung dieser Funktion:
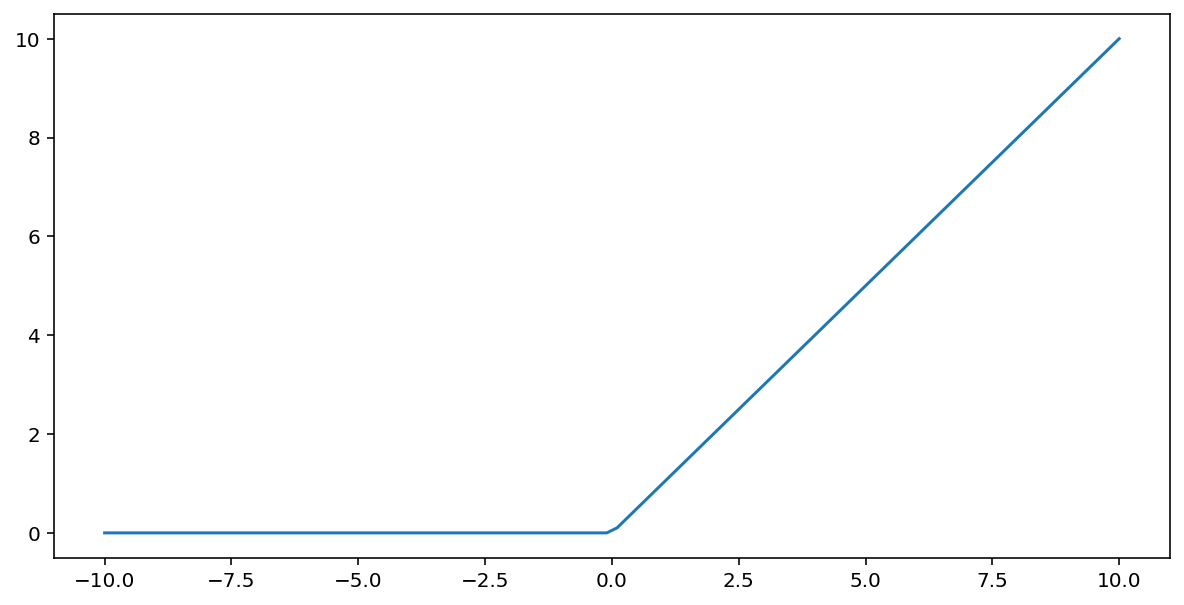
Die ReLU -Aktivierungsfunktion ( Rectified Linear Unit ) transformiert die Ausgabe mithilfe des folgenden Algorithmus:
- Wenn der Eingabewert $x$ kleiner als 0 ist, gib 0 zurück.
- Wenn der Eingabewert $x$ größer oder gleich 0 ist, gib den Eingabewert zurück.
ReLU kann mathematisch mithilfe der Funktion max() dargestellt werden:
Hier ist eine grafische Darstellung dieser Funktion:
ReLU eignet sich als Aktivierungsfunktion oft etwas besser als glatte Funktionen wie Sigmoid oder Tanh, da es weniger anfällig für das Problem des verschwindenden Gradienten beim Training neuronaler Netze ist. Außerdem ist ReLU deutlich einfacher zu berechnen als diese Funktionen.
Andere Aktivierungsfunktionen
In der Praxis kann jede mathematische Funktion als Aktivierungsfunktion dienen. Angenommen, \(\sigma\) stellt unsere Aktivierungsfunktion dar. Der Wert eines Knotens im Netzwerk wird durch die folgende Formel gegeben:
Keras bietet standardmäßig Unterstützung für viele Aktivierungsfunktionen . Dennoch empfehlen wir, mit ReLU zu beginnen.
Zusammenfassung
Das folgende Video bietet eine Zusammenfassung von allem, was Sie bisher über den Aufbau neuronaler Netze gelernt haben:
Unser Modell verfügt nun über alle Standardkomponenten dessen, was man im Allgemeinen unter einem neuronalen Netzwerk versteht:
- Eine Reihe von Knoten, analog zu Neuronen, die in Schichten organisiert sind.
- Ein Satz gelernter Gewichte und Bias-Werte, die die Verbindungen zwischen jeder Schicht des neuronalen Netzes und der darunterliegenden Schicht darstellen. Die darunterliegende Schicht kann eine weitere Schicht des neuronalen Netzes oder eine andere Art von Schicht sein.
- Eine Aktivierungsfunktion, die die Ausgabe jedes Knotens in einer Schicht transformiert. Verschiedene Schichten können unterschiedliche Aktivierungsfunktionen haben.
Ein wichtiger Hinweis: Neuronale Netze sind nicht immer besser als Merkmalskreuzungen, bieten aber eine flexible Alternative, die in vielen Fällen gut funktioniert.
