Jaringan neural: Fungsi aktivasi

Anda telah melihat pada latihan sebelumnya bahwa hanya menambahkan lapisan tersembunyi ke jaringan kita saja tidak cukup untuk merepresentasikan nonlinieritas. Operasi linier yang dilakukan pada operasi linier tetaplah linier.

Bagaimana cara mengkonfigurasi jaringan saraf untuk mempelajari hubungan nonlinier antar nilai? Kita membutuhkan cara untuk memasukkan operasi matematika nonlinier ke dalam model.

Jika ini tampak agak familiar, itu karena kita sebenarnya telah menerapkan operasi matematika nonlinier pada output model linier sebelumnya dalam kursus ini. Dalam modul Regresi Logistik , kita mengadaptasi model regresi linier untuk menghasilkan nilai kontinu dari 0 hingga 1 (mewakili probabilitas) dengan melewatkan output model melalui fungsi sigmoid .

Kita dapat menerapkan prinsip yang sama pada jaringan saraf kita. Mari kita tinjau kembali model kita dari Latihan 2 sebelumnya, tetapi kali ini, sebelum menampilkan nilai setiap node, kita akan menerapkan fungsi sigmoid terlebih dahulu:

Cobalah menelusuri perhitungan setiap node dengan mengklik tombol >| (di sebelah kanan tombol putar). Tinjau operasi matematika yang dilakukan untuk menghitung setiap nilai node di panel Perhitungan di bawah grafik. Perhatikan bahwa output setiap node sekarang merupakan transformasi sigmoid dari kombinasi linier node di lapisan sebelumnya, dan nilai output semuanya berada di antara 0 dan 1.

Di sini, sigmoid berfungsi sebagai fungsi aktivasi untuk jaringan saraf, yaitu transformasi nonlinier dari nilai keluaran neuron sebelum nilai tersebut diteruskan sebagai masukan ke perhitungan lapisan berikutnya dari jaringan saraf.

Sekarang setelah kita menambahkan fungsi aktivasi, menambahkan lapisan akan memberikan dampak yang lebih besar. Menumpuk fungsi nonlinier di atas fungsi nonlinier memungkinkan kita untuk memodelkan hubungan yang sangat kompleks antara input dan output yang diprediksi. Singkatnya, setiap lapisan secara efektif mempelajari fungsi yang lebih kompleks dan tingkat yang lebih tinggi daripada input mentah. Jika Anda ingin mengembangkan intuisi lebih lanjut tentang cara kerjanya, lihat postingan blog Chris Olah yang sangat bagus .

Fungsi aktivasi umum

Tiga fungsi matematika yang umum digunakan sebagai fungsi aktivasi adalah sigmoid, tanh, dan ReLU.

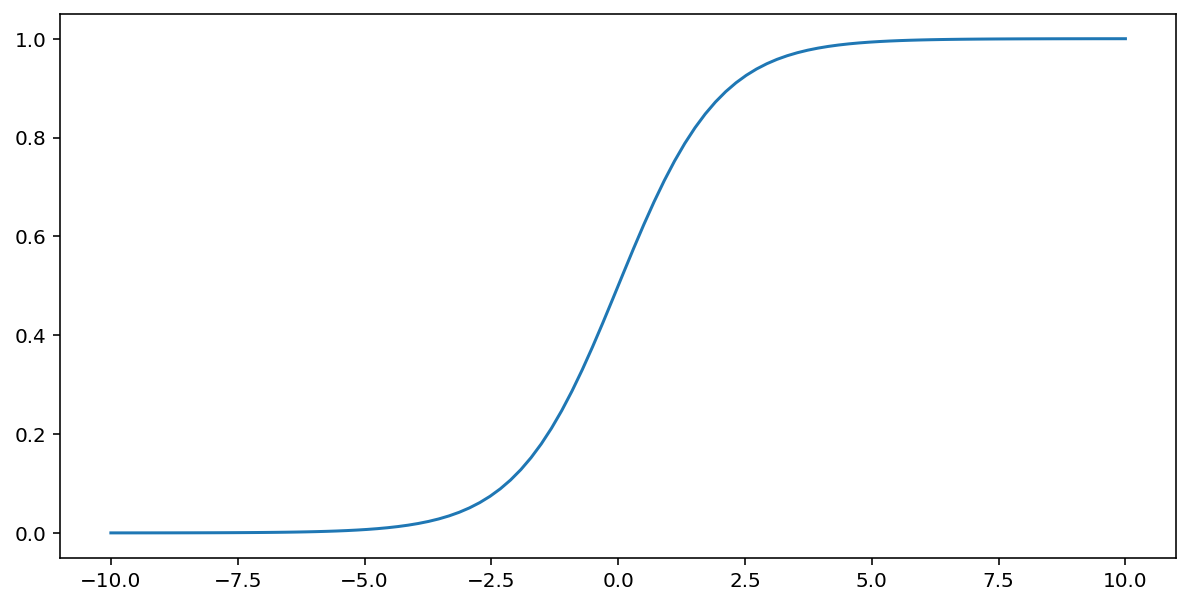
Fungsi sigmoid (yang dibahas di atas) melakukan transformasi berikut pada input $x$, menghasilkan nilai output antara 0 dan 1:

\[F(x)=\frac{1} {1+e^{-x}}\]

Berikut adalah grafik fungsi ini:

Gambar 4. Grafik fungsi sigmoid: kurva berbentuk S yang secara asimtotik mendekati sumbu x ketika x mendekati negatif tak hingga dan 1 ketika x mendekati tak hingga.
Gambar 4. Grafik fungsi sigmoid.

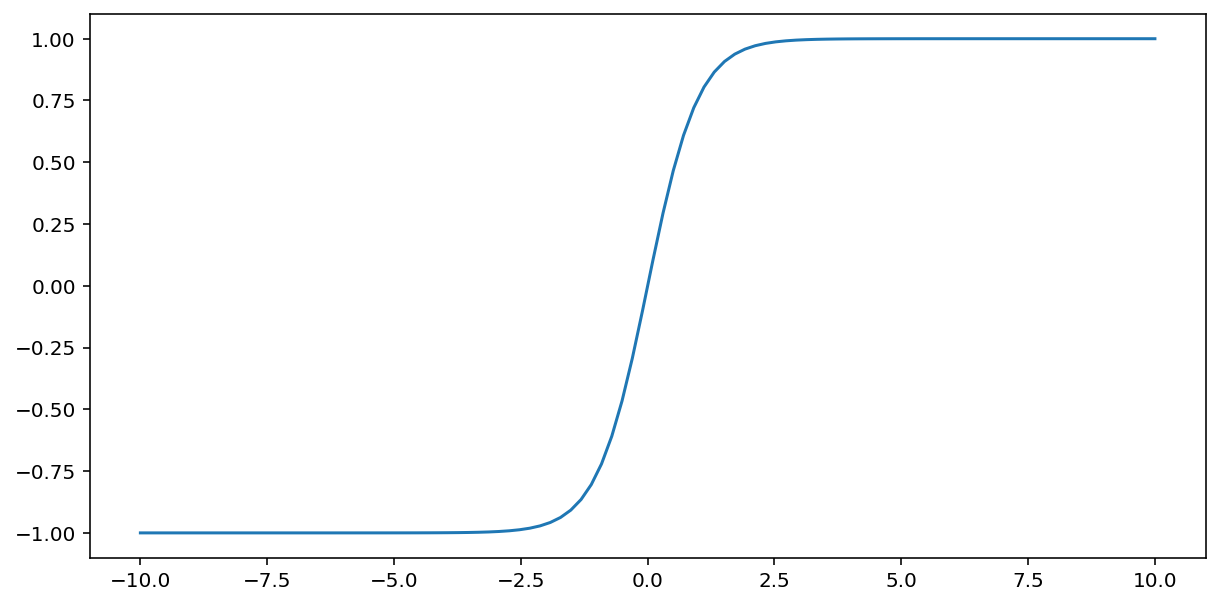
Fungsi tanh (singkatan dari "tangen hiperbolik") mengubah input $x$ untuk menghasilkan nilai output antara –1 dan 1:

\[F(x)=tanh(x)\]

Berikut adalah grafik fungsi ini:

Gambar 5. Grafik fungsi tanh: kurva berbentuk S yang sedikit lebih curam daripada fungsi sigmoid, yang secara asimtotik mendekati –1 ketika x mendekati negatif tak hingga dan 1 ketika x mendekati tak hingga.
Gambar 5. Grafik fungsi tanh.

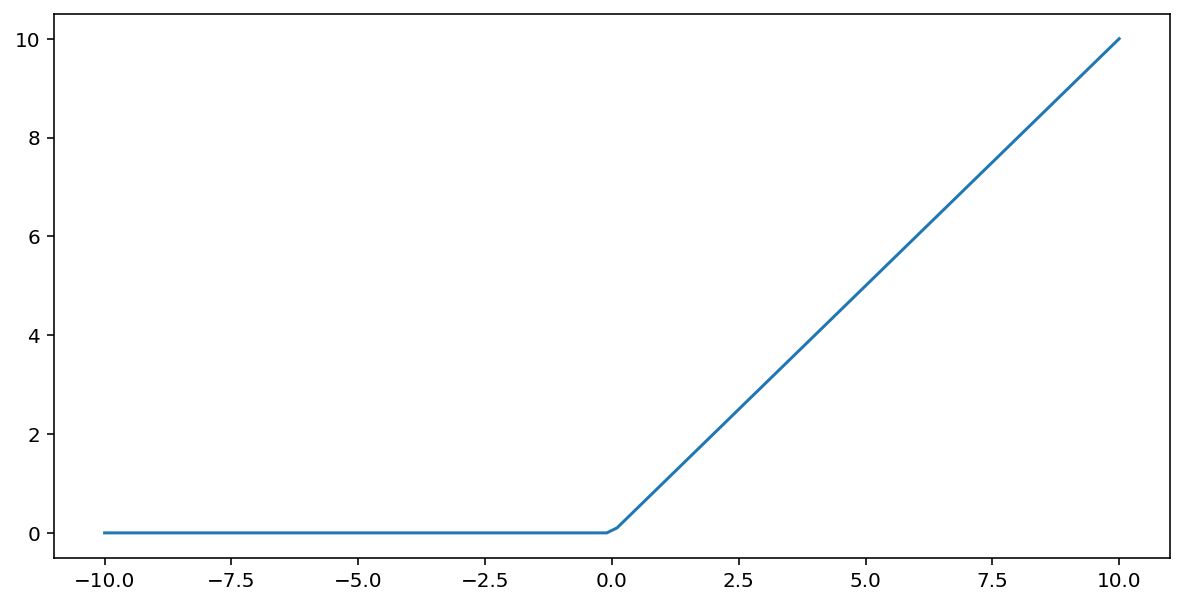
Fungsi aktivasi unit linear terkoreksi (atau ReLU , singkatnya) mengubah output menggunakan algoritma berikut:

  • Jika nilai input $x$ kurang dari 0, kembalikan 0.
  • Jika nilai input $x$ lebih besar dari atau sama dengan 0, kembalikan nilai input tersebut.

ReLU dapat direpresentasikan secara matematis menggunakan fungsi max():

$$F(x)=max(0,x)$$

Berikut adalah grafik fungsi ini:

Gambar 6. Grafik fungsi ReLU: garis horizontal di sepanjang sumbu x dari negatif tak hingga ke 0, yang menjadi garis diagonal naik dan ke kanan dengan kemiringan 1 (y=x) dari 0 hingga tak hingga.
Gambar 6. Grafik fungsi ReLU.

ReLU seringkali bekerja sedikit lebih baik sebagai fungsi aktivasi daripada fungsi halus seperti sigmoid atau tanh, karena kurang rentan terhadap masalah gradien yang menghilang selama pelatihan jaringan saraf . ReLU juga jauh lebih mudah dihitung daripada fungsi-fungsi tersebut.

Fungsi aktivasi lainnya

Dalam praktiknya, fungsi matematika apa pun dapat berfungsi sebagai fungsi aktivasi. Misalkan bahwa \(\sigma\) mewakili fungsi aktivasi kita. Nilai sebuah node dalam jaringan diberikan oleh rumus berikut:

$$\sigma(\boldsymbol w \cdot \boldsymbol x+b)$$

Keras menyediakan dukungan bawaan untuk banyak fungsi aktivasi . Meskipun demikian, kami tetap merekomendasikan untuk memulai dengan ReLU.

Ringkasan

Video berikut ini memberikan rangkuman dari semua yang telah Anda pelajari sejauh ini tentang cara membangun jaringan saraf:

Sekarang model kita memiliki semua komponen standar yang biasanya dimaksud orang ketika mereka merujuk pada jaringan saraf:

  • Sekumpulan node, yang analog dengan neuron, tersusun dalam lapisan-lapisan.
  • Sekumpulan bobot dan bias yang dipelajari yang mewakili koneksi antara setiap lapisan jaringan saraf dan lapisan di bawahnya. Lapisan di bawahnya dapat berupa lapisan jaringan saraf lain, atau jenis lapisan lainnya.
  • Fungsi aktivasi yang mengubah output dari setiap node dalam suatu layer. Layer yang berbeda mungkin memiliki fungsi aktivasi yang berbeda.

Namun perlu dicatat: jaringan saraf tidak selalu lebih baik daripada persilangan fitur, tetapi jaringan saraf menawarkan alternatif fleksibel yang bekerja dengan baik dalam banyak kasus.

Sebelumnya
Node dan lapisan tersembunyi (15 mnt)
Berikutnya
Pelatihan menggunakan backpropagation (10 mnt)