Эмбеддинг – это векторное представление данных в пространстве эмбеддинга. Упрощенно говоря, модель находит возможные эмбеддинги, проецируя высокоразмерное пространство исходных векторов данных на низкоразмерное. Больше узнать о разнице между высоко- и низкоразмерными данными можно в модуле Категориальные данные.
Эмбеддинги упрощают процесс машинного обучения на больших признаковых описаниях, таких как разреженные векторы, представляющие блюда. Об этих векторах мы говорили в предыдущем разделе. Иногда взаимное положение объектов в пространстве эмбеддинга зависит от возможных семантических отношений, но зачастую человеку трудно понять, как определяется низкоразмерное пространство и относительные положения в нем, а также разобраться в полученных эмбеддингах.
Чтобы дать некоторое представление о том, как эмбеддинги выражают информацию, рассмотрим набор блюд (hot dog, pizza, salad, shawarma и borscht), размещенных в ряд на шкале от "меньше всего похоже на бутерброд" до "больше всего похоже на бутерброд". Такое одномерное представление станет условной мерой "бутербродности".
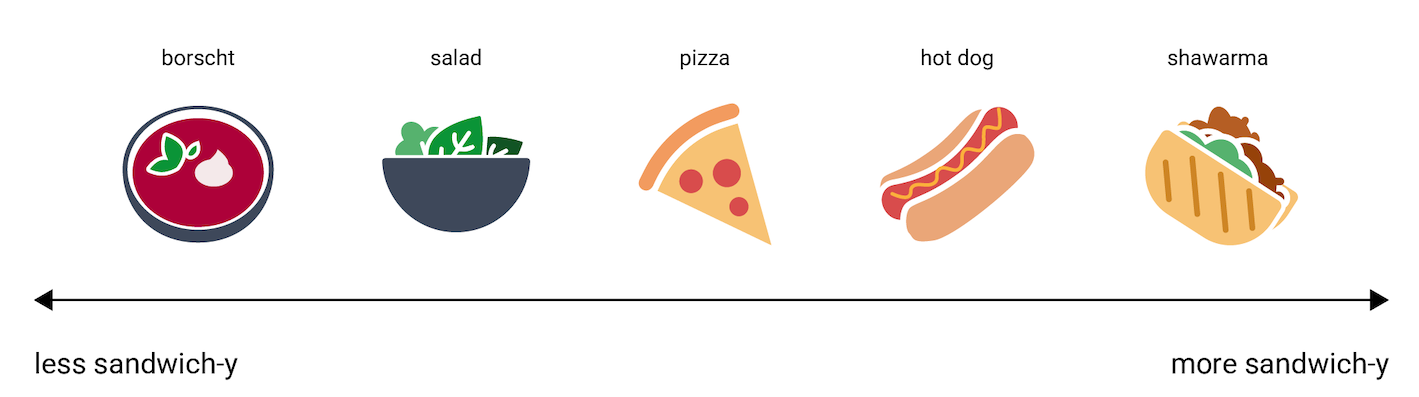
Где на этой шкале окажется блюдо apple strudel? Вероятно, его можно разместить между hot dog и shawarma. Однако у блюда apple strudel также будет дополнительная характеристика сладость или десертность, отличающая его от остальных в этом ряду.
На следующей иллюстрации добавлено измерение "десертность".
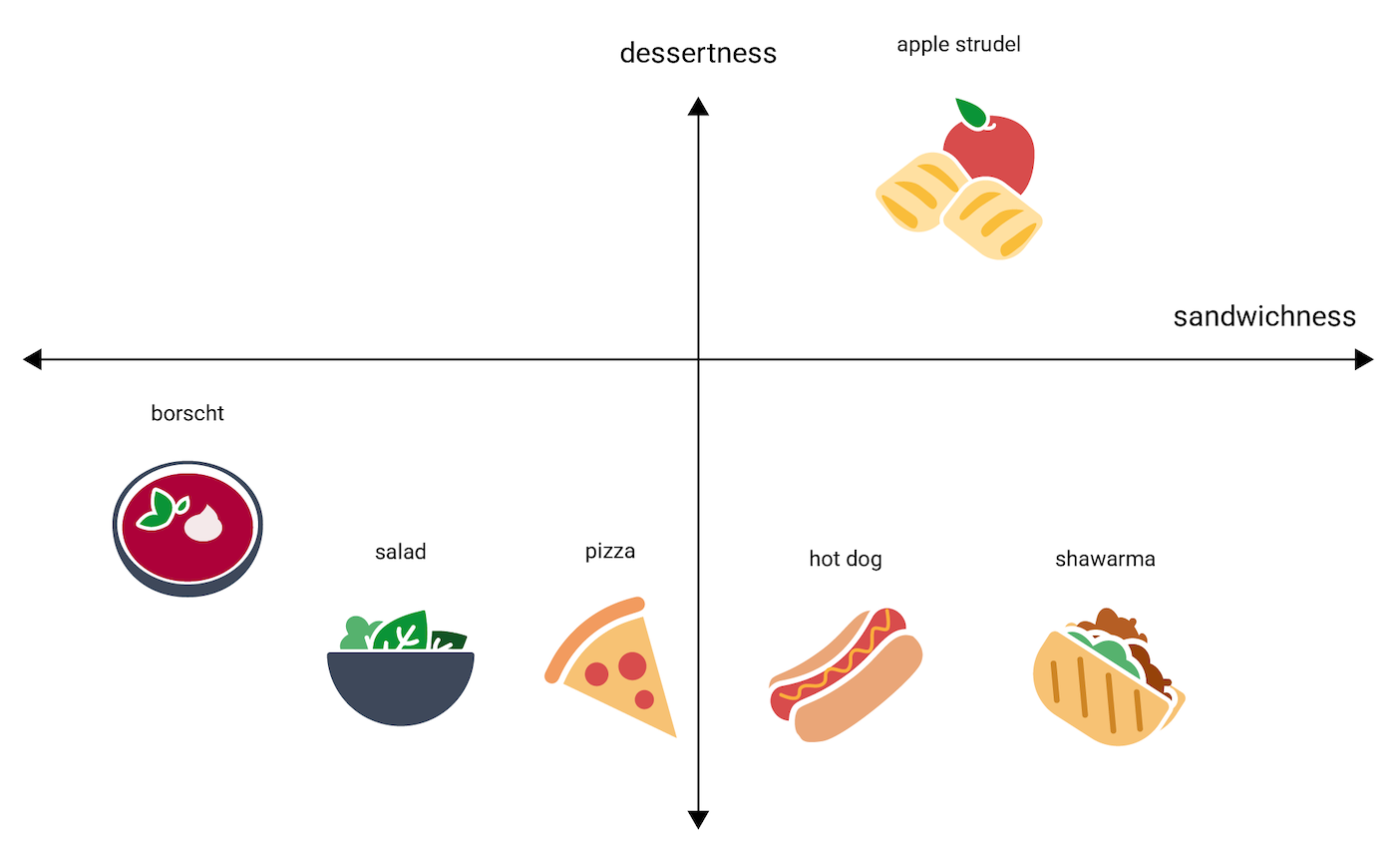
Эмбеддинг представляет каждый объект в n-мерном пространстве с помощью n чисел с плавающей запятой (обычно в диапазоне от −1 до 1 или от 0 до 1). В одномерном пространстве на рисунке 3 каждое блюдо представлено единственной координатой, в то время как в двумерном пространстве на рисунке 4 – уже двумя. На рисунке 4 блюдо apple strudel с координатами (0,5, 0,3) находится в правом верхнем квадранте графика, а блюдо hot dog с координатами (0,2, −0,5) – в правом нижнем.
Расстояние между двумя объектами в эмбеддинге можно рассчитать математически. Оно интерпретируется как мера их относительной схожести. Объекты, расположенные недалеко друг от друга, например shawarma и hot dog на рисунке 4, теснее взаимосвязаны в представлении данных модели, чем те, что разнесены дальше, например apple strudel и borscht.
Заметьте, что в двухмерном пространстве на рисунке 4 apple strudel находится значительно дальше от shawarma и hot dog, чем в одномерном. Это интуитивно понятно: hot dog и shawarma более схожи между собой, чем любое из них похоже на apple strudel.
Теперь рассмотрим borscht. Это суп, и он гораздо более жидкий, чем остальные блюда. Чтобы отразить это свойство, потребуется третье измерение, жидкостность. Следовательно, можно создать следующую трехмерную визуализацию.
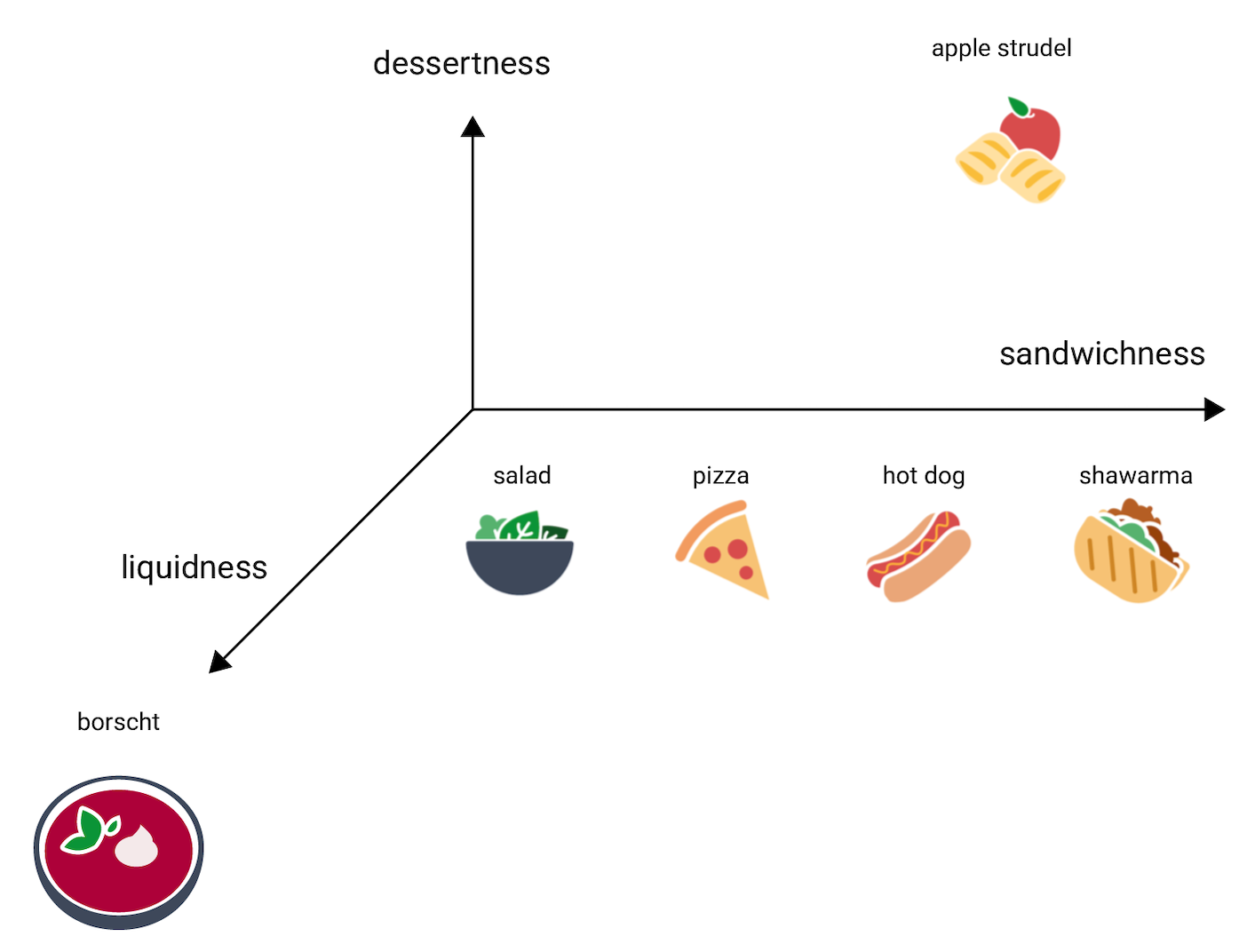
Где в этом трехмерном пространстве окажется блюдо tangyuan? В нем сироп, что делает его похожим на borscht. В то же время это сладкий десерт, как apple strudel, и совершенно очевидно, что это не бутерброд. Ниже приведен один из вариантов размещения этого блюда.
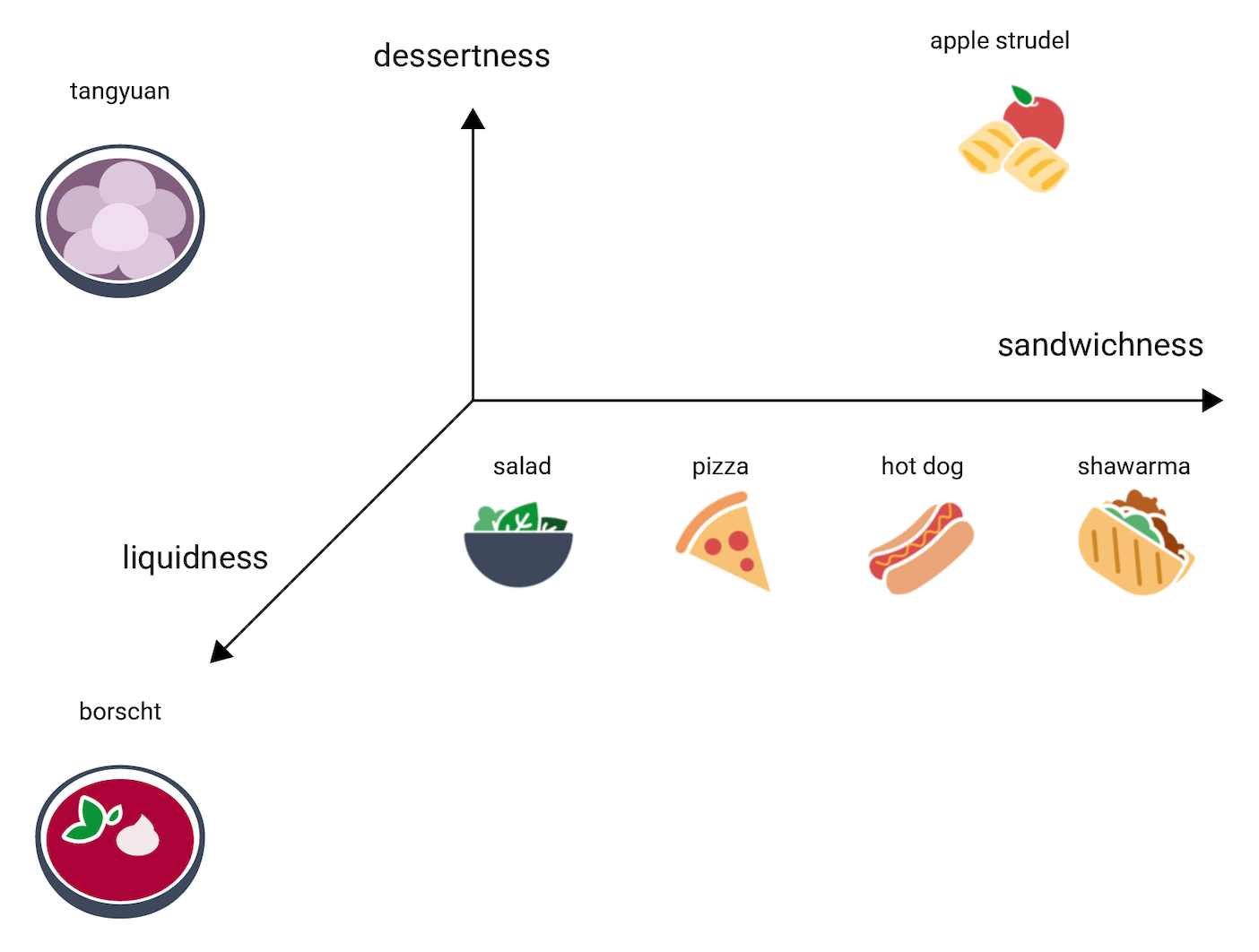
Обратите внимание, как много информации дают эти три измерения. Вы можете добавить дополнительные характеристики, такие как количество мяса в блюде или необходимость его запекания, хотя четвертое, пятое и более высокие измерения трудно визуализировать.
Пространства эмбеддинга в реальном мире
В реальности пространства эмбеддинга имеют d измерений, где d значительно больше трех, но меньше, чем размерность данных. При этом отношения между элементами модели не обязательно столь интуитивно понятны, как в приведенных выше примерах. Так, для эмбеддингов слов d часто равняется 256, 512 или 10241.
На практике при машинном обучении обычно определяется задача и количество измерений для создания эмбеддингов. Затем модель пытается разместить имеющиеся примеры как можно ближе друг к другу в пространстве эмбеддинга с указанным количеством измерений или сама подстраивает это количество, если d не фиксировано. Эти измерения редко бывают так же понятны, как "десертность" или "жидкостность". Далеко не во всех случаях можно понять, какие характеристики они представляют.
Обычно при выполнении разных задач получаются разные эмбеддинги. Например, эмбеддинги для модели, которая определяет, насколько блюда могут считаться вегетарианскими, будут отличаться от эмбеддингов для модели, предлагающей блюда в зависимости от времени суток или сезона. Так, "овсянка" и "колбаса для завтрака" будут, вероятно, ближе друг к другу в пространстве эмбеддинга второй модели, чем первой.
Статические эмбеддинги
В целом эмбеддинги зависят от задачи, но здесь будет уместно остановиться на такой универсальной задаче, как предсказание контекста для слова. В моделях, которые обучены выдавать такие предсказания, предполагается, что слова, которые используются в схожих контекстах, семантически связаны. Предположим, что в данных для обучения есть фразы "Они спустились в Гранд-Каньон верхом на осле" и "Они спустились в каньон верхом на лошади". Модель определит контексты для слов "лошадь" и "осел" как схожие. Эмбеддинги, созданные на основании семантического сходства, хорошо подходят для многих общих лингвистических задач.
Хотя модель word2vec создана уже достаточно давно и сегодня используется редко, она вполне может использоваться в качестве иллюстрации. word2vec обучается на массиве документов и для каждого слова выдает один универсальный эмбеддинг. Когда у слова или элемента данных есть только один эмбеддинг, оно называется статическим. В ролике ниже представлен процесс обучения word2vec в упрощенном виде.
Как показывают исследования, статические эмбеддинги кодируют некоторый объем семантической информации, в частности в форме отношений между словами. То есть слова, которые используются в схожих контекстах, будут находиться рядом в пространстве эмбеддинга. Сами векторы эмбеддингов будут зависеть от массива данных для обучения. Больше информации по этой теме можно найти в работе T. Mikolov et al (2013), Efficient estimation of word representations in vector space.
-
François Chollet, Deep Learning with Python (Shelter Island, NY: Manning, 2017), 6.1.2. ↩