การจัดประเภท: ROC และ AUC

ส่วนก่อนหน้านี้แสดงชุดเมตริกโมเดลที่คำนวณทั้งหมดที่ค่าเกณฑ์การจัดประเภทเดียว แต่หากต้องการประเมินคุณภาพของโมเดลตามเกณฑ์ที่เป็นไปได้ทั้งหมด คุณต้องใช้เครื่องมืออื่น

เส้นโค้ง Receiver Operating Characteristic (ROC)

เส้นโค้ง ROC คือการแสดงภาพประสิทธิภาพของโมเดลในเกณฑ์ทั้งหมด ชื่อแบบยาวคือ Receiver Operating Characteristic (ROC) ซึ่งมาจากการตรวจจับเรดาร์ในสมัยสงครามโลกครั้งที่ 2

เส้นโค้ง ROC วาดขึ้นโดยคํานวณอัตราผลบวกจริง (TPR) และอัตราผลบวกลวง (FPR) ที่เกณฑ์ที่เป็นไปได้ทั้งหมด (ในทางปฏิบัติคือที่ช่วงเวลาที่เลือก) จากนั้นจึงสร้างกราฟ TPR เทียบกับ FPR โมเดลที่สมบูรณ์แบบซึ่งที่เกณฑ์หนึ่งๆ มี TPR เท่ากับ 1.0 และ FPR เท่ากับ 0.0 จะแสดงได้ด้วยจุดที่ (0, 1) หากไม่สนใจเกณฑ์อื่นๆ ทั้งหมด หรือจะแสดงด้วยข้อมูลต่อไปนี้ก็ได้

รูปที่ 1 ROC และ AUC ของโมเดลสมมติที่สมบูรณ์แบบ

พื้นที่ใต้เส้นโค้ง (AUC)

พื้นที่ใต้กราฟ ROC (AUC) แสดงถึงแนวโน้มที่โมเดลจะจัดอันดับตัวอย่างเชิงบวกสูงกว่าตัวอย่างเชิงลบ หากได้รับตัวอย่างเชิงบวกและเชิงลบที่เลือกแบบสุ่ม

โมเดลที่สมบูรณ์แบบด้านบนซึ่งมีสี่เหลี่ยมจัตุรัสที่มีด้านยาว 1 มีพื้นที่ใต้เส้นโค้ง (AUC) เท่ากับ 1.0 ซึ่งหมายความว่ามีความเป็นไปได้ 100% ที่โมเดลจะจัดอันดับตัวอย่างเชิงบวกที่เลือกแบบสุ่มให้สูงกว่าตัวอย่างเชิงลบที่เลือกแบบสุ่มอย่างถูกต้อง กล่าวคือ เมื่อดูการกระจายของจุดข้อมูลด้านล่าง AUC จะแสดงถึงแนวโน้มที่โมเดลจะวางสี่เหลี่ยมจัตุรัสที่เลือกแบบสุ่มไว้ทางด้านขวาของวงกลมที่เลือกแบบสุ่ม โดยไม่ขึ้นอยู่กับตําแหน่งที่ตั้งเกณฑ์

กล่าวอย่างเป็นรูปธรรมคือ ตัวแยกจดหมายขยะที่มี AUC เท่ากับ 1.0 จะกำหนดให้อีเมลขยะแบบสุ่มมีแนวโน้มที่จะเป็นสแปมมากกว่าอีเมลที่ถูกต้องแบบสุ่มเสมอ การจัดประเภทอีเมลแต่ละฉบับจริงจะขึ้นอยู่กับเกณฑ์ที่คุณเลือก

สําหรับตัวแยกประเภทแบบไบนารี โมเดลที่ทํางานได้เหมือนกับการคาดเดาแบบสุ่มหรือการโยนหัวก้อยมี ROC ที่เป็นเส้นทแยงมุมจาก (0,0) ถึง (1,1) AUC มีค่า 0.5 ซึ่งแสดงถึงโอกาส 50% ในการจัดอันดับตัวอย่างเชิงบวกและเชิงลบแบบสุ่มอย่างถูกต้อง

ในตัวอย่างตัวแยกจดหมายขยะ ตัวแยกจดหมายขยะที่มี AUC เท่ากับ 0.5 จะกำหนดให้อีเมลขยะแบบสุ่มมีความน่าจะเป็นสูงกว่าว่าจะเป็นจดหมายขยะมากกว่าอีเมลที่ถูกต้องแบบสุ่มเพียงครึ่งเดียวเท่านั้น

รูปที่ 2 ROC และ AUC ของการเดาแบบสุ่มทั้งหมด

(ไม่บังคับ ขั้นสูง) เส้นโค้ง Precision-Recall

AUC และ ROC เหมาะสําหรับการเปรียบเทียบโมเดลเมื่อชุดข้อมูลมีความสมดุลกันโดยประมาณระหว่างคลาสต่างๆ เมื่อชุดข้อมูลไม่สมดุล เส้นโค้งความแม่นยำและการเรียกคืน (PRC) และพื้นที่ใต้เส้นโค้งเหล่านั้นอาจแสดงภาพประสิทธิภาพของโมเดลแบบเปรียบเทียบได้ดีกว่า เส้นกราฟ Precision-Recall สร้างขึ้นโดยการพล็อตความแม่นยำบนแกน y และความแม่นยำบนแกน x ในทุกเกณฑ์

AUC และ ROC สําหรับการเลือกรูปแบบและเกณฑ์

AUC เป็นค่าการวัดที่มีประโยชน์สําหรับการเปรียบเทียบประสิทธิภาพของโมเดล 2 รูปแบบที่แตกต่างกัน ตราบใดที่ชุดข้อมูลมีความสมดุลโดยประมาณ โดยทั่วไปแล้ว โมเดลที่มีพื้นที่ใต้เส้นโค้งมากกว่าจะดีกว่า

รูปที่ 3 ROC และ AUC ของโมเดลสมมติ 2 รูปแบบ เส้นโค้งทางด้านขวาซึ่งมี AUC มากกว่าแสดงถึงโมเดลที่ดีกว่าของ 2 โมเดล

จุดในเส้นโค้ง ROC ที่ใกล้กับ (0,1) มากที่สุดแสดงถึงช่วงของเกณฑ์ที่มีประสิทธิภาพดีที่สุดสําหรับโมเดลหนึ่งๆ ตามที่เราได้อธิบายไว้ในส่วนเกณฑ์ ตารางความสับสน และการเลือกเมตริกและข้อเสียเปรียบ เกณฑ์ที่คุณเลือกจะขึ้นอยู่กับเมตริกที่มีความสําคัญต่อกรณีการใช้งานหนึ่งๆ มากที่สุด พิจารณาจุด A, B และ C ในแผนภาพต่อไปนี้ ซึ่งแต่ละจุดแสดงถึงเกณฑ์

รูปที่ 4 จุดที่มีป้ายกำกับ 3 จุดแสดงถึงเกณฑ์

หากผลบวกลวง (การแจ้งเตือนที่ผิดพลาด) มีต้นทุนสูง ก็อาจเลือกเกณฑ์ที่ให้ FPR ต่ำลง เช่น เกณฑ์ที่จุด A แม้ว่า TPR จะลดลงก็ตาม ในทางกลับกัน หากผลบวกลวงมีต้นทุนต่ำและผลลบลวง (ผลบวกจริงที่พลาดไป) มีต้นทุนสูง คุณอาจเลือกใช้เกณฑ์ของจุด C ซึ่งเพิ่ม TPR สูงสุด หากต้นทุนใกล้เคียงกัน จุด B อาจให้ความสมดุลที่ดีที่สุดระหว่าง TPR กับ FPR

เส้นโค้ง ROC สำหรับข้อมูลที่เราเห็นก่อนหน้านี้มีดังนี้

แบบฝึกหัด: ทดสอบความเข้าใจ

ในทางปฏิบัติ เส้นโค้ง ROC จะไม่ค่อยสม่ำเสมอเท่ากับภาพประกอบที่แสดงด้านบน โมเดลใดต่อไปนี้ที่แสดงด้วยเส้นโค้ง ROC และ AUC มีประสิทธิภาพดีที่สุด

โมเดลนี้มี AUC สูงสุด ซึ่งสอดคล้องกับประสิทธิภาพที่ดีที่สุด

โมเดลใดต่อไปนี้มีประสิทธิภาพต่ำกว่าโอกาส

รูปแบบนี้มี AUC ต่ำกว่า 0.5 ซึ่งหมายความว่ามีประสิทธิภาพต่ำกว่าโอกาส

โมเดลนี้มีประสิทธิภาพดีกว่าโอกาสเล็กน้อย

รูปแบบนี้ทำงานเหมือนกับโอกาส

นี่เป็นตัวแยกประเภทที่สมบูรณ์แบบสมมติ

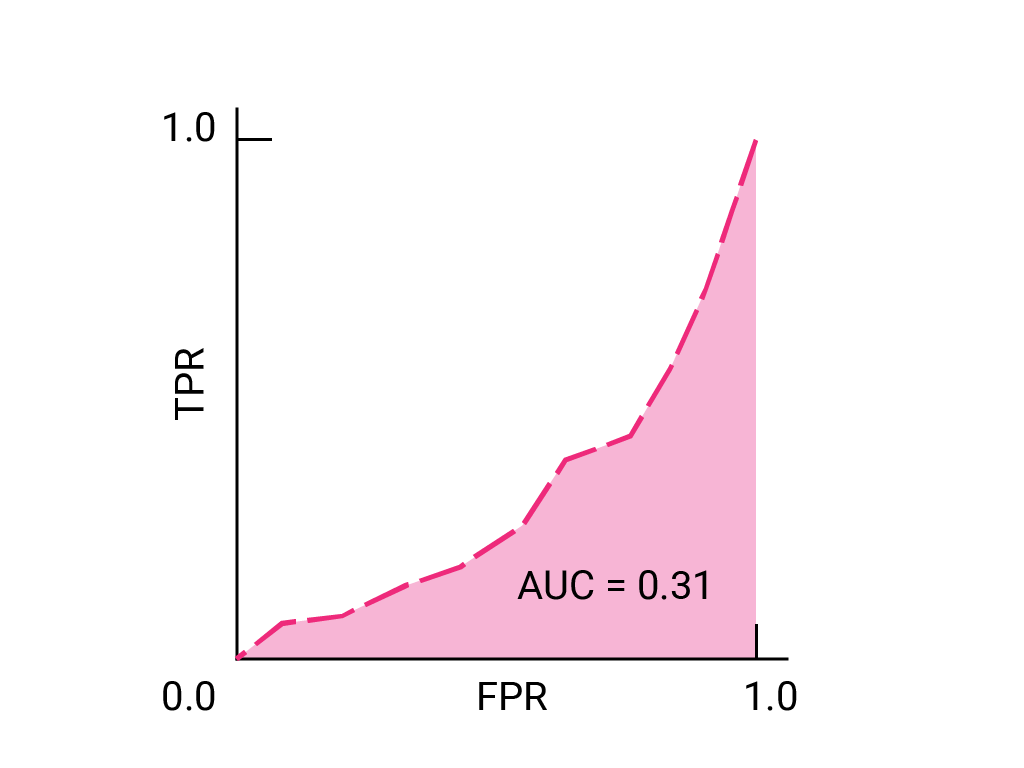
(ไม่บังคับ ขั้นสูง) คำถามพิเศษ

การเปลี่ยนแปลงใดต่อไปนี้ที่ทําได้กับโมเดลที่มีประสิทธิภาพต่ำกว่าโอกาสในคําถามก่อนหน้าเพื่อให้มีประสิทธิภาพดีกว่าโอกาส

เปลี่ยนการคาดการณ์กลับกัน เช่น การคาดการณ์ 1 เปลี่ยนเป็น 0 และการคาดการณ์ 0 เปลี่ยนเป็น 1

หากตัวแยกประเภทแบบไบนารีจัดตัวอย่างไว้ในคลาสที่ไม่ถูกต้องบ่อยกว่าที่ควรจะเป็น การเปลี่ยนป้ายกำกับคลาสจะทำให้การคาดการณ์ดีกว่าที่ควรจะเป็นทันทีโดยไม่ต้องฝึกโมเดลซ้ำ

ให้ระบบคาดการณ์คลาสเชิงลบเสมอ

การดำเนินการนี้อาจปรับปรุงประสิทธิภาพให้ดีขึ้นกว่าโอกาสที่เป็นไปได้หรือไม่ก็ได้ นอกจากนี้ ดังที่ได้กล่าวไว้ในส่วนความแม่นยำ รูปแบบนี้ก็ไม่มีประโยชน์

ให้ระบบคาดการณ์คลาสที่เป็นบวกเสมอ

การดำเนินการนี้อาจปรับปรุงประสิทธิภาพให้ดีขึ้นกว่าโอกาสที่เป็นไปได้หรือไม่ก็ได้ นอกจากนี้ ดังที่ได้กล่าวไว้ในส่วนความแม่นยำ รูปแบบนี้ก็ไม่มีประโยชน์

ลองนึกถึงสถานการณ์ที่ควรอนุญาตให้สแปมบางรายการเข้าถึงกล่องจดหมายมากกว่าที่จะส่งอีเมลที่สำคัญต่อธุรกิจไปยังโฟลเดอร์จดหมายขยะ คุณได้ฝึกจัดประเภทจดหมายขยะสำหรับสถานการณ์นี้ โดยที่คลาสที่เป็นบวกคือจดหมายขยะ และคลาสที่เป็นลบคือไม่ใช่จดหมายขยะ คุณควรเลือกจุดใดต่อไปนี้บนเส้นโค้ง ROC สําหรับตัวแยกประเภท

จุด A

ใน Use Case นี้ คุณควรลดผลบวกลวงให้เหลือน้อยที่สุด แม้ว่าผลบวกจริงจะลดลงด้วยก็ตาม

จุด B

เกณฑ์นี้จะปรับสมดุลระหว่างผลบวกจริงและผลบวกลวง

จุด C

เกณฑ์นี้จะเพิ่มผลบวกจริงให้สูงสุด (แจ้งว่าเป็นจดหมายขยะมากขึ้น) โดยมีผลเสียคือมีจำนวนผลบวกลวงมากขึ้น (มีการแจ้งอีเมลที่ถูกต้องว่าเป็นจดหมายขยะมากขึ้น)

คําสําคัญ:

• พื้นที่ใต้เส้นโค้ง ROC (AUC)
• เส้นโค้ง ROC

ศูนย์ช่วยเหลือ