מילון מונחים בנושא למידת מכונה: מדדים

בדף הזה מופיעים מונחים ממילון המונחים בנושא מדדים. כאן אפשר לראות את כל המונחים במילון המונחים.

A

דיוק

#fundamentals

#Metric

מספר התחזיות הנכונות של הסיווג חלקי המספר הכולל של התחזיות. כלומר:

$$\text{Accuracy} = \frac{\text{correct predictions}} {\text{correct predictions + incorrect predictions }}$$

לדוגמה, למודל שביצע 40 חיזויים נכונים ו-10 חיזויים לא נכונים יהיה דיוק של:

$$\text{Accuracy} = \frac{\text{40}} {\text{40 + 10}} = \text{80%}$$

סיווג בינארי מספק שמות ספציפיים לקטגוריות השונות של תחזיות נכונות ותחזיות שגויות. לכן, הנוסחה לחישוב הדיוק בסיווג בינארי היא:

$$\text{Accuracy} = \frac{\text{TP} + \text{TN}} {\text{TP} + \text{TN} + \text{FP} + \text{FN}}$$

where:‎

• TP הוא מספר החיוביים האמיתיים (תחזיות נכונות).
• TN הוא מספר השליליים האמיתיים (חיזויים נכונים).
• FP הוא מספר החיוביים השגויים (תחזיות שגויות).
• FN הוא מספר התוצאות השליליות השגויות (תחזיות שגויות).

השוו בין דיוק לבין דיוק והחזרה.

כדי לקבל פרטים על רמת הדיוק ועל מערכי נתונים לא מאוזנים לפי סיווג, לוחצים על הסמל.

למרות שמדובר במדד חשוב במצבים מסוימים, במצבים אחרים הוא עלול להטעות מאוד. חשוב לציין שדיוק הוא בדרך כלל מדד לא טוב להערכת מודלים של סיווג שמבצעים עיבוד של מערכי נתונים עם חוסר איזון בין המחלקות.

לדוגמה, נניח שבמאה שנה יורד שלג רק ב-25 ימים בעיר סובטרופית מסוימת. מכיוון שמספר הימים ללא שלג (הסיווג השלילי) גדול בהרבה ממספר הימים עם שלג (הסיווג החיובי), מערך הנתונים של השלג בעיר הזו הוא לא מאוזן. תארו לעצמכם מודל של סיווג בינארי שאמור לחזות אם יירד שלג בכל יום, אבל פשוט חוזה שלא יירד שלג בכל יום. המודל הזה מדויק מאוד אבל אין לו יכולת חיזוי. בטבלה הבאה מסוכמות התוצאות של חיזויים למשך מאה שנה:

קטגוריה	מספר
TP	0
TN	36499
FP	0
FN	25

לכן, רמת הדיוק של המודל הזה היא:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (0 + 36499) / (0 + 36499 + 0 + 25) = 0.9993 = 99.93%

למרות שרמת דיוק של 99.93% נראית מרשימה מאוד, למודל אין יכולת חיזוי.

בדרך כלל, המדדים דיוק והחזרה שימושיים יותר מהמדד דיוק להערכת מודלים שאומנו על מערכי נתונים עם חוסר איזון בין המחלקות.

---

מידע נוסף זמין במאמר סיווג: דיוק, היזכרות, פרסיזיה ומדדים קשורים בסדנה ללמידת מכונה.

השטח מתחת לעקומת ה-PR

#Metric

מידע נוסף על PR AUC (השטח מתחת לעקומת ה-PR)

השטח מתחת לעקומת ה-ROC

#Metric

מידע נוסף על AUC (השטח מתחת לעקומת ROC)

AUC (השטח מתחת לעקומת ROC)

#fundamentals

#Metric

מספר בין 0.0 ל-1.0 שמייצג את היכולת של מודל סיווג בינארי להפריד בין סיווגים חיוביים לבין סיווגים שליליים. ככל שערך ה-AUC קרוב יותר ל-1.0, כך יכולת המודל להפריד בין המחלקות טובה יותר.

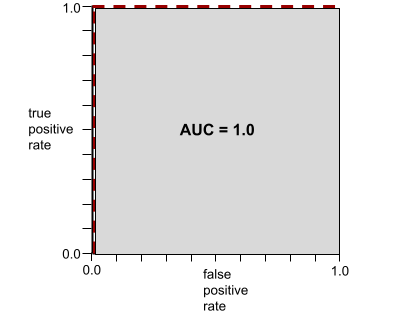
לדוגמה, באיור הבא מוצג מודל סיווג שמפריד בצורה מושלמת בין מחלקות חיוביות (אליפסות ירוקות) לבין מחלקות שליליות (מלבנים סגולים). למודל המושלם הלא-מציאותי הזה יש AUC של 1.0:

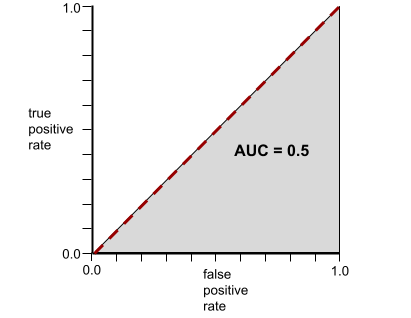
לעומת זאת, באיור הבא מוצגות התוצאות של מודל סיווג שיצר תוצאות אקראיות. המודל הזה כולל AUC של 0.5:

כן, למודל הקודם יש AUC של 0.5, ולא 0.0.

רוב הדגמים נמצאים איפשהו בין שני הקצוות. לדוגמה, המודל הבא מפריד בין ערכים חיוביים לשליליים במידה מסוימת, ולכן ערך ה-AUC שלו הוא בין 0.5 ל-1.0:

המדד AUC מתעלם מכל ערך שתגדירו לסף הסיווג. במקום זאת, AUC מתחשב בכל ספי הסיווג האפשריים.

כדי לקבל מידע על הקשר בין AUC לבין עקומות ROC, לוחצים על הסמל.

הערך AUC מייצג את השטח מתחת לעקומת ROC. לדוגמה, עקומת ה-ROC של מודל שמפריד בצורה מושלמת בין ערכים חיוביים לערכים שליליים נראית כך:

ה-AUC הוא השטח של האזור האפור באיור שלמעלה. במקרה החריג הזה, השטח הוא פשוט האורך של האזור האפור (1.0) כפול הרוחב של האזור האפור (1.0). לכן, המכפלה של 1.0 ו-1.0 היא 1.0 בדיוק, שהוא הציון הכי גבוה שאפשר לקבל ב-AUC.

לעומת זאת, עקומת ה-ROC של מודל סיווג שלא יכול להפריד בין מחלקות בכלל נראית כך. שטח האזור האפור הוא 0.5.

עקומת ROC אופיינית יותר נראית בערך כך:

חישוב השטח מתחת לעקומה הזו באופן ידני הוא תהליך מייגע, ולכן בדרך כלל תוכנה מחשבת את רוב ערכי ה-AUC.

---

אפשר ללחוץ על הסמל כדי לראות הגדרה רשמית יותר של AUC.

המדד AUC הוא ההסתברות שמודל סיווג יהיה בטוח יותר שדוגמה חיובית שנבחרה באופן אקראי היא חיובית, מאשר שדוגמה שלילית שנבחרה באופן אקראי היא חיובית.

---

מידע נוסף זמין במאמר בנושא סיווג: ROC ו-AUC בקורס המקוצר על למידת מכונה.

דיוק ממוצע ב-k

#Metric

מדד לסיכום הביצועים של מודל בהנחיה יחידה שמפיקה תוצאות מדורגות, כמו רשימה ממוספרת של המלצות לספרים. הדיוק הממוצע ב-k הוא, ובכן, הממוצע של ערכי הדיוק ב-k לכל תוצאה רלוונטית. לכן, הנוסחה לחישוב הדיוק הממוצע ב-k היא:

\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]

where:‎

• ‫\(n\) הוא מספר הפריטים הרלוונטיים ברשימה.

השוואה לrecall ב-k.

הערה: המדד 'דיוק ממוצע ב-k' מעריך את הפלט של הנחיה אחת. משתמשים בדיוק ממוצע ב-k כדי להעריך את איכות הפלט של מודל בהנחיות שונות.

הערה: יש אנשים שמקצרים את המונח דיוק ממוצע ב-k לדיוק ממוצע.

לוחצים על הסמל כדי לראות דוגמה

נניח שמודל שפה גדול מקבל את השאילתה הבאה:

List the 6 funniest movies of all time in order.

מודל השפה הגדול מחזיר את הרשימה הבאה:

1. The General
2. Mean Girls
3. Platoon
4. שושבינות
5. האזרח קיין
6. This is Spinal Tap

ארבעה מהסרטים ברשימה שהוחזרה הם מאוד מצחיקים (כלומר, הם רלוונטיים), אבל שני סרטים הם דרמות (לא רלוונטיים). בטבלה הבאה מפורטות התוצאות:

מיקום	סרט	רלוונטי?	Precision at k
1	The General	כן	1.0
2	Mean Girls	כן	1.0
3	Platoon	לא	לא רלוונטי
4	שושבינות	כן	0.75
5	האזרח קיין	לא	לא רלוונטי
6	This is Spinal Tap	כן	0.67

מספר התוצאות הרלוונטיות הוא 4. לכן, אפשר לחשב את הדיוק הממוצע ב-6 באופן הבא:

$${\text{average precision at 6}} = \frac{1}{4} {\text{(1.0 + 1.0 + 0.75 + 0.67)} } $$ $${\text{average precision at 6}} = {\text{~0.85} } $$

---

B

baseline

#Metric

מודל שמשמש כנקודת השוואה לביצועים של מודל אחר (בדרך כלל מודל מורכב יותר). לדוגמה, מודל רגרסיה לוגיסטית יכול לשמש כבסיס טוב למודל עמוק.

במקרה של בעיה מסוימת, ה-Baseline עוזר למפתחי מודלים לכמת את הביצועים המינימליים הצפויים שמודל חדש צריך להשיג כדי שהוא יהיה שימושי.

שאלות בוליאניות (BoolQ)

#Metric

מערך נתונים להערכת היכולת של LLM לענות על שאלות של כן או לא. כל אחת מהבעיות בקבוצת הנתונים כוללת שלושה רכיבים:

• שאילתה
• קטע שממנו אפשר להסיק את התשובה לשאילתה.
• התשובה הנכונה, שהיא כן או לא.

לדוגמה:

• שאילתה: האם יש תחנות כוח גרעיניות במישיגן?
• פסקה: ...שלוש תחנות כוח גרעיניות מספקות למישיגן כ-30% מהחשמל שלה.
• תשובה נכונה: כן

החוקרים אספו את השאלות מתוך שאילתות אנונימיות ומצטברות בחיפוש Google, ואז השתמשו בדפי ויקיפדיה כדי לבסס את המידע.

מידע נוסף זמין במאמר BoolQ: Exploring the Surprising Difficulty of Natural Yes/No Questions.

‫BoolQ הוא רכיב של SuperGLUE ensemble.

BoolQ

#Metric

קיצור של שאלות בוליאניות.

C

CB

#Metric

קיצור של CommitmentBank.

ציון F של N-gram של תווים (ChrF)

#Metric

מדד להערכת מודלים של תרגום אוטומטי. ציון F של N-גרמות של תווים קובע את מידת החפיפה בין N-גרמות בטקסט ההפניה לבין ה-N-גרמות בטקסט שנוצר על ידי מודל ML.

המדד Character N-gram F-score דומה למדדים במשפחות ROUGE ו-BLEU, אבל:

• המדד F-score של N-gram של תווים פועל על N-gram של תווים.
• המדדים ROUGE ו-BLEU פועלים על N-gram של מילים או על אסימונים.

בחירת חלופות סבירות (COPA)

#Metric

מערך נתונים להערכת היכולת של מודל LLM לזהות את התשובה הטובה יותר מבין שתי תשובות חלופיות להנחת יסוד. כל אחת מהבעיות במערך הנתונים מורכבת משלושה רכיבים:

• הנחת יסוד, שהיא בדרך כלל הצהרה שאחריה מופיעה שאלה
• שתי תשובות אפשריות לשאלה שמוצגת בפריט, שאחת מהן נכונה והשנייה לא נכונה
• התשובה הנכונה

לדוגמה:

• הנחת יסוד: הגבר שבר את הבוהן. מה הייתה הסיבה לכך?
• תשובות אפשריות:
  1. הוא קיבל חור בגרב.
  2. הוא הפיל פטיש על הרגל שלו.
• תשובה נכונה: 2

‫COPA הוא רכיב של SuperGLUE ensemble.

CommitmentBank (CB)

#Metric

מערך נתונים להערכת רמת המיומנות של מודל LLM בקביעה אם מחבר הקטע מאמין לסעיף היעד בתוך הקטע. כל רשומה במערך הנתונים מכילה:

• פסקה
• סעיף יעד בתוך הפסקה הזו
• ערך בוליאני שמציין אם מחבר הקטע מאמין שהסעיף

לדוגמה:

• פסקה: איזה כיף לשמוע את ארטמיס צוחקת. היא ילדה כל כך רצינית. לא ידעתי שיש לה חוש הומור.
• סעיף היעד: she had a sense of humor
• ‫Boolean: True, כלומר המחבר מאמין שהסעיף הממוקד

‫CommitmentBank הוא רכיב של SuperGLUE ensemble.

COPA

#Metric

קיצור של בחירת חלופות סבירות.

עלות

#Metric

מילה נרדפת להפסד.

הוגנות קונטרה-פקטואלית

#responsible

#Metric

מדד הוגנות שבודק אם מודל סיווג מפיק את אותה תוצאה עבור אדם מסוים כמו עבור אדם אחר זהה, למעט מאפיינים רגישים מסוימים. הערכה של מודל סיווג מבחינת הוגנות קונטרה-פקטואלית היא שיטה אחת לחשיפת מקורות פוטנציאליים של הטיה במודל.

מידע נוסף זמין במאמרים הבאים:

• הוגנות: הוגנות מנוגדת לעובדות בקורס המקוצר על למידת מכונה.
• When Worlds Collide: Integrating Different Counterfactual Assumptions in Fairness

אנטרופיה צולבת

#Metric

הכללה של Log Loss לבעיות סיווג מרובות מחלקות. האנטרופיה הצולבת מכמתת את ההבדל בין שתי התפלגויות הסתברות. מידע נוסף זמין במאמר בנושא perplexity.

פונקציית התפלגות מצטברת (CDF)

#Metric

פונקציה שמגדירה את התדירות של דגימות שקטנות מערך יעד או שוות לו. לדוגמה, נניח שיש התפלגות נורמלית של ערכים רציפים. פונקציית CDF מראה שכ-50% מהדגימות צריכות להיות קטנות מהממוצע או שוות לו, וכ-84% מהדגימות צריכות להיות קטנות מהממוצע בסטיית תקן אחת או שוות לו.

D

שוויון דמוגרפי

#responsible

#Metric

מדד הוגנות שמתקיים אם תוצאות הסיווג של המודל לא תלויות במאפיין רגיש נתון.

לדוגמה, אם גם אנשי ליליפוט וגם אנשי ברובדינגנאג מגישים בקשה להתקבל לאוניברסיטת גלאבדאבדריב, מתקבלת שוויון דמוגרפי אם אחוז אנשי ליליפוט שהתקבלו זהה לאחוז אנשי ברובדינגנאג שהתקבלו, ללא קשר לשאלה אם קבוצה אחת מוסמכת יותר מהשנייה בממוצע.

ההגדרה הזו שונה מסיכויים שווים ומשוויון הזדמנויות, שמאפשרות לתוצאות הסיווג הכוללות להיות תלויות במאפיינים רגישים, אבל לא מאפשרות לתוצאות הסיווג של תוויות אמת בסיסית מסוימות להיות תלויות במאפיינים רגישים. במאמר "Attacking discrimination with smarter machine learning" (התמודדות עם אפליה באמצעות למידת מכונה חכמה יותר) מוצג תרשים שממחיש את היתרונות והחסרונות של אופטימיזציה להשגת שוויון דמוגרפי.

מידע נוסף זמין במאמר בנושא הוגנות: שוויון דמוגרפי בקורס המקוצר על למידת מכונה.

E

מרחק בין תמונות (EMD)

#Metric

מדד לדמיון היחסי בין שתי התפלגויות. ככל שהמרחק בין המכונות קטן יותר, כך ההתפלגויות דומות יותר.

מרחק עריכה

#Metric

מדד של מידת הדמיון בין שתי מחרוזות טקסט. בלמידת מכונה, מרחק העריכה שימושי מהסיבות הבאות:

• קל לחשב את מרחק העריכה.
• מרחק העריכה יכול להשוות בין שתי מחרוזות שידוע שהן דומות זו לזו.
• מרחק העריכה יכול לקבוע את מידת הדמיון בין מחרוזות שונות למחרוזת נתונה.

יש כמה הגדרות של מרחק עריכה, וכל אחת מהן משתמשת בפעולות שונות על מחרוזות. דוגמה מופיעה במאמר בנושא מרחק לבנשטיין.

פונקציית התפלגות מצטברת אמפירית (eCDF או EDF)

#Metric

פונקציית התפלגות מצטברת שמבוססת על מדידות אמפיריות ממערך נתונים אמיתי. הערך של הפונקציה בכל נקודה לאורך ציר ה-x הוא החלק של התצפיות במערך הנתונים שקטן מהערך שצוין או שווה לו.

אנטרופיה

#df

#Metric

ב תורת המידע, אנטרופיה היא תיאור של מידת חוסר הצפיות של התפלגות הסתברותית. לחלופין, אנטרופיה מוגדרת גם ככמות המידע שכל דוגמה מכילה. הפיזור הוא בעל האנטרופיה הגבוהה ביותר האפשרית כשכל הערכים של משתנה אקראי הם בעלי סבירות שווה.

הנוסחה לחישוב האנטרופיה של קבוצה עם שני ערכים אפשריים, 0 ו-1 (לדוגמה, התוויות בבעיית סיווג בינארי), היא:

  H = -p log p - q log q = -p log p - (1-p) * log (1-p)

where:‎

• ‫H היא האנטרופיה.
• ‫p הוא החלק היחסי של דוגמאות מסוג '1'.
• ‫q הוא החלק של הדוגמאות עם הערך '0'. שימו לב: q = (1 - p)
• הערך log הוא בדרך כלל log₂. במקרה הזה, יחידת האנטרופיה היא ביט.

לדוגמה, נניח את הדברים הבאים:

• ‫100 דוגמאות מכילות את הערך '1'
• ‫300 דוגמאות מכילות את הערך '0'

לכן, ערך האנטרופיה הוא:

• p = 0.25
• q = 0.75
• H = (-0.25)log₂(0.25) - (0.75)log₂(0.75) = 0.81 bits per example

קבוצה מאוזנת לחלוטין (לדוגמה, 200 ערכים של '0' ו-200 ערכים של '1') תהיה בעלת אנטרופיה של 1.0 ביט לכל דוגמה. ככל שקבוצה הופכת לא מאוזנת יותר, האנטרופיה שלה מתקרבת ל-0.0.

בעצי החלטה, האנטרופיה עוזרת לגבש רווח מידע כדי לעזור למפצל לבחור את התנאים במהלך הצמיחה של עץ החלטה לסיווג.

השוואה של האנטרופיה עם:

• מדד גיני לאי-טוהר
• פונקציית האובדן cross-entropy

אנטרופיה נקראת לעיתים קרובות אנטרופיה של שאנון.

מידע נוסף זמין במאמר Exact splitter for binary classification with numerical features בקורס Decision Forests.

שוויון הזדמנויות

#responsible

#Metric

מדד הוגנות להערכת היכולת של המודל לחזות את התוצאה הרצויה באופן שווה לכל הערכים של מאפיין רגיש. במילים אחרות, אם התוצאה הרצויה של מודל היא הסיווג החיובי, המטרה היא ששיעור החיוביים האמיתיים יהיה זהה לכל הקבוצות.

שוויון הזדמנויות קשור לסיכויים שווים, שדורש שגם שיעורי ה-TRUE האמיתיים וגם שיעורי ה-FALSE הכוזבים יהיו זהים בכל הקבוצות.

נניח שבאוניברסיטת גלאבדאבדריב מתקבלים ללימודי מתמטיקה גם ליליפוטים וגם ברובדינגנאגים. בבתי הספר התיכוניים של ליליפוט מוצעת תוכנית לימודים מקיפה של שיעורי מתמטיקה, ורוב התלמידים עומדים בדרישות של התוכנית האוניברסיטאית. בבתי הספר התיכוניים בברובדינגנאג לא מוצעים שיעורי מתמטיקה בכלל, וכתוצאה מכך, הרבה פחות תלמידים עומדים בדרישות. התנאי של שוויון הזדמנויות מתקיים לגבי התווית המועדפת 'התקבל/ה' בהקשר של לאום (ליליפוט או ברובדינגנאג) אם לתלמידים שעומדים בדרישות יש סיכוי שווה להתקבל, בלי קשר ללאום שלהם (ליליפוט או ברובדינגנאג).

לדוגמה, נניח ש-100 אנשים מליליפוט ו-100 אנשים מברובדינגנאג הגישו בקשה להתקבל לאוניברסיטת גלובדאבדריב, וההחלטות לגבי הקבלה מתקבלות באופן הבא:

טבלה 1. מועמדים קטנים מאוד (90% מהם עומדים בדרישות)

	כשירים	לא מתאים
התקבל	45	3
נדחה	45	7
סה"כ	90	10
אחוז הסטודנטים שעומדים בדרישות והתקבלו: 45/90 = 50% אחוז הסטודנטים שלא עומדים בדרישות ונדחו: 7/10 = 70% האחוז הכולל של סטודנטים מליליפוט שהתקבלו: (45+3)/100 = 48%

 

טבלה 2. מועמדים גדולים מאוד (10% כשירים):

	כשירים	לא מתאים
התקבל	5	9
נדחה	5	81
סה"כ	10	90
אחוז הסטודנטים שעומדים בדרישות שהתקבלו: 5/10 = 50% אחוז הסטודנטים שלא עומדים בדרישות שנדחו: 81/90 = 90% אחוז הסטודנטים הכולל מ-Brobdingnag שהתקבלו: (5+9)/100 = 14%

הדוגמאות הקודמות עומדות בדרישה לשוויון הזדמנויות לקבלה של תלמידים שעומדים בדרישות, כי גם לליליפוטים וגם לברובדינגנאגים שעומדים בדרישות יש סיכוי של 50% להתקבל.

למרות שהשוויון בהזדמנויות מתקיים, שני מדדי ההוגנות הבאים לא מתקיימים:

• שוויון דמוגרפי: שיעורי הקבלה של ליליפוטים ושל ברובדינגנאגים לאוניברסיטה שונים; 48% מהסטודנטים הליליפוטים מתקבלים, אבל רק 14% מהסטודנטים הברובדינגנאגים מתקבלים.
• סיכויים שווים: לתלמידים זכאים מליליפוט ומברובדינגנאג יש סיכוי שווה להתקבל, אבל התנאי הנוסף שלפיו לתלמידים לא זכאים מליליפוט ומברובדינגנאג יש סיכוי שווה להידחות לא מתקיים. שיעור הדחייה של ליליפוטים לא מוסמכים הוא 70%, לעומת 90% של ברובדינגנאגים לא מוסמכים.

מידע נוסף זמין במאמר הוגנות: שוויון הזדמנויות בקורס Machine Learning Crash Course.

הסתברות שווה

#responsible

#Metric

מדד הוגנות שנועד להעריך אם מודל חוזה תוצאות באותה רמת דיוק לכל הערכים של מאפיין רגיש ביחס לסיווג החיובי ולסיווג השלילי – ולא רק ביחס לסיווג אחד. במילים אחרות, גם שיעור החיוביים האמיתיים וגם שיעור השליליים הכוזבים צריכים להיות זהים בכל הקבוצות.

הסיכויים שווים קשורים לשוויון הזדמנויות, שמתמקד רק בשיעורי השגיאות עבור סיווג יחיד (חיובי או שלילי).

לדוגמה, נניח שאוניברסיטת גלאבדאבדריב מקבלת לתוכנית לימודים קפדנית במתמטיקה גם ליליפוטים וגם ברובדינגנאגים. בתי הספר התיכוניים של ליליפוט מציעים תוכנית לימודים מקיפה של שיעורי מתמטיקה, ורוב התלמידים עומדים בדרישות של התוכנית האוניברסיטאית. בבתי הספר התיכוניים בברובדינגנאג לא מוצעים שיעורי מתמטיקה בכלל, וכתוצאה מכך, הרבה פחות תלמידים עומדים בדרישות. הקריטריון של סיכויים שווים מתקיים אם הסיכוי של מועמד מתאים להתקבל לתוכנית שווה לסיכוי של מועמד מתאים אחר להתקבל לתוכנית, בלי קשר לגודל שלו (ליליפוט או ברובדינגנאג), והסיכוי של מועמד לא מתאים להידחות שווה לסיכוי של מועמד לא מתאים אחר להידחות.

נניח ש-100 אנשים מליליפוט ו-100 אנשים מברובדינגנאג מגישים בקשה להתקבל לאוניברסיטת גלובדאבדריב, והחלטות הקבלה מתקבלות באופן הבא:

טבלה 3. מועמדים קטנים מאוד (90% מהם עומדים בדרישות)

	כשירים	לא מתאים
התקבל	45	2
נדחה	45	8
סה"כ	90	10
אחוז התלמידים שעומדים בדרישות והתקבלו: 45/90 = 50% אחוז התלמידים שלא עומדים בדרישות ונדחו: 8/10 = 80% האחוז הכולל של תלמידי ליליפוט שהתקבלו: (45+2)/100 = 47%

 

טבלה 4. מועמדים גדולים מאוד (10% כשירים):

	כשירים	לא מתאים
התקבל	5	18
נדחה	5	72
סה"כ	10	90
אחוז הסטודנטים שעומדים בדרישות והתקבלו: 5/10 = 50% אחוז הסטודנטים שלא עומדים בדרישות ונדחו: 72/90 = 80% אחוז הסטודנטים הכולל מברובדינגנאג שהתקבלו: (5+18)/100 = 23%

ההגדרה 'סיכויים שווים' מתקיימת כי לסטודנטים כשירים מליליפוט ומברובדינגנאג יש סיכוי של 50% להתקבל, ולסטודנטים לא כשירים מליליפוט ומברובדינגנאג יש סיכוי של 80% להידחות.

הערה: למרות שהתנאי של הסתברות שווה מתקיים כאן, התנאי של שוויון דמוגרפי לא מתקיים. סטודנטים מליליפוט ומברובדינגנאג מתקבלים לאוניברסיטת גלאבדובדריב בשיעורים שונים: 47% מהסטודנטים מליליפוט מתקבלים, ו-23% מהסטודנטים מברובדינגנאג מתקבלים.

ההגדרה הפורמלית של סיכויים שווים מופיעה במאמר "Equality of Opportunity in Supervised Learning" (שוויון הזדמנויות בלמידה מפוקחת) באופן הבא: "הערך החזוי Ŷ מקיים סיכויים שווים ביחס לתכונה המוגנת A ולתוצאה Y אם Ŷ ו-A הם בלתי תלויים, בהינתן Y".

הערה: כדאי להשוות בין הסיכויים השווים לבין המדד המקל יותר שוויון הזדמנויות.

evals

#generativeAI

#Metric

משמש בעיקר כקיצור להערכות של מודלים גדולים של שפה. באופן כללי, evals הוא קיצור לכל סוג של הערכה.

הערכה

#generativeAI

#Metric

התהליך של מדידת האיכות של מודל או השוואה בין מודלים שונים.

כדי להעריך מודל של למידת מכונה מבוקרת, בדרך כלל משווים אותו לקבוצת נתונים לתיקוף ולקבוצת נתונים לבדיקה. הערכה של מודל שפה גדול כוללת בדרך כלל הערכות רחבות יותר של איכות ובטיחות.

התאמה מדויקת

#Metric

מדד של הכול או כלום, שבו הפלט של המודל תואם לאמת הקרקע או לטקסט ההפניה בדיוק או שלא תואם בכלל. לדוגמה, אם אמת הקרקע היא orange, הפלט היחיד של המודל שעומד בדרישות של התאמה מדויקת הוא orange.

התאמה מדויקת יכולה גם להעריך מודלים שהפלט שלהם הוא רצף (רשימה מדורגת של פריטים). באופן כללי, התאמה מדויקת מחייבת שהרשימה המדורגת שנוצרה תהיה זהה לאמת הקרקע; כלומר, כל פריט בשתי הרשימות צריך להיות באותו סדר. עם זאת, אם אמת קרקע מורכבת מכמה רצפים נכונים, התאמה מדויקת דורשת רק שהפלט של המודל יתאים לאחד מהרצפים הנכונים.

סיכום קיצוני (xsum)

#Metric

מערך נתונים להערכת היכולת של LLM לסכם מסמך יחיד. כל רשומה במערך הנתונים כוללת:

• מסמך שנכתב על ידי British Broadcasting Corporation ‏ (BBC).
• סיכום של המסמך במשפט אחד.

פרטים נוספים זמינים במאמר Don't Give Me the Details, Just the Summary!‎ Topic-Aware Convolutional Neural Networks for Extreme Summarization.

F

F₁

#Metric

מדד סיווג בינארי מסכם שמסתמך על דיוק וגם על היזכרות. זו הנוסחה:

$$F{_1} = \frac{\text{2 * precision * recall}} {\text{precision + recall}}$$

אפשר ללחוץ על הסמל כדי לראות דוגמאות.

נניח שערכי הדיוק וההחזרה הם:

• precision = 0.6
• recall = 0.4

כך מחשבים את F₁:

$$F{_1} = \frac{\text{2 * 0.6 * 0.4}} {\text{0.6 + 0.4}} = 0.48$$

כשערכי הדיוק וההחזרה דומים למדי (כמו בדוגמה הקודמת), F₁ קרוב לממוצע שלהם. אם יש הבדל משמעותי בין הדיוק לבין ההחזרה, ערך ה-F₁ יהיה קרוב יותר לערך הנמוך. לדוגמה:

• precision = 0.9
• recall = 0.1

$$F{_1} = \frac{\text{2 * 0.9 * 0.1}} {\text{0.9 + 0.1}} = 0.18$$

---

מדד הוגנות

#responsible

#Metric

הגדרה מתמטית של 'הוגנות' שאפשר למדוד. דוגמאות למדדי הוגנות הכי רווחיים:

• equalized odds
• שוויון חיזוי
• הוגנות קונטרה-פקטואלית
• שוויון דמוגרפי

הרבה מדדים של הוגנות הם בלעדיים הדדית. אפשר לעיין באי-התאמה של מדדים של הוגנות.

FALSE שלילי (FN)

#fundamentals

#Metric

דוגמה שבה המודל מנבא בטעות את הסיווג השלילי. לדוגמה, המודל חוזה שהודעת אימייל מסוימת אינה ספאם (הסיווג השלילי), אבל הודעת האימייל הזו היא למעשה ספאם.

שיעור השליליים השגויים

#Metric

החלק היחסי של דוגמאות חיוביות אמיתיות שהמודל טעה לגביהן וחיזוי שהוא שייך לסיווג השלילי. הנוסחה הבאה משמשת לחישוב שיעור התוצאות השליליות השגויות:

$$\text{false negative rate} = \frac{\text{false negatives}}{\text{false negatives} + \text{true positives}}$$

מידע נוסף זמין במאמר ערכי סף ומטריצת בלבול בקורס המקוצר על למידת מכונה.

FALSE חיובי שגוי (FP)

#fundamentals

#Metric

דוגמה שבה המודל חוזה בטעות את הסיווג החיובי. לדוגמה, המודל חוזה שהודעת אימייל מסוימת היא ספאם (הסיווג החיובי), אבל הודעת האימייל הזו לא ספאם בפועל.

מידע נוסף זמין במאמר ערכי סף ומטריצת בלבול בקורס המקוצר על למידת מכונה.

שיעור התוצאות החיוביות השגויות (FPR)

#fundamentals

#Metric

השיעור של הדוגמאות השליליות בפועל שהמודל טעה בהן וניבא את הסיווג החיובי. הנוסחה הבאה משמשת לחישוב שיעור התוצאות החיוביות הכוזבות:

$$\text{false positive rate} = \frac{\text{false positives}}{\text{false positives} + \text{true negatives}}$$

שיעור התוצאות החיוביות השגויות הוא ציר ה-X בעקומת ROC.

מידע נוסף זמין במאמר בנושא סיווג: ROC ו-AUC בקורס המקוצר על למידת מכונה.

חשיבות התכונות

#df

#Metric

מילה נרדפת למונח חשיבות משתנים.

מודל בסיס

#generativeAI

#Metric

מודל שעבר אימון מראש גדול מאוד שאומן על קבוצת נתונים לאימון עצומה ומגוונת. מודל בסיס יכול לבצע את שתי הפעולות הבאות:

• להגיב בצורה טובה למגוון רחב של בקשות.
• לשמש כמודל בסיסי לכוונון עדין נוסף או להתאמה אישית אחרת.

במילים אחרות, מודל בסיסי כבר מסוגל לבצע משימות רבות באופן כללי, אבל אפשר להתאים אותו עוד יותר כדי שיהיה שימושי יותר למשימה ספציפית.

חלק יחסי של הצלחות

#generativeAI

#Metric

מדד להערכת הטקסט שנוצר על ידי מודל ML. המדד 'חלק ההצלחות' הוא מספר הפלט של הטקסט שנוצר בהצלחה חלקי המספר הכולל של פלט הטקסט שנוצר. לדוגמה, אם מודל שפה גדול יצר 10 בלוקים של קוד, וחמישה מהם היו מוצלחים, אז שיעור ההצלחה יהיה 50%.

למרות שהמדד 'שיעור ההצלחות' שימושי ברוב התחומים בסטטיסטיקה, בלמידת מכונה הוא שימושי בעיקר למדידת משימות שניתן לאמת, כמו יצירת קוד או בעיות מתמטיות.

G

gini impurity

#df

#Metric

מדד שדומה לאנטרופיה. מפצלים משתמשים בערכים שנגזרים מאי-טוהר גיני או מאנטרופיה כדי ליצור תנאים לסיווג עצי החלטה. הרווח במידע נגזר מאנטרופיה. אין מונח מקביל שמקובל באופן אוניברסלי למדד שנגזר מאי-טוהר של גיני. עם זאת, המדד הזה, שאין לו שם, חשוב בדיוק כמו מדד הרווח במידע.

המדד הזה נקרא גם מדד ג'יני או פשוט ג'יני.

כדי לראות פרטים מתמטיים על מדד Gini impurity, לוחצים על הסמל.

טומאת גיני היא ההסתברות לסיווג שגוי של נתון חדש שנלקח מאותה התפלגות. הטומאה של גיני בקבוצה עם שני ערכים אפשריים, 0 ו-1 (לדוגמה, התוויות בבעיה של סיווג בינארי), מחושבת לפי הנוסחה הבאה:

   I = 1 - (p² + q²) = 1 - (p² + (1-p)²)

where:‎

• ‫I הוא מדד טוהר גיני.
• ‫p הוא החלק היחסי של דוגמאות מסוג '1'.
• ‫q הוא החלק של הדוגמאות עם הערך '0'. שימו לב ש-q = 1-p

לדוגמה, נניח שיש לכם את קבוצת הנתונים הבאה:

• ‫100 תוויות (0.25 ממערך הנתונים) מכילות את הערך '1'
• ‫300 תוויות (0.75 ממערך הנתונים) מכילות את הערך '0'

לכן, מדד ה-Gini impurity הוא:

• p = 0.25
• q = 0.75
• I = 1 - (0.25² + 0.75²) = 0.375

לכן, לתווית אקראית מאותו מערך נתונים יש סיכוי של 37.5% לסיווג שגוי, וסיכוי של 62.5% לסיווג נכון.

תווית מאוזנת לחלוטין (לדוגמה, 200 תוויות עם הערך 0 ו-200 תוויות עם הערך 1) תהיה בעלת מדד Gini impurity של 0.5. תווית לא מאוזנת מאוד תהיה בעלת טוהר גיני קרוב ל-0.0.

---

H

אובדן ציר

#Metric

משפחה של פונקציות loss לסיווג שנועדו למצוא את גבול ההחלטה במרחק הכי גדול מכל דוגמה לאימון, וכך למקסם את השוליים בין הדוגמאות לבין הגבול. ב-KSVM נעשה שימוש בפונקציית הפסד ציר (או בפונקציה קשורה, כמו פונקציית הפסד ציר בריבוע). בסיווג בינארי, פונקציית ההפסד של הציר מוגדרת כך:

$$\text{loss} = \text{max}(0, 1 - (y * y'))$$

כאשר y היא התווית האמיתית, -1 או +1, ו-y' הוא הפלט הגולמי של מודל הסיווג:

$$y' = b + w_1x_1 + w_2x_2 + … w_nx_n$$

לכן, תרשים של hinge loss לעומת (y * y') נראה כך:

I

אי התאמה בין מדדי הוגנות

#responsible

#Metric

הרעיון שלפיו חלק מהמושגים של הוגנות לא תואמים זה לזה ולא ניתן לספק אותם בו-זמנית. לכן, אין מדד אוניברסלי יחיד לכמותיות של הוגנות שאפשר להחיל על כל בעיות ה-ML.

יכול להיות שזה נשמע מייאש, אבל חוסר התאמה של מדדי הוגנות לא אומר שהמאמצים להשגת הוגנות הם חסרי תועלת. במקום זאת, הוא מציע להגדיר את ההוגנות בהקשר של בעיה נתונה של למידת מכונה, במטרה למנוע נזקים שספציפיים לתרחישי השימוש שלה.

במאמר "On the (im)possibility of fairness" יש דיון מפורט יותר על חוסר התאימות של מדדי הוגנות.

הוגנות אישית

#responsible

#Metric

מדד הוגנות שבודק אם אנשים דומים מסווגים באופן דומה. לדוגמה, יכול להיות שבאקדמיה מסוימת ירצו להבטיח הוגנות אינדיבידואלית, כלומר ששני תלמידים עם ציונים זהים במבחנים סטנדרטיים יקבלו סיכוי שווה להתקבל למוסד.

חשוב לזכור שההוגנות האישית תלויה לחלוטין בהגדרה של 'דמיון' (במקרה הזה, ציונים במבחנים וציונים בלימודים), ויש סיכון ליצירת בעיות חדשות של הוגנות אם מדד הדמיון לא כולל מידע חשוב (כמו רמת הקושי של תוכנית הלימודים של התלמיד).

במאמר "הוגנות באמצעות מודעות" מופיע דיון מפורט יותר בנושא ההוגנות האישית.

הרווח ממידע

#df

#Metric

ביערות החלטה, ההפרש בין האנטרופיה של צומת לבין הסכום המשוקלל (לפי מספר הדוגמאות) של האנטרופיה של צמתי הצאצאים שלה. האנטרופיה של צומת היא האנטרופיה של הדוגמאות בצומת הזה.

לדוגמה, נבחן את ערכי האנטרופיה הבאים:

• האנטרופיה של צומת ההורה = 0.6
• האנטרופיה של צומת משני אחד עם 16 דוגמאות רלוונטיות = 0.2
• אנטרופיה של צומת צאצא אחר עם 24 דוגמאות רלוונטיות = 0.1

לכן, 40% מהדוגמאות נמצאות בצומת צאצא אחד ו-60% נמצאות בצומת הצאצא השני. לכן:

• סכום האנטרופיה המשוקלל של צומתי הצאצא = (‎0.4 * 0.2) + (‎0.6 * 0.1) = 0.14

לכן, הרווח מהמידע הוא:

• הרווח במידע = האנטרופיה של צומת האב – סכום האנטרופיה המשוקלל של צמתי הבן
• הרווח במידע = 0.6 – 0.14 = 0.46

רוב המספקים מנסים ליצור תנאים שממקסמים את הרווח מהמידע.

הסכמה בין מעריכים

#Metric

מדד שמשקף את מידת ההסכמה בין בודקים אנושיים במהלך ביצוע משימה. אם יש חוסר הסכמה בין הבודקים, יכול להיות שצריך לשפר את ההוראות למשימה. נקרא גם הסכמה בין מבארים או מהימנות בין מעריכים. ראו גם את קאפה של כהן, שהוא אחד ממדדי ההסכמה הפופולריים ביותר בין מעריכים.

מידע נוסף זמין במאמר נתונים קטגוריים: בעיות נפוצות בסדנה ללימוד מכונת למידה.

L

הפסד של ₁

#fundamentals

#Metric

פונקציית הפסד שמחשבת את הערך המוחלט של ההפרש בין ערכי התוויות בפועל לבין הערכים שהמודל חוזה. לדוגמה, הנה החישוב של הפסד L₁ עבור batch של חמש דוגמאות:

ערך בפועל של הדוגמה	הערך שהמודל חזה	הערך המוחלט של הדלתא
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		‫8 = הפסד L1

הפונקציה L₁ loss פחות רגישה לערכים חריגים מאשר הפונקציה L₂ loss.

השגיאה הממוצעת המוחלטת היא הפסד _L1 הממוצע לכל דוגמה.

לוחצים על הסמל כדי לראות את המתמטיקה הפורמלית.

$$ L_1 loss = \sum_{i=0}^n | y_i - \hat{y}_i |$$

כאשר:

• ‫$n$ הוא מספר הדוגמאות.
• ‫$y$ הוא הערך בפועל של התווית.
• ‫$\hat{y}$ הוא הערך שהמודל חוזה עבור $y$.

---

מידע נוסף זמין במאמר Linear regression: Loss (רגרסיה לינארית: הפסד) בסדרת המאמרים Machine Learning Crash Course (מבוא ללמידת מכונה).

הפסד L₂

#fundamentals

#Metric

פונקציית הפסד שמחשבת את ריבוע ההפרש בין ערכי התוויות בפועל לבין הערכים שהמודל חוזה. לדוגמה, הנה חישוב של הפסד L₂ עבור batch של חמש דוגמאות:

ערך בפועל של הדוגמה	הערך שהמודל חזה	ריבוע של דלתא
7	6	1
5	4	1
8	11	9
4	6	4
9	8	1
		‫16 = L2 loss

בגלל ההעלאה בריבוע, פונקציית ההפסד L₂ מגדילה את ההשפעה של ערכים חריגים. כלומר, הפסד L₂ מגיב בעוצמה רבה יותר לחיזויים לא טובים מאשר הפסד L₁. לדוגמה, ערך ההפסד L₁ עבור אצווה קודמת יהיה 8 ולא 16. שימו לב שחריג חשוד טעות יחיד מסביר 9 מתוך 16.

מודלים של רגרסיה משתמשים בדרך כלל בהפסד L₂ כפונקציית ההפסד.

השגיאה הריבועית הממוצעת היא הפסד _L2 הממוצע לכל דוגמה. שגיאה ריבועית היא שם נוסף לשגיאת L₂.

לוחצים על הסמל כדי לראות את המתמטיקה הפורמלית.

$$ L_2 loss = \sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$

כאשר:

• ‫$n$ הוא מספר הדוגמאות.
• ‫$y$ הוא הערך בפועל של התווית.
• ‫$\hat{y}$ הוא הערך שהמודל חוזה עבור $y$.

---

מידע נוסף זמין במאמר Logistic regression: Loss and regularization (רגרסיה לוגיסטית: הפסד ורגולריזציה) בסדנה בנושא למידת מכונה.

הערכות של מודלים גדולים של שפה (LLM)

#generativeAI

#Metric

קבוצה של מדדים ונקודות השוואה להערכת הביצועים של מודלים גדולים של שפה (LLM). ברמת העל, הערכות של מודלים גדולים של שפה (LLM):

• לעזור לחוקרים לזהות תחומים שבהם צריך לשפר את מודלי ה-LLM.
• הם שימושיים להשוואה בין מודלי שפה גדולים שונים ולזיהוי מודל השפה הגדול הטוב ביותר למשימה מסוימת.
• עוזרים להבטיח שהשימוש במודלים גדולים של שפה (LLM) יהיה בטוח ואתי.

מידע נוסף זמין במאמר מודלים גדולים של שפה (LLM) בקורס המקוצר על למידת מכונה.

הפסד

#fundamentals

#Metric

במהלך האימון של מודל בפיקוח, נמדד המרחק בין התחזית של המודל לבין התווית שלו.

פונקציית הפסד מחשבת את ההפסד.

מידע נוסף זמין במאמר רגרסיה ליניארית: הפסד בסדנה בנושא למידת מכונה.

פונקציית אובדן

#fundamentals

#Metric

במהלך האימון או הבדיקה, פונקציה מתמטית שמחשבת את ההפסד באצווה של דוגמאות. פונקציית הפסד מחזירה ערך הפסד נמוך יותר למודלים שמבצעים חיזויים טובים, מאשר למודלים שמבצעים חיזויים לא טובים.

המטרה של האימון היא בדרך כלל למזער את ההפסד שמוחזר על ידי פונקציית הפסד.

קיימים סוגים רבים ושונים של פונקציות אובדן. בוחרים את פונקציית ההפסד המתאימה לסוג המודל שאתם בונים. לדוגמה:

• הפונקציה אובדן _L2 (או השגיאה הריבועית הממוצעת) היא פונקציית האובדן של רגרסיה ליניארית.
• Log Loss היא פונקציית האובדן של רגרסיה לוגיסטית.

M

פירוק מטריצות

במתמטיקה, מנגנון למציאת המטריצות שמכפלתן הנקודתית קרובה למטריצת יעד.

במערכות המלצה, מטריצת היעד מכילה בדרך כלל את דירוגי המשתמשים של פריטים. לדוגמה, מטריצת היעד של מערכת להמלצות על סרטים יכולה להיראות כך, כאשר המספרים השלמים החיוביים הם דירוגי משתמשים ו-0 מציין שהמשתמש לא דירג את הסרט:

	קזבלנקה	סיפור פילדלפיה	הפנתר השחור	וונדר וומן	ספרות זולה
משתמש 1	5.0	3.0	0.0	2.0	0.0
משתמש 2	4.0	0.0	0.0	1.0	5.0
משתמש 3	3.0	1.0	4.0	5.0	0.0

מערכת ההמלצות לסרטים מנסה לחזות את דירוגי המשתמשים לסרטים שלא סווגו. לדוגמה, האם משתמש 1 יאהב את הסרט הפנתר השחור?

אחת הגישות למערכות המלצות היא שימוש בפירוק מטריצות כדי ליצור את שתי המטריצות הבאות:

• מטריצת משתמשים, בצורה של מספר המשתמשים כפול מספר המאפיינים של ההטמעה.
• מטריצת פריטים, בצורה של מספר הממדים של ההטמעה כפול מספר הפריטים.

לדוגמה, שימוש בפירוק מטריצה בשלושת המשתמשים ובחמישה הפריטים שלנו יכול להניב את מטריצת המשתמשים ומטריצת הפריטים הבאות:

User Matrix                 Item Matrix

1.1   2.3           0.9   0.2   1.4    2.0   1.2
0.6   2.0           1.7   1.2   1.2   -0.1   2.1
2.5   0.5

מכפלת מטריצת המשתמשים ומטריצת הפריטים היא מטריצת המלצות שמכילה לא רק את דירוגי המשתמשים המקוריים, אלא גם תחזיות לגבי הסרטים שכל משתמש לא צפה בהם. לדוגמה, נניח שהדירוג של משתמש 1 לסרט קזבלנקה הוא 5.0. הנקודה שמתאימה לתא הזה במטריצת ההמלצות צריכה להיות בסביבות 5.0, ואכן:

(1.1 * 0.9) + (2.3 * 1.7) = 4.9

והכי חשוב, האם משתמש 1 יאהב את הסרט Black Panther? מכפלה סקלרית של השורה הראשונה והעמודה השלישית תניב דירוג צפוי של 4.3:

(1.1 * 1.4) + (2.3 * 1.2) = 4.3

בדרך כלל, פירוק מטריצה יוצר מטריצת משתמשים ומטריצת פריטים, שביחד הן קומפקטיות משמעותית ממטריצת היעד.

MBPP

#Metric

קיצור של בעיות בסיסיות בעיקר ב-Python.

שגיאה ממוצעת מוחלטת (MAE)

#Metric

ההפסד הממוצע לכל דוגמה כשמשתמשים ב-L₁ loss. כדי לחשב את שגיאת הממוצע המוחלט, פועלים לפי השלבים הבאים:

1. חישוב הפסד L₁ עבור אצווה.
2. מחלקים את הפסד L₁ במספר הדוגמאות באצווה.

לוחצים על הסמל כדי לראות את המתמטיקה הפורמלית.

$$\text{Mean Absolute Error} = \frac{1}{n}\sum_{i=0}^n | y_i - \hat{y}_i |$$

where:‎

• ‫$n$ הוא מספר הדוגמאות.
• ‫$y$ הוא הערך בפועל של התווית.
• ‫$\hat{y}$ הוא הערך שהמודל חוזה עבור $y$.

---

לדוגמה, נניח שרוצים לחשב את הפסד L₁ בקבוצה הבאה של חמש דוגמאות:

ערך בפועל של הדוגמה	הערך שהמודל חזה	הפסד (ההפרש בין הערך בפועל לבין הערך החזוי)
7	6	1
5	4	1
8	11	3
4	6	2
9	8	1
		‫8 = הפסד L1

לכן, ערך הפסד L₁ הוא 8 ומספר הדוגמאות הוא 5. לכן, השגיאה הממוצעת המוחלטת היא:

Mean Absolute Error = L1 loss / Number of Examples
Mean Absolute Error = 8/5 = 1.6

השוואה בין שגיאה מוחלטת ממוצעת של ניגודיות לבין שגיאה ריבועית ממוצעת ושורש טעות ריבועית ממוצעת.

דיוק ממוצע ב-k (mAP@k)

#generativeAI

#Metric

הממוצע הסטטיסטי של כל הציונים של דיוק ממוצע ב-k במערך נתוני אימות. אחד השימושים בערך הממוצע של דיוק ממוצע ב-k הוא להעריך את איכות ההמלצות שנוצרות על ידי מערכת המלצות.

למרות שהביטוי 'ממוצע ממוצע' נשמע מיותר, השם של המדד מתאים. בסופו של דבר, המדד הזה מחשב את הממוצע של כמה ערכים של דיוק ממוצע ב-k.

כדי לראות דוגמה, לוחצים על הסמל.

נניח שאתם בונים מערכת המלצות שמפיקה רשימה מותאמת אישית של רומנים מומלצים לכל משתמש. על סמך המשוב ממשתמשים נבחרים, חישבתם את חמשת ציוני הדיוק הממוצעים הבאים ב-k (ציון אחד לכל משתמש):

• 0.73
• 0.77
• 0.67
• 0.82
• 0.76

לכן, הדיוק הממוצע ב-K הוא:

$$\text{mean } = \frac{\text{0.73 + 0.77 + 0.67 + 0.82 + 0.76}} {\text{5}} = \text{0.75}$$

---

שגיאה ריבועית ממוצעת (MSE)

#Metric

ההפסד הממוצע לכל דוגמה כשמשתמשים בהפסד _L. כך מחשבים את השגיאה הריבועית הממוצעת:

1. חישוב הפסד L₂ עבור אצווה.
2. מחלקים את הפסד L₂ במספר הדוגמאות באצווה.

לוחצים על הסמל כדי לראות את המתמטיקה הפורמלית.

$$\text{Mean Squared Error} = \frac{1}{n}\sum_{i=0}^n {(y_i - \hat{y}_i)}^2$$ כאשר:

• ‫$n$ הוא מספר הדוגמאות.
• ‫$y$ הוא הערך בפועל של התווית.
• ‫$\hat{y}$ הוא החיזוי של המודל עבור $y$.

---

לדוגמה, נניח שאתם רוצים לחשב את הפסד על קבוצה של חמש דוגמאות:

ערך בפועל	החיזוי של המודל	הפסד	פונקציית הפסד ריבועי
7	6	1	1
5	4	1	1
8	11	3	9
4	6	2	4
9	8	1	1
			‫16 = L2 loss

לכן, השגיאה הריבועית הממוצעת היא:

Mean Squared Error = L2 loss / Number of Examples
Mean Squared Error = 16/5 = 3.2

השגיאה הריבועית הממוצעת היא אופטימיזציה פופולרית לאימון, במיוחד עבור רגרסיה לינארית.

השוואה בין שורש טעות ריבועית ממוצעת לבין טעות מוחלטת ממוצעת ושגיאה ריבועית ממוצעת.

‫TensorFlow Playground משתמש בטעות ריבועית ממוצעת כדי לחשב את ערכי ההפסד.

כדי לראות פרטים נוספים על חריגים, לוחצים על הסמל.

ערכים חריגים משפיעים מאוד על שגיאה ריבועית ממוצעת. לדוגמה, הפסד של 1 הוא הפסד בריבוע של 1, אבל הפסד של 3 הוא הפסד בריבוע של 9. בדוגמה עם אובדן של 3 חשבונות בטבלה שלמעלה, האובדן הזה מייצג כ-56% משגיאת הריבוע הממוצעת, בעוד שכל אחת מהדוגמאות עם אובדן של חשבון אחד מייצגת רק 6% משגיאת הריבוע הממוצעת.

לערכים חריגים אין השפעה חזקה על שגיאה ממוצעת מוחלטת כמו על שגיאה ממוצעת ריבועית. לדוגמה, איבוד של 3 חשבונות מייצג רק כ-38% מהשגיאה הממוצעת המוחלטת.

חיתוך הוא כיוון אחד למנוע ממקרים חריגים קיצוניים לפגוע ביכולת החיזוי של המודל.

---

ערך

#TensorFlow

#Metric

נתון סטטיסטי שחשוב לכם.

יעד הוא מדד שמערכת למידת מכונה מנסה לבצע לו אופטימיזציה.

Metrics API (tf.metrics)

#Metric

‫TensorFlow API להערכת מודלים. לדוגמה, tf.metrics.accuracy קובע את התדירות שבה התחזיות של מודל תואמות לתוויות.

הפסד מינימקס

#Metric

פונקציית הפסד של רשתות יריבות גנרטיביות, שמבוססת על אנטרופיה צולבת בין ההתפלגות של הנתונים שנוצרו לבין הנתונים האמיתיים.

הפסד מינימקס משמש במאמר הראשון לתיאור רשתות יריבות גנרטיביות.

מידע נוסף זמין במאמר פונקציות הפסד בקורס בנושא רשתות יריבות גנרטיביות.

קיבולת המודל

#Metric

מורכבות הבעיות שהמודל יכול ללמוד. ככל שהבעיות שמודל יכול ללמוד מורכבות יותר, כך הקיבולת של המודל גבוהה יותר. הקיבולת של מודל בדרך כלל גדלה עם מספר הפרמטרים של המודל. הגדרה רשמית של הקיבולת של מודל סיווג מופיעה במאמר בנושא ממד VC.

מומנטום

אלגוריתם מורכב של ירידת גרדיאנט שבו שלב הלמידה תלוי לא רק בנגזרת בשלב הנוכחי, אלא גם בנגזרות של השלבים שקדמו לו. המומנטום כולל חישוב של ממוצע נע משוקלל אקספוננציאלית של הגרדיאנטים לאורך זמן, בדומה למומנטום בפיזיקה. המומנטום מונע לפעמים את התקיעה של מצב למידה במינימום מקומי.

בעיות בסיסיות ב-Python (MBPP)

#Metric

מערך נתונים להערכת רמת המיומנות של מודל שפה גדולה (LLM) ביצירת קוד Python. ‫Mostly Basic Python Problems כולל כ-1,000 בעיות תכנות שמקורן במיקור המונים. כל בעיה במערך הנתונים מכילה:

• תיאור המשימה
• קוד הפתרון
• שלושה מקרי בדיקה אוטומטיים

לא

סיווג שלילי

#fundamentals

#Metric

בסיווג בינארי, מחלקים את הנתונים לשתי קבוצות: חיובית ושלילית. הסיווג החיובי הוא הדבר או האירוע שהמודל בודק, והסיווג השלילי הוא האפשרות השנייה. לדוגמה:

• הסיווג השלילי בבדיקה רפואית יכול להיות 'לא גידול'.
• הסיווג השלילי במודל סיווג של אימייל יכול להיות 'לא ספאם'.

ההגדרה הזו שונה מהכיתה החיובית.

O

יעד

#Metric

מדד שהאלגוריתם מנסה לבצע לו אופטימיזציה.

פונקציית היעד

#Metric

הנוסחה המתמטית או המדד שהמודל מנסה לבצע אופטימיזציה לגביהם. לדוגמה, פונקציית היעד של רגרסיה לינארית היא בדרך כלל Mean Squared Loss (אובדן ממוצע בריבוע). לכן, כשמאמנים מודל רגרסיה לינארית, האימון נועד לצמצם את אובדן המידע הממוצע בריבוע.

במקרים מסוימים, המטרה היא למקסם את פונקציית היעד. לדוגמה, אם פונקציית היעד היא דיוק, המטרה היא למקסם את הדיוק.

מידע נוסף זמין במאמר בנושא הפסד.

P

pass at k (pass@k)

#Metric

מדד לקביעת איכות הקוד (לדוגמה, Python) שנוצר על ידי מודל שפה גדול. באופן ספציפי יותר, הערך של pass at k מציין את הסבירות שלפחות בלוק אחד מתוך k בלוקים של קוד שנוצרו יעבור את כל בדיקות היחידה שלו.

למודלים גדולים של שפה (LLM) יש לעיתים קרובות קושי ליצור קוד טוב לבעיות תכנות מורכבות. מהנדסי תוכנה מתמודדים עם הבעיה הזו על ידי הנחיית מודל השפה הגדול (LLM) ליצור כמה (k) פתרונות לאותה בעיה. לאחר מכן, מהנדסי תוכנה בודקים כל אחד מהפתרונות באמצעות בדיקות יחידה. החישוב של pass@k תלוי בתוצאה של בדיקות היחידה:

• אם אחד או יותר מהפתרונות האלה עוברים את בדיקת היחידה, אז ה-LLM עובר את האתגר של יצירת הקוד.
• אם אף אחד מהפתרונות לא עובר את בדיקת היחידה, מודל ה-LLM נכשל באתגר הזה של יצירת קוד.

הנוסחה לחישוב המעבר ב-k היא:

\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]

באופן כללי, ערכים גבוהים יותר של k מניבים ציונים גבוהים יותר של מעבר ב-k, אבל ערכים גבוהים יותר של k דורשים יותר משאבים של מודל שפה גדול (LLM) ובדיקות יחידה.

לוחצים על הסמל כדי לראות דוגמה.

נניח שמהנדס תוכנה מבקש ממודל שפה גדול ליצור k=10 פתרונות ל-n=50 בעיות מאתגרות בתכנות. אלה התוצאות:

• 30 כרטיסים
• 20 נכשלו

לכן, הציון שמעיד על מעבר הוא 10:

$$\text{pass at 10} = \frac{\text{30}} {\text{50}} = 0.6$$

---

ביצועים

#Metric

מונח עם עומס יתר שכולל את המשמעויות הבאות:

• המשמעות הסטנדרטית בהנדסת תוכנה. כלומר: עד כמה התוכנה הזו פועלת מהר (או ביעילות)?
• המשמעות בהקשר של למידת מכונה. התשובה לשאלה הבאה: עד כמה המודל הזה מדויק? כלומר, עד כמה התחזיות של המודל טובות?

חשיבות משתנים בתמורה

#df

#Metric

סוג של חשיבות משתנה שמעריך את העלייה בשגיאת החיזוי של מודל אחרי שינוי הערכים של התכונה. חשיבות המשתנה בפרמוטציה היא מדד שלא תלוי במודל.

תמיהה

#Metric

מדד אחד שמשקף את מידת ההצלחה של מודל בהשגת המטרה שלו. לדוגמה, נניח שהמשימה שלכם היא לקרוא את כמה האותיות הראשונות של מילה שמשתמש מקליד במקלדת של טלפון, ולהציע רשימה של מילים אפשריות להשלמה. הערך של Perplexity, ‏ P, למשימה הזו הוא בערך מספר הניחושים שצריך להציע כדי שהרשימה תכיל את המילה שהמשתמש מנסה להקליד.

המדד Perplexity קשור לcross-entropy באופן הבא:

$$P= 2^{-\text{cross entropy}}$$

positive class

#fundamentals

#Metric

הכיתה שאתם נבחנים בה.

לדוגמה, המחלקה החיובית במודל לסרטן יכולה להיות 'גידול'. הסיווג החיובי במודל סיווג של אימייל יכול להיות 'ספאם'.

הניגוד לסיווג שלילי.

כדי לראות טיפים ממשתמשים נוספים, לוחצים על הסמל.

המונח סיווג חיובי עלול לבלבל, כי התוצאה ה'חיובית' של הרבה בדיקות היא לרוב תוצאה לא רצויה. לדוגמה, המחלקה החיובית בהרבה בדיקות רפואיות מתאימה לגידולים או למחלות. באופן כללי, אתם רוצים לשמוע מרופא את המילים: "מזל טוב! תוצאות הבדיקה שלך היו שליליות". בכל מקרה, המחלקה החיובית היא האירוע שהבדיקה מנסה למצוא.

אמנם, אתם בודקים בו-זמנית את המחלקות החיוביות והשליליות.

---

PR AUC (השטח מתחת לעקומת ה-PR)

#Metric

השטח מתחת לעקומת הדיוק וההחזרה שחושבה על ידי אינטרפולציה, שהתקבלה משרטוט נקודות (החזרה, דיוק) עבור ערכים שונים של סף הסיווג.

דיוק

#fundamentals

#Metric

מדד למודלים של סיווג שעונה על השאלה הבאה:

כשהמודל חזה את הסיווג החיובי, מה אחוז החיזויים הנכונים?

זו הנוסחה:

$$\text{Precision} = \frac{\text{true positives}} {\text{true positives} + \text{false positives}}$$

where:‎

• חיובי אמיתי פירושו שהמודל חזה נכון את המחלקה החיובית.
• תוצאה חיובית שגויה פירושה שהמודל טעה וחיזוי את הסיווג החיובי.

לדוגמה, נניח שמודל מסוים הפיק 200 חיזויים חיוביים. מתוך 200 התחזיות החיוביות האלה:

• 150 היו TRUE.
• 50 מהן היו תוצאות חיוביות כוזבות.

במקרה זה:

$$\text{Precision} = \frac{\text{150}} {\text{150} + \text{50}} = 0.75$$

ההגדרה הזו שונה מדיוק ומהחזרה.

מידע נוסף זמין במאמר סיווג: דיוק, היזכרות, פרסיזיה ומדדים קשורים בסדנה ללמידת מכונה.

דיוק ב-k‏ (precision@k)

#Metric

מדד להערכת רשימה מדורגת (מסודרת) של פריטים. המדד 'דיוק ב-k' מזהה את החלק של k הפריטים הראשונים ברשימה שהם 'רלוונטיים'. כלומר:

\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]

הערך של k צריך להיות קטן מאורך הרשימה שמוחזרת או שווה לו. שימו לב שאורך הרשימה שמוחזרת לא נכלל בחישוב.

רלוונטיות היא לרוב סובייקטיבית. אפילו מעריכים אנושיים מומחים חלוקים בדעתם לגבי הפריטים הרלוונטיים.

השווה ל:

• דיוק ממוצע ב-k
• דיוק ממוצע ב-k

כדי לראות דוגמה, לוחצים על הסמל.

נניח שמודל שפה גדול מקבל את השאילתה הבאה:

List the 6 funniest movies of all time in order.

מודל השפה הגדול מחזיר את הרשימה שמוצגת בשתי העמודות הראשונות של הטבלה הבאה:

מיקום	סרט	רלוונטי?
1	The General	כן
2	Mean Girls	כן
3	Platoon	לא
4	שושבינות	כן
5	האזרח קיין	לא
6	This is Spinal Tap	כן

שניים מתוך שלושת הסרטים הראשונים רלוונטיים, ולכן רמת הדיוק ב-3 היא:

$$\text{precision at 3} = \frac{\text{2}} {\text{3}} = 0.67$$

שלושה מתוך חמשת הסרטים הראשונים מצחיקים מאוד, ולכן הדיוק ב-5 הוא:

$$\text{precision at 5} = \frac{\text{3}} {\text{5}} = 0.6$$

---

עקומת דיוק-החזרה

#Metric

עקומת הדיוק לעומת ההחזרה בספי סיווג שונים.

הטיה בתחזית

#Metric

ערך שמציין את המרחק בין הממוצע של התחזיות לבין הממוצע של התוויות במערך הנתונים.

לא להתבלבל עם מונח ההטיה במודלים של למידת מכונה או עם הטיה באתיקה ובהוגנות.

שוויון חיזוי

#responsible

#Metric

מדד הוגנות שבודק אם שיעורי הדיוק שווים עבור קבוצות משנה שנבדקות במודל סיווג נתון.

לדוגמה, מודל שמנבא קבלה למכללה יעמוד בדרישות של שוויון חיזוי לפי לאום אם שיעור הדיוק שלו זהה עבור אנשים מליליפוט ואנשים מברובדינגנאג.

לפעמים קוראים לשיטה הזו גם שוויון חזוי בשיעורי ההמרה.

דיון מפורט יותר בנושא שוויון חיזוי זמין במאמר הסבר על הגדרות ההוגנות (סעיף 3.2.1).

השוואת מחירים חזויה

#responsible

#Metric

שם נוסף לשוויון חיזוי.

פונקציית צפיפות ההסתברות

#Metric

פונקציה שמזהה את התדירות של דגימות נתונים עם ערך מסוים בדיוק. כשערכים של מערך נתונים הם מספרים רציפים עם נקודה צפה, התאמות מדויקות הן נדירות. עם זאת, שילוב של פונקציית צפיפות הסתברות מהערך x לערך y מניב את התדירות הצפויה של דגימות נתונים בין x ל-y.

לדוגמה, נניח שיש התפלגות נורמלית עם ממוצע של 200 וסטיית תקן של 30. כדי לקבוע את התדירות הצפויה של דגימות נתונים שנמצאות בטווח 211.4 עד 218.7, אפשר לבצע אינטגרציה של פונקציית צפיפות ההסתברות להתפלגות נורמלית מ-211.4 עד 218.7.

R

הבנת הנקרא עם מערך נתונים של חשיבה הגיונית (ReCoRD)

#Metric

מערך נתונים להערכת היכולת של מודל LLM לבצע חשיבה רציונלית. כל דוגמה במערך הנתונים מכילה שלושה רכיבים:

• פסקה או שתיים מכתבה
• שאילתה שבה אחת מהישויות שזוהו במפורש או במרומז בפסקה מוסתרת.
• התשובה (שם הישות שצריך להופיע במסכה)

רשימה מקיפה של דוגמאות מופיעה במאמר בנושא ReCoRD.

‫ReCoRD הוא רכיב של SuperGLUE ensemble.

RealToxicityPrompts

#Metric

מערך נתונים שמכיל קבוצה של התחלות משפטים שעשויות להכיל תוכן רעיל. משתמשים במערך הנתונים הזה כדי להעריך את היכולת של מודל שפה גדול (LLM) ליצור טקסט לא רעיל כדי להשלים את המשפט. בדרך כלל, משתמשים ב-Perspective API כדי לקבוע את רמת הביצוע של ה-LLM במשימה הזו.

פרטים נוספים זמינים במאמר RealToxicityPrompts: Evaluating Neural Toxic Degeneration in Language Models.

recall

#fundamentals

#Metric

מדד למודלים של סיווג שעונה על השאלה הבאה:

כאשר אמת קרקע הייתה הסיווג החיובי, איזה אחוז מהתחזיות המודל זיהה נכון כסיווג החיובי?

זו הנוסחה:

\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]

where:‎

• חיובי אמיתי פירושו שהמודל חזה נכון את המחלקה החיובית.
• שלילי שגוי פירושו שהמודל טעה וחיזה את הסיווג השלילי.

לדוגמה, נניח שהמודל שלכם ביצע 200 חיזויים על דוגמאות שבהן אמת הקרקע הייתה הסיווג החיובי. מתוך 200 התחזיות האלה:

• 180 היו TRUE חיוביים.
• 20 מהן היו תוצאות שליליות שגויות.

במקרה זה:

\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]

לוחצים על הסמל כדי לראות טיפים ממשתמשים לגבי מערכי נתונים עם חוסר איזון בין הכיתות.

המדד Recall שימושי במיוחד לקביעת כוח החיזוי של מודלים לסיווג שבהם המחלקה החיובית נדירה. לדוגמה, נניח שיש מערך נתונים עם חוסר איזון בין המחלקות שבו המחלקה החיובית למחלה מסוימת מופיעה רק אצל 10 מתוך מיליון מטופלים. נניח שהמודל שלכם מבצע חמישה מיליון חיזויים שמניבים את התוצאות הבאות:

• 30 TRUE חיוביים
• 20 FALSE Negatives
• 4,999,000 תוצאות שליליות TRUE
• 950 FALSE Positives

לכן, ערך ה-recall של המודל הזה הוא:

recall = TP / (TP + FN)
recall = 30 / (30 + 20) = 0.6 = 60%

לעומת זאת, רמת הדיוק של המודל הזה היא:

accuracy = (TP + TN) / (TP + TN + FP + FN)
accuracy = (30 + 4,999,000) / (30 + 4,999,000 + 950 + 20) = 99.98%

ערך הדיוק הגבוה הזה נראה מרשים, אבל הוא חסר משמעות. המדד Recall שימושי הרבה יותר למערכי נתונים לא מאוזנים מבחינת כמות הנתונים בכל מחלקה מאשר המדד Accuracy.

---

מידע נוסף זמין במאמר סיווג: דיוק, היזכרות, פרסיזיה ומדדים קשורים.

ריקול ב-k (recall@k)

#Metric

מדד להערכת מערכות שמפיקות רשימה מדורגת (מסודרת) של פריטים. המדד Recall at k מזהה את החלק של הפריטים הרלוונטיים מתוך k הפריטים הראשונים ברשימה, מתוך המספר הכולל של הפריטים הרלוונטיים שהוחזרו.

\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]

השוואה לדיוק ב-k.

כדי לראות דוגמה, לוחצים על הסמל.

נניח שמודל שפה גדול מקבל את השאילתה הבאה:

List the 10 funniest movies of all time in order.

מודל השפה הגדול מחזיר את הרשימה שמוצגת בשתי העמודות הראשונות:

מיקום	סרט	רלוונטי?
1	The General	כן
2	Mean Girls	כן
3	Platoon	לא
4	שושבינות	כן
5	This is Spinal Tap	כן
6	Airplane!	כן
7	יום המרמיטה	כן
8	מונטי פייתון והגביע הקדוש	כן
9	אופנהיימר	לא
10	Clueless	כן

שמונה מהסרטים ברשימה הקודמת הם מאוד מצחיקים, ולכן הם נחשבים ל'פריטים רלוונטיים ברשימה'. לכן, 8 יהיה המכנה בכל החישובים של ההחזרה ב-k. מה לגבי המונה? ובכן, 3 מתוך 4 הפריטים הראשונים רלוונטיים, ולכן ערך הזיכרון ב-4 הוא:

$$\text{recall at 4} = \frac{\text{3}} {\text{8}} = 0.375$$

7 מתוך 8 הסרטים הראשונים מצחיקים מאוד, ולכן רמת הזכירה בסרטון 8 היא:

$$\text{recall at 8} = \frac{\text{7}} {\text{8}} = 0.875$$

---

זיהוי של הסקה לוגית מטקסט (RTE)

#Metric

מערך נתונים להערכת היכולת של מודל שפה גדול לקבוע אם אפשר להסיק השערה (לוגית) מקטע טקסט. כל דוגמה בהערכה של RTE מורכבת משלושה חלקים:

• קטע, בדרך כלל מכתבות חדשותיות או ממאמרי ויקיפדיה
• השערה
• התשובה הנכונה, שהיא אחת מהאפשרויות הבאות:
  • True, meaning the hypothesis can be entailed from the passage
  • False, כלומר ההשערה לא נגזרת מהפסקה

לדוגמה:

• פסקה: האירו הוא המטבע של האיחוד האירופי.
• השערה: בצרפת משתמשים באירו כמטבע.
• היסק: True, כי צרפת היא חלק מהאיחוד האירופי.

RTE הוא רכיב של SuperGLUE.

ReCoRD

#Metric

קיצור של Reading Comprehension with Commonsense Reasoning Dataset (הבנת הנקרא עם מערך נתונים של חשיבה הגיונית).

עקומת ROC (מאפיין הפעולה של המקלט)

#fundamentals

#Metric

תרשים של שיעור החיוביים האמיתיים לעומת שיעור החיוביים הכוזבים עבור ערכי סף שונים לסיווג בסיווג בינארי.

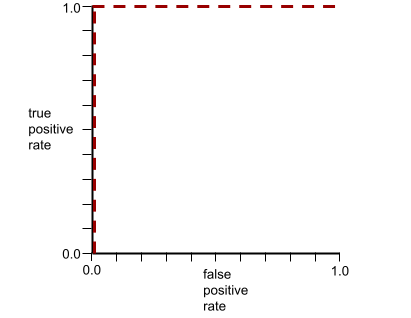
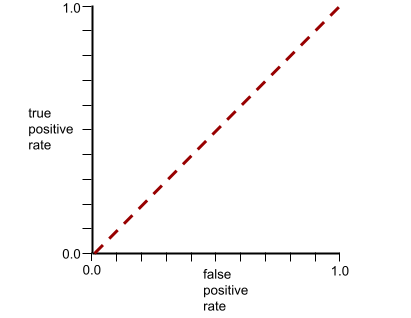
הצורה הסגורה של עקומת ROC מצביעה על היכולת של מודל סיווג בינארי להפריד בין סיווגים חיוביים לסיווגים שליליים. נניח, לדוגמה, שמודל סיווג בינארי מפריד בצורה מושלמת בין כל המחלקות השליליות לבין כל המחלקות החיוביות:

עקומת ה-ROC של המודל הקודם נראית כך:

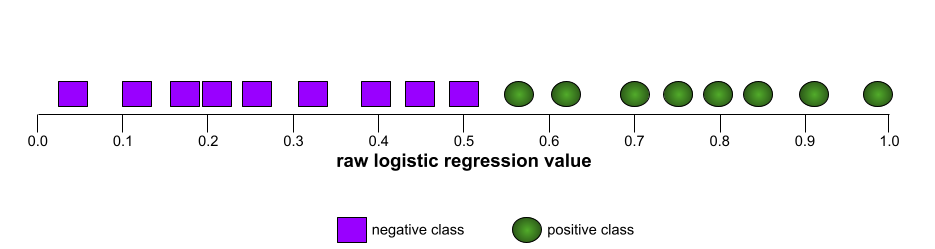
לעומת זאת, באיור הבא מוצגים ערכי הרגרסיה הלוגיסטית הגולמיים של מודל גרוע שלא מצליח להפריד בין מחלקות שליליות למחלקות חיוביות:

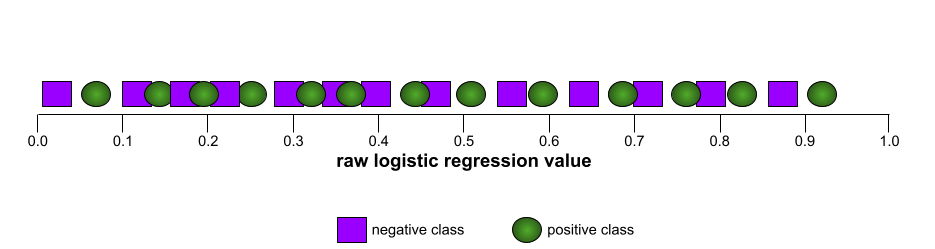
עקומת ה-ROC של המודל הזה נראית כך:

בינתיים, בעולם האמיתי, רוב מודלי הסיווג הבינארי מפרידים בין מחלקות חיוביות ושליליות במידה מסוימת, אבל בדרך כלל לא בצורה מושלמת. לכן, עקומת ROC אופיינית נמצאת איפשהו בין שני הקצוות:

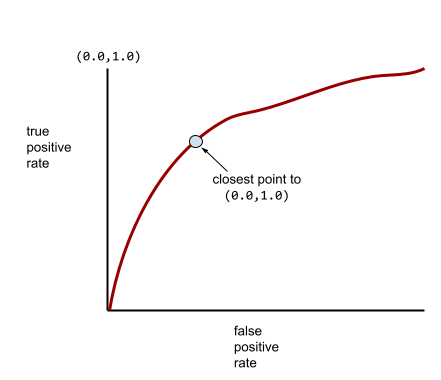
הנקודה בעקומת ROC שהכי קרובה ל-(0.0,1.0) מזהה באופן תיאורטי את סף הסיווג האידיאלי. עם זאת, יש כמה בעיות אחרות בעולם האמיתי שמשפיעות על הבחירה של סף הסיווג האידיאלי. לדוגמה, אולי FALSE שליליים גורמים להרבה יותר כאב מאשר FALSE חיוביים.

מדד מספרי שנקרא AUC מסכם את עקומת ה-ROC לערך יחיד של נקודה צפה.

שורש טעות ריבועית ממוצעת (RMSE)

#fundamentals

#Metric

השורש הריבועי של הטעות הריבועית הממוצעת.

ROUGE (Recall-Oriented Understudy for Gisting Evaluation)

#Metric

משפחה של מדדים להערכת מודלים של סיכום אוטומטי ותרגום מכונה. מדדי ROUGE קובעים את מידת החפיפה בין טקסט ייחוס לבין טקסט שנוצר על ידי מודל ML. כל אחד מהמדדים במשפחת ROUGE מודד חפיפה בצורה שונה. ציוני ROUGE גבוהים יותר מצביעים על דמיון רב יותר בין טקסט ההפניה לבין הטקסט שנוצר, בהשוואה לציוני ROUGE נמוכים יותר.

בדרך כלל, כל חבר במשפחת ROUGE יוצר את המדדים הבאים:

• דיוק
• זכירות
• F₁

הערה: המדדים דיוק והיזכרות ב-ROUGE שונים במידה מסוימת מהמדדים המסורתיים של דיוק והיזכרות.

לפרטים נוספים ולעיון בדוגמאות, ראו:

• ROUGE-L
• ROUGE-N
• ROUGE-S

הערה: BLEU ו-BLEURT עוברים אופטימיזציה לדיוק, ואילו ROUGE עובר אופטימיזציה לשליפה. לכן, BLEU ו-BLEURT הם מדדים טובים יותר להערכת תרגום אוטומטי (כי הדגש הוא על דיוק), ואילו ROUGE הוא מדד טוב יותר לסיכום (כי הדגש הוא על היזכרות).

ROUGE-L

#Metric

חבר במשפחת ROUGE שמתמקד באורך של הרצף המשותף הארוך ביותר בטקסט ההפניה ובטקסט שנוצר. הנוסחאות הבאות משמשות לחישוב ההחזרה והדיוק של ROUGE-L:

$$\text{ROUGE-L recall} = \frac{\text{longest common sequence}} {\text{number of words in the reference text} }$$

$$\text{ROUGE-L precision} = \frac{\text{longest common sequence}} {\text{number of words in the generated text} }$$

אחר כך אפשר להשתמש ב-F₁ כדי לסכם את הנתונים של ROUGE-L recall ו-ROUGE-L precision למדד אחד:

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{ROUGE-L recall} * \text{ROUGE-L precision}} {\text{ROUGE-L recall} + \text{ROUGE-L precision} }$$

לוחצים על הסמל כדי לראות דוגמה לחישוב של ROUGE-L.

כדאי לעיין בטקסט המקורי ובטקסט שנוצר.

קטגוריה	מי הפיק?	טקסט
טקסט לדוגמה	מתרגם אנושי	אני רוצה להבין מגוון רחב של דברים.
הטקסט שנוצר	מודל ML	אני רוצה ללמוד הרבה דברים.

לכן:

• הרצף המשותף הארוך ביותר הוא 5 (I want to of things)
• מספר המילים בטקסט ההפניה הוא 9.
• מספר המילים בטקסט שנוצר הוא 7.

כתוצאה מכך:

$$\text{ROUGE-L recall} = \frac{\text{5}} {\text{9} } = 0.56$$

$$\text{ROUGE-L precision} = \frac{\text{5}} {\text{7} } = 0.71$$

$$\text{ROUGE-L F} {_1} = \frac{\text{2} * \text{0.56} * \text{0.71}} {\text{0.56} + \text{0.71} } = 0.63$$

---

המדד ROUGE-L מתעלם ממעברי שורה בטקסט הייחוס ובטקסט שנוצר, ולכן הרצף המשותף הארוך ביותר יכול לחצות כמה משפטים. אם טקסט ההפניה והטקסט שנוצר כוללים כמה משפטים, מדד טוב יותר הוא בדרך כלל וריאציה של ROUGE-L שנקראת ROUGE-Lsum. המדד ROUGE-Lsum קובע את הרצף המשותף הארוך ביותר לכל משפט בפסקה, ואז מחשב את הממוצע של הרצפים המשותפים הארוכים האלה.

לוחצים על הסמל כדי לראות דוגמה לחישוב של ROUGE-Lsum.

כדאי לעיין בטקסט המקורי ובטקסט שנוצר.

קטגוריה	מי הפיק?	טקסט
טקסט לדוגמה	מתרגם אנושי	הפלטפורמה של Google Mars יבשה. כמעט כל המים נמצאים עמוק מתחת לאדמה.
הטקסט שנוצר	מודל ML	ל-Google Mars יש פלטפורמה יבשה. עם זאת, רוב המים נמצאים מתחת לאדמה.

לכן:

	המשפט הראשון	המשפט השני
הרצף המשותף הארוך ביותר	‫2 (Mars dry)	‫3 (מים מתחת לפני הקרקע)
אורך המשפט של טקסט העזר	6	7
אורך המשפט בטקסט שנוצר	5	8

לכן:

$$\text{recall of first sentence} = \frac{\text{2}} {\text{6}} = 0.33 $$

$$\text{recall of second sentence} = \frac{\text{3}} {\text{7}} = 0.43 $$

$$\text{ROUGE-Lsum recall} = \frac{\text{0.33} + \text{0.43}} {\text{2}} = 0.38 $$

$$\text{precision of first sentence} = \frac{\text{2}} {\text{5}} = 0.4 $$

$$\text{precision of second sentence} = \frac{\text{3}} {\text{8}} = 0.38 $$

$$\text{ROUGE-Lsum precision} = \frac{\text{0.4} + \text{0.38}} {\text{2}} = 0.39 $$

$$\text{ROUGE-Lsum F}{_1} = \frac{\text{2} * \text{0.38} * \text{0.39}} {\text{0.38} + \text{0.39}} = 0.38 $$

---

ROUGE-N

#Metric

קבוצה של מדדים במשפחת ROUGE שמשווה בין ה-N-grams המשותפים בגודל מסוים בטקסט ההשוואה לבין הטקסט שנוצר. לדוגמה:

• המדד ROUGE-1 מודד את מספר הטוקנים המשותפים בטקסט ההפניה ובטקסט שנוצר.
• ‫ROUGE-2 מודד את מספר הביגרמות (2-גרמות) המשותפות בטקסט ההפניה ובטקסט שנוצר.
• המדד ROUGE-3 מודד את מספר הטריגרמים (3-גרמים) המשותפים בטקסט ההפניה ובטקסט שנוצר.

אפשר להשתמש בנוסחאות הבאות כדי לחשב את מדד הזיכרון (recall) של ROUGE-N ואת מדד הדיוק (precision) של ROUGE-N לכל חבר במשפחת ROUGE-N:

$$\text{ROUGE-N recall} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the reference text} }$$

$$\text{ROUGE-N precision} = \frac{\text{number of matching N-grams}} {\text{number of N-grams in the generated text} }$$

אחר כך אפשר להשתמש ב-F₁ כדי לצמצם את הנתונים של ROUGE-N recall ו-ROUGE-N precision למדד אחד:

$$\text{ROUGE-N F}{_1} = \frac{\text{2} * \text{ROUGE-N recall} * \text{ROUGE-N precision}} {\text{ROUGE-N recall} + \text{ROUGE-N precision} }$$

לוחצים על הסמל כדי לראות דוגמה.

נניח שאתם מחליטים להשתמש ב-ROUGE-2 כדי למדוד את היעילות של תרגום שבוצע על ידי מודל ML בהשוואה לתרגום שבוצע על ידי מתרגם אנושי.

קטגוריה	מי הפיק?	טקסט	ביגרמות
טקסט לדוגמה	מתרגם אנושי	אני רוצה להבין מגוון רחב של דברים.	אני רוצה, רוצה, להבין, להבין מגוון, מגוון רחב, רחב של דברים
הטקסט שנוצר	מודל ML	אני רוצה ללמוד הרבה דברים.	I want, want to, to learn, learn plenty, plenty of, of things

לכן:

• מספר ה-2-גרמים התואמים הוא 3 (I want,‏ want to ו-of things).
• מספר ה-2-גרמים בטקסט ההפניה הוא 8.
• מספר ה-2-גרמים בטקסט שנוצר הוא 6.

כתוצאה מכך:

$$\text{ROUGE-2 recall} = \frac{\text{3}} {\text{8} } = 0.375$$

$$\text{ROUGE-2 precision} = \frac{\text{3}} {\text{6} } = 0.5$$

$$\text{ROUGE-2 F}{_1} = \frac{\text{2} * \text{0.375} * \text{0.5}} {\text{0.375} + \text{0.5} } = 0.43$$

---

ROUGE-S

#Metric

גרסה סלחנית של ROUGE-N שמאפשרת התאמה של skip-gram. כלומר, ROUGE-N סופר רק N-grams שתואמים בדיוק, אבל ROUGE-S סופר גם N-grams שמפרידה ביניהם מילה אחת או יותר. לדוגמה, שקול את הדברים הבאים:

• טקסט להפניה: White clouds
• טקסט שנוצר: White billowing clouds

כשמחשבים את ROUGE-N, ה-2-gram, ‏ White clouds לא תואם ל-White billowing clouds. עם זאת, כשמחשבים את ROUGE-S, ‏ White clouds תואם ל-White billowing clouds.

R בריבוע

#Metric

מדד רגרסיה שמציין כמה מהשונות בתווית נובעת מתכונה ספציפית או מקבוצת תכונות. מקדם המתאם R² הוא ערך בין 0 ל-1, שאפשר לפרש אותו באופן הבא:

• ערך של 0 ב-R-squared מציין שאף אחת מהוריאציות של תווית לא נובעת ממערכת התכונות.
• ערך של 1 ב-R בריבוע מציין שכל הוריאציה של התווית נובעת מקבוצת התכונות.
• ערך R בריבוע בין 0 ל-1 מציין את המידה שבה אפשר לחזות את הוריאציה של התווית ממאפיין מסוים או מקבוצת המאפיינים. לדוגמה, אם ערך ה-R בריבוע הוא 0.10, המשמעות היא ש-10 אחוז מהשונות בתווית נובעים מקבוצת התכונות. אם ערך ה-R בריבוע הוא 0.20, המשמעות היא ש-20 אחוז מהשונות נובעים מקבוצת התכונות, וכן הלאה.

R בריבוע הוא הריבוע של מקדם המתאם של פירסון בין הערכים שהמודל חזה לבין אמת הקרקע.

RTE

#Metric

קיצור של Recognizing Textual Entailment.

S

דירוג

#Metric

החלק במערכת ההמלצות שמספק ערך או דירוג לכל פריט שנוצר בשלב יצירת המועמדים.

מדד הדמיון

#clustering

#Metric

באלגוריתמים של אשכולות, המדד שמשמש לקביעת מידת הדמיון בין שתי דוגמאות.

sparsity

#Metric

מספר הרכיבים שמוגדרים לאפס (או לערך null) בווקטור או במטריצה, חלקי המספר הכולל של הערכים בווקטור או במטריצה. לדוגמה, נניח שיש מטריצה עם 100 רכיבים, שבה 98 תאים מכילים אפס. החישוב של sparsity מתבצע כך:

$$ {\text{sparsity}} = \frac{\text{98}} {\text{100}} = {\text{0.98}} $$

דלילות מאפיינים מתייחסת לדלילות של וקטור מאפיינים, ודלילות מודל מתייחסת לדלילות של משקלי המודל.

SQuAD

#Metric

ראשי תיבות של Stanford Question Answering Dataset (מערך נתונים של סטנפורד למענה על שאלות), שהוצג במאמר SQuAD: 100,000+ Questions for Machine Comprehension of Text (מערך SQuAD: יותר מ-100,000 שאלות להבנת טקסט על ידי מכונה). השאלות במערך הנתונים הזה מגיעות מאנשים ששואלים שאלות על מאמרים בוויקיפדיה. לחלק מהשאלות ב-SQuAD יש תשובות, אבל לחלק אחר אין תשובות בכוונה. לכן, אפשר להשתמש ב-SQuAD כדי להעריך את היכולת של מודל שפה גדול (LLM) לבצע את שתי הפעולות הבאות:

• לענות על שאלות שאפשר לענות עליהן.
• לזהות שאלות שאי אפשר לענות עליהן.

התאמה מדויקת בשילוב עם F₁ הם המדדים הנפוצים ביותר להערכת מודלים גדולים של שפה (LLM) בהשוואה ל-SQuAD.

squared hinge loss

#Metric

הריבוע של הפסד הציר. הפסד ציר בריבוע מעניש חריגים בצורה חמורה יותר מאשר הפסד ציר רגיל.

squared loss

#fundamentals

#Metric

מילה נרדפת לירידה ברמת _L2.

SuperGLUE

#Metric

קבוצה של מערכי נתונים לדירוג היכולת הכוללת של מודל שפה גדול (LLM) להבין וליצור טקסט. האנסמבל מורכב ממערכי הנתונים הבאים:

• שאלות בוליאניות (BoolQ)
• CommitmentBank (CB)
• בחירת חלופות סבירות (COPA)
• הבנת הנקרא של כמה משפטים (MultiRC)
• מערך נתונים של הבנת הנקרא עם חשיבה רציונלית שמבוססת על שכל ישר (ReCoRD)
• Recognizing Textual Entailment (RTE)
• מילים בהקשר (WiC)
• Winograd Schema Challenge (WSC)

פרטים נוספים זמינים במאמר SuperGLUE: A Stickier Benchmark for General-Purpose Language Understanding Systems.

T

הפסד בבדיקה

#fundamentals

#Metric

מדד שמייצג את ההפסד של מודל בהשוואה לקבוצת נתונים לבדיקה. כשבונים מודל, בדרך כלל מנסים לצמצם את הפסד הבדיקה. הסיבה לכך היא שערך נמוך של הפסד בבדיקה הוא אות איכות חזק יותר מערך נמוך של הפסד באימון או ערך נמוך של הפסד באימות.

פער גדול בין הפסד הבדיקה לבין הפסד האימון או הפסד האימות מצביע לפעמים על הצורך להגדיל את שיעור הרגולריזציה.

דיוק top-k

#Metric

אחוז הפעמים שבהן 'תווית היעד' מופיעה בתוך k המיקומים הראשונים של רשימות שנוצרו. הרשימות יכולות להיות המלצות מותאמות אישית או רשימה של פריטים שמסודרים לפי softmax.

דיוק k המובילים נקרא גם דיוק ב-k.

הערה: תווית היעד יכולה להיות כל מחלקה (לא בהכרח מחלקת אמת הקרקע), ולכן דיוק k-העליון לא תמיד שווה לדיוק מסורתי.

לוחצים על הסמל כדי לראות דוגמה.

נניח שיש מערכת למידת מכונה שמשתמשת ב-softmax כדי לזהות הסתברויות של עצים על סמך תמונה של עלי עצים. בטבלה הבאה מוצגות רשימות פלט שנוצרו מחמש תמונות של עצים כקלט. כל שורה מכילה תווית יעד וחמישה עצים עם הסבירות הגבוהה ביותר. לדוגמה, אם תווית היעד הייתה maple, מודל למידת המכונה זיהה את elm כעץ הכי סביר, את oak כעץ השני הכי סביר וכן הלאה.

תווית היעד	1	2	3	4	5
מייפל	בוקיצה	אלון	maple	אשור	צפצפה
קרנית	אלון	dogwood	צפצפה	Hickory	מייפל
אלון	oak	טיליה	ארבה	אלמון	Linden
Linden	מייפל	פפאיה	אלון	טיליה	צפצפה
אלון	ארבה	Linden	oak	מייפל	פפאיה

תווית היעד מופיעה במיקום הראשון רק פעם אחת, ולכן דיוק המיקום הראשון הוא:

$$\text{top-1 accuracy} = \frac{\text{1}} {\text{5}} = 0.2$$

תווית היעד מופיעה באחד משלושת המיקומים הראשונים ארבע פעמים, לכן רמת הדיוק של 3 המיקומים הראשונים היא:

$$\text{top-1 accuracy} = \frac{\text{4}} {\text{5}} = 0.8$$

---

תוכן רעיל

#Metric

המידה שבה התוכן פוגעני, מאיים או מעליב. מודלים רבים של למידת מכונה יכולים לזהות, למדוד ולסווג רעילות. רוב המודלים האלה מזהים רעילות לפי כמה פרמטרים, כמו רמת השפה הפוגענית ורמת השפה המאיימת.

הפסד האימון

#fundamentals

#Metric

מדד שמייצג את האובדן של מודל במהלך איטרציה מסוימת של אימון. לדוגמה, נניח שפונקציית ההפסד היא Mean Squared Error. יכול להיות שההפסד של האימון (השגיאה הממוצעת בריבוע) באיטרציה העשירית הוא 2.2, וההפסד של האימון באיטרציה ה-100 הוא 1.9.

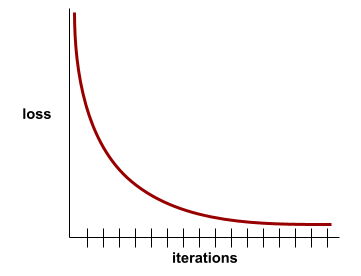
בעקומת הפסד מוצג הפסד האימון לעומת מספר האיטרציות. עקומת הפסד מספקת את הרמזים הבאים לגבי האימון:

• שיפוע כלפי מטה מעיד על שיפור במודל.
• שיפוע כלפי מעלה מרמז שהמודל הולך ונעשה גרוע יותר.
• שיפוע מתון מעיד שהמודל הגיע להתכנסות.

לדוגמה, עקומת ההפסד הבאה היא אידיאלית במידה מסוימת, והיא מציגה:

• שיפוע חד כלפי מטה במהלך האיטרציות הראשוניות, שמצביע על שיפור מהיר של המודל.
• שיפוע שמשתטח בהדרגה (אבל עדיין יורד) עד לסיום האימון, מה שמצביע על שיפור מתמשך של המודל בקצב איטי יותר מאשר במהלך האיטרציות הראשוניות.
• שיפוע מתון לקראת סוף האימון, שמצביע על התכנסות.

למרות שחשוב להבין את הפסדי האימון, כדאי גם לעיין במושג הכללה.

מענה על שאלות טריוויה

#Metric

מערכי נתונים להערכת היכולת של מודל שפה גדול לענות על שאלות טריוויה. כל מערך נתונים מכיל זוגות של שאלות ותשובות שנכתבו על ידי חובבי טריוויה. מערכי נתונים שונים מבוססים על מקורות שונים, כולל:

• חיפוש באינטרנט (TriviaQA)
• ויקיפדיה (TriviaQA_wiki)

מידע נוסף זמין במאמר TriviaQA: A Large Scale Distantly Supervised Challenge Dataset for Reading Comprehension.

TRUE שלילי (TN)

#fundamentals

#Metric

דוגמה שבה המודל מנבא בצורה נכונה את הסיווג השלילי. לדוגמה, המודל מסיק שהודעת אימייל מסוימת היא לא ספאם, והודעת האימייל הזו באמת לא ספאם.

חיובי אמיתי (TP)

#fundamentals

#Metric

דוגמה שבה המודל מנבא בצורה נכונה את הסיווג החיובי. לדוגמה, המודל מסיק שהודעת אימייל מסוימת היא ספאם, והודעת האימייל הזו באמת ספאם.

שיעור החיוביים האמיתיים (TPR)

#fundamentals

#Metric

מילה נרדפת לrecall. כלומר:

$$\text{true positive rate} = \frac {\text{true positives}} {\text{true positives} + \text{false negatives}}$$

שיעור החיוביים האמיתיים הוא ציר ה-y בעקומת ROC.

מענה לשאלות בשפות שונות (TyDi QA)

#Metric

מערך נתונים גדול להערכת רמת המיומנות של מודל LLM במתן תשובות לשאלות. מערך הנתונים מכיל זוגות של שאלות ותשובות בשפות רבות.

פרטים נוספים זמינים במאמר TyDi QA: A Benchmark for Information-Seeking Question Answering in Typologically Diverse Languages.

V

הפסד אימות

#fundamentals

#Metric

מדד שמייצג את ההפסד של מודל בקבוצת נתונים לתיקוף במהלך איטרציה מסוימת של אימון.

אפשר לעיין גם בעקומת הכללה.

חשיבות המשתנים

#df

#Metric

קבוצת ציונים שמציינת את החשיבות היחסית של כל תכונה למודל.

לדוגמה, נניח שיש עץ החלטה שמבצע הערכה של מחירי בתים. נניח שעץ ההחלטה הזה משתמש בשלושה מאפיינים: גודל, גיל וסגנון. אם קבוצת חשיבות המשתנים של שלושת המאפיינים היא {size=5.8, age=2.5, style=4.7}, אז המאפיין size חשוב יותר לעץ ההחלטה מהמאפיינים age או style.

קיימים מדדים שונים לחשיבות משתנים, שיכולים לספק למומחי למידת מכונה מידע על היבטים שונים של מודלים.

W

פונקציית הפסד Wasserstein

#Metric

אחת מפונקציות ההפסד שבהן נעשה שימוש בדרך כלל ברשתות יריבות גנרטיביות, על סמך המרחק בין חלוקת הנתונים שנוצרו לבין הנתונים האמיתיים.

WiC

#Metric

קיצור למילים בהקשר.

WikiLingua (wiki_lingua)

#Metric

מערך נתונים להערכת היכולת של מודל LLM לסכם מאמרים קצרים. ‫WikiHow, אנציקלופדיה של מאמרים שמסבירים איך לבצע משימות שונות, הוא המקור שנכתב על ידי בני אדם גם למאמרים וגם לסיכומים. כל רשומה במערך הנתונים כוללת:

• מאמר שנוצר על ידי הוספה של כל שלב בגרסת הפרוזה (הפסקה) של הרשימה הממוספרת, ללא משפט הפתיחה של כל שלב.
• סיכום של המאמר, שמורכב ממשפט הפתיחה של כל שלב ברשימה הממוספרת.

פרטים נוספים זמינים במאמר WikiLingua: A New Benchmark Dataset for Cross-Lingual Abstractive Summarization.

אתגר סכימת וינוגרד (WSC)

#Metric

פורמט (או מערך נתונים שתואם לפורמט הזה) להערכת היכולת של מודל שפה גדול (LLM) לקבוע את הצירוף הנומינלי שאליו מתייחסת מילת גוף.

כל רשומה באתגר סכימת וינוגרד כוללת:

• פסקה קצרה שמכילה כינוי גוף של יעד
• כינוי גוף ליעד
• צירופי שם עצם אפשריים, ואחריהם התשובה הנכונה (ערך בוליאני). אם כינוי הגוף שאליו מתייחסים מתייחס למועמד הזה, התשובה היא True. אם כינוי הגוף לא מתייחס למועמד הזה, התשובה היא False.

לדוגמה:

• פסקה: Mark told Pete many lies about himself, which Pete included in his book. הוא היה צריך להיות יותר כנה.
• כינוי הגוף הממוקד: הוא
• צירופי שם עצם מוצעים:
  • סימון: True, כי כינוי הגוף המטורגט מתייחס למארק
  • פיט: False, כי כינוי הגוף לא מתייחס לפיט

אתגר סכמת וינוגרד הוא רכיב של SuperGLUE.

מילים בהקשר (WiC)

#Metric

מערך נתונים להערכת היכולת של LLM להשתמש בהקשר כדי להבין מילים שיש להן כמה משמעויות. כל רשומה במערך הנתונים מכילה:

• שני משפטים, שכל אחד מהם מכיל את מילת היעד
• מילת היעד
• התשובה הנכונה (ערך בוליאני), כאשר:
  • הערך True מציין שלמילה המטרה יש את אותה משמעות בשני המשפטים
  • הערך False מציין שלמילה המטרה יש משמעות שונה בשני המשפטים

לדוגמה:

• שני משפטים:
  • יש הרבה אשפה בקרקעית הנהר.
  • אני תמיד מניח מים ליד המיטה כשאני הולך לישון.
• מילת היעד: bed
• תשובה נכונה: False, כי למילת היעד יש משמעות שונה בשני המשפטים.

פרטים נוספים זמינים במאמר WiC: the Word-in-Context Dataset for Evaluating Context-Sensitive Meaning Representations.

‫Words in Context הוא רכיב של SuperGLUE ensemble.

WSC

#Metric

קיצור של Winograd Schema Challenge (אתגר סכימת וינוגרד).

X

‫XL-Sum (xlsum)

#Metric

מערך נתונים להערכת רמת המיומנות של מודל שפה גדול (LLM) בסיכום טקסט. ‫XL-Sum מספק רשומות בשפות רבות. כל רשומה במערך הנתונים מכילה:

• מאמר שנלקח מ-British Broadcasting Company‏ (BBC).
• סיכום של המאמר שנכתב על ידי מחבר המאמר. שימו לב שהסיכום יכול להכיל מילים או ביטויים שלא מופיעים במאמר.

פרטים נוספים זמינים במאמר XL-Sum: Large-Scale Multilingual Abstractive Summarization for 44 Languages (סיכום מופשט רב-לשוני בקנה מידה גדול ל-44 שפות).