Ta strona zawiera hasła z gloszariu modelu Image Models. Aby poznać wszystkie terminy z glosariusza, kliknij tutaj.
A
rzeczywistość rozszerzona
Technologia, która nakłada obraz wygenerowany komputerowo na widok świata widziany przez użytkownika, tworząc w ten sposób obraz złożony.
autoencoder
System, który uczy się wyodrębniać najważniejsze informacje z danych wejściowych. Autoenkodery to połączenie enkodera i dekodera. Autoenkodery działają w ramach następującego dwuetapowego procesu:
- Koder mapuje dane wejściowe na (zazwyczaj) stratny format o mniejszej wymiarowości (pośredni).
- Dekoder tworzy wersję pierwotnego wejścia z utratą jakości, mapując format o niższej wymiarowości na pierwotny format wejściowy o wyższej wymiarowości.
Autoenkodery są trenowane kompleksowo, a dekodery próbują odtworzyć oryginalne dane wejściowe z pośredniego formatu kodowania w jak najwierniejszy sposób. Ponieważ format pośredni jest mniejszy (ma mniejszą wymiarność) niż format oryginalny, autoencoder musi się nauczyć, które informacje wejściowe są niezbędne, a wyjście nie będzie dokładnie takie samo jak dane wejściowe.
Na przykład:
- Jeśli dane wejściowe to grafika, kopia nieścisła będzie podobna do oryginalnej grafiki, ale nieco zmodyfikowana. Być może kopia niepełna usuwa szum z pierwotnej grafiki lub wypełnia brakujące piksele.
- Jeśli dane wejściowe to tekst, autoencoder wygeneruje nowy tekst, który będzie naśladował (ale nie będzie identyczny) z oryginałem.
Zobacz też wariacyjne autoenkodery.
model autoregresyjny
model, który wyprowadza prognozę na podstawie swoich poprzednich prognoz. Na przykład autoregresyjne modele językowe przewidują następny token na podstawie wcześniej przewidzianych tokenów. Wszystkie duże modele językowe oparte na transformerach są autoregresyjne.
Z kolei modele obrazów oparte na GAN zwykle nie są autoregresywne, ponieważ generują obraz w jednym przejęciu do przodu, a nie w kolejnych krokach. Niektóre modele do generowania obrazów są autoregresyjne, ponieważ generują obraz krok po kroku.
B
ramka ograniczająca
Na obrazie współrzędne (x, y) prostokąta wokół obszaru zainteresowania, np. psa na obrazie poniżej.

C
splotu
W matematyce, potocznie, mieszanka 2 funkcji. W uczeniu maszynowym konwolucja łączy konwolucyjny filtr z macierzą wejściową, aby wytrenować wagi.
Termin „konwolucja” w uczeniu maszynowym często oznacza operację konwolucyjną lub warstwę konwolucyjną.
Bez splotów algorytm systemów uczących się musiałby nauczyć się osobnego wagi dla każdej komórki w dużym tensorze. Na przykład algorytm uczenia maszynowego trenowany na obrazach 2K x 2K musiałby znaleźć 4 mln oddzielnych wag. Dzięki konwolucjom algorytm uczenia maszynowego musi tylko znaleźć wagi dla każdej komórki w filtrze konwolutywnym, co znacznie zmniejsza ilość pamięci potrzebnej do trenowania modelu. Gdy zastosujesz filtr konwolucyjny, zostanie on po prostu powielony w komórkach, tak aby każda z nich została pomnożona przez filtr.
Więcej informacji znajdziesz w Introducing Convolutional Neural Networks (Wprowadzenie do konwolucyjnych sieci neuronowych) w kursie Klasyfikacja obrazów.
filtr konwolucyjny
Jeden z 2 elementów w operacji konwolucyjnej. (Drugi aktor to wycinek macierzy wejściowej). Filtr konwolucyjny to macierz o tym samym rangu co macierz wejściowa, ale o mniejszym kształcie. Na przykład w przypadku macierzy wejściowej 28 x 28 filtr może być dowolną macierzą 2D mniejszą niż 28 x 28.
W przypadku manipulacji fotograficznej wszystkie komórki w filtrze konwolutacji są zwykle ustawione na stały wzór jedynek i zer. W uczeniu maszynowym filtry konwolucyjne są zwykle zasilane losowymi liczbami, a następnie sieć trenowana dobiera optymalne wartości.
Więcej informacji znajdziesz w części Konwolucja kursu Klasyfikacja obrazów.
warstwa konwolucyjna
Warstwa głębokiej sieci neuronowej, w której splotowy filtr przetwarza wejściową macierz. Weź pod uwagę na przykład ten filtr koniunkcyjny o wymiarach 3 x 3:
![Macierz 3 x 3 z tymi wartościami: [[0,1,0], [1,0,1], [0,1,0]]](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalFilter33.svg?authuser=2&hl=pl)
Animacja poniżej przedstawia warstwę konwolucyjną składającą się z 9 operacji konwolucyjnych z użyciem wejściowej macierzy 5 x 5. Zwróć uwagę, że każda operacja konwolucyjna działa na innym kawałku 3 × 3 macierzy wejściowej. Wynikowa macierz 3 x 3 (po prawej) składa się z wyników 9 operacji konwolucyjnych:
![Animacja przedstawiająca 2 macierz. Pierwsza to macierz 5 × 5: [[128,97,53,201,198], [35,22,25,200,195],
[37,24,28,197,182], [33,28,92,195,179], [31,40,100,192,177]].
Druga to macierz 3 x 3:[[181,303,618], [115,338,605], [169,351,560]].
Druga matryca jest obliczana przez zastosowanie filtra convolacyjnego [[0, 1, 0], [1, 0, 1], [0, 1, 0]] do różnych podzbiorów 3 x 3 macierzy 5 x 5.](https://developers.google.com/static/machine-learning/glossary/images/AnimatedConvolution.gif?authuser=2&hl=pl)
Więcej informacji znajdziesz w sekcji Pełno połączone warstwy w Kursie klasyfikacji obrazów.
konwolucyjna sieć neuronowa
Sieci neuronowej, w której co najmniej 1 warstwa jest warstwą konwolucyjną. Typowa sieć neuronowa konwolucyjna składa się z pewnej kombinacji tych warstw:
Splotowe sieci neuronowe bardzo dobrze sprawdzają się w rozwiązywaniu niektórych problemów, takich jak rozpoznawanie obrazów.
operacja splotu
Następująca dwuetapowa operacja matematyczna:
- Element-wise multiplication of the convolutional filter and a slice of an input matrix. (wycinek macierzy wejściowej ma ten sam wymiar i rozmiar co filtr konwolucyjny).
- Suma wszystkich wartości w wynikającej z tego macierzy wynikowej.
Weźmy na przykład tę macierz wejściową 5 x 5:
![Macierz 5 x 5: [[128,97,53,201,198], [35,22,25,200,195],
[37,24,28,197,182], [33,28,92,195,179], [31,40,100,192,177]].](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerInputMatrix.svg?authuser=2&hl=pl)
Wyobraź sobie teraz ten filtr splotowy 2 x 2:
![Matryca 2 x 2: [[1, 0], [0, 1]]](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerFilter.svg?authuser=2&hl=pl)
Każda operacja konwolucyjna obejmuje jeden wycinek 2 x 2 z macierzy wejściowej. Załóżmy na przykład, że używamy wycinka 2 x 2 w lewym górnym rogu macierzy wejściowej. Operacja splotu na tym kawałku wygląda tak:
![Zastosowanie filtra konwolucyjnego [[1, 0], [0, 1]] do lewego górnego narożnika
sekcji 2 x 2 macierzy wejściowej, która ma postać [[128,97], [35,22]].
Filtr konwolucyjny pozostawia wartości 128 i 22 bez zmian, ale ustawia na 0 wartości 97 i 35. W związku z tym operacja sprzężenia daje wartość 150 (128 + 22).](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerOperation.svg?authuser=2&hl=pl)
Warstwa konwolucyjna składa się z szeregu operacji konwolucyjnych, z których każda działa na innym fragmencie macierzy wejściowej.
D
wzbogacanie danych
Sztuczne zwiększanie zakresu i liczby przykładów treningowych przez przekształcanie dotychczasowych przykładów w celu utworzenia dodatkowych przykładów. Załóżmy na przykład, że obrazy są jedną z właściwości, ale Twój zbiór danych nie zawiera wystarczającej liczby przykładów obrazów, aby model mógł się nauczyć przydatnych skojarzeń. W idealnej sytuacji do zbioru danych należy dodać wystarczającą liczbę oznaczonych obrazów, aby umożliwić prawidłowe trenowanie modelu. Jeśli nie jest to możliwe, rozszerzanie danych może obracać, rozciągać i odbywać odbicia lustrzane każdego obrazu, aby wygenerować wiele wersji oryginalnego zdjęcia. Dzięki temu można uzyskać wystarczającą ilość danych z oznacznikami, aby umożliwić skuteczne przeszkolenie.
splotowa sieć neuronowa z separowanymi filtrami (sepCNN)
Architektura sieci neuronowej z konwolucją oparta na Inception, ale z zastosowaniem modułów Inception zastąpionych konwolucjami rozdzielanymi głębokościowo. Inna nazwa to Xception.
Konwolucja rozdzielna w głębi (nazywana też konwolucją rozdzielną) dzieli standardową konwolucję 3D na 2 oddzielne operacje konwolucji, które są bardziej wydajne pod względem obliczeniowym: najpierw konwolucję w głębi o głębokości 1 (n × n × 1), a potem konwolucję punktową o długości i szerokości 1 (1 × 1 × n).
Więcej informacji znajdziesz w artykule Xception: Deep Learning with Depthwise Separable Convolutions.
downsampling
Termin z przeciążeniem, który może oznaczać:
- Zmniejszenie ilości informacji w cechu, aby trenować model w bardziej efektywny sposób. Na przykład przed wytrenowaniem modelu do rozpoznawania obrazów zmniejsz rozdzielczość zdjęć o wysokiej rozdzielczości do formatu o niższej rozdzielczości.
- trenowanie na przykładach o nieproporcjonalnie niskim odsetku nadreprezentowanych klas, aby poprawić trenowanie modelu na przykładach z klas o niedostatecznie dużej reprezentacji; Na przykład w zbiorze danych z niezrównowagą klas modele zwykle dużo się uczą o klasie większościowej, ale niewystarczająco dużo o klasie mniejszościowej. Próbkowanie w dół pomaga zrównoważyć ilość treningu w klasach większościowych i mniejszościowych.
Więcej informacji znajdziesz w sekcji Zbiory danych: nierównowaga w zbiorach danych w szybkim szkoleniu z uczenia maszynowego.
F
dostrojenie
Drugi przejazd treningowy, który jest wykonywany na wytrenowanym wcześniej modelu w celu dostosowania jego parametrów do konkretnego zastosowania. Przykładowa pełna sekwencja trenowania niektórych dużych modeli językowych:
- Wstępne trenowanie: trenowanie dużego modelu językowego na ogromnym ogólnym zbiorze danych, takim jak wszystkie strony Wikipedii w języku angielskim.
- Dostosowywanie: wytrenowanie wstępnie wytrenowanego modelu do wykonywania konkretnego zadania, np. odpowiadania na pytania medyczne. Dostrojenie polega zwykle na wykorzystaniu setek lub tysięcy przykładów dotyczących konkretnego zadania.
Innym przykładem jest pełna sekwencja trenowania dużego modelu obrazu:
- Wstępne trenowanie: trenowanie dużego modelu obrazów na olbrzymim ogólnym zbiorze danych, takim jak wszystkie obrazy w Wikimedia Commons.
- Dostrojenie: wytrenowanie wstępnie przeszkolonego modelu do wykonywania konkretnego zadania, np. generowania obrazów orek.
Dostosowanie dokładne może obejmować dowolną kombinację tych strategii:
- zmodyfikować wszystkie istniejące parametry wytrenowanego wcześniej modelu; Czasami nazywa się to pełnym dostrojeniem.
- Modyfikowanie tylko niektórych dotychczasowych parametrów w modelu wstępnie wytrenowanym (zazwyczaj warstw najbliżej warstwy wyjściowej), przy zachowaniu innych dotychczasowych parametrów (zazwyczaj warstw najbliżej wejściowej warstwy). Zobacz dostrajanie z uwzględnieniem wydajności.
- Dodawanie kolejnych warstw, zwykle na wierzchu istniejących warstw najbliżej warstwy wyjściowej.
Dostrojenie to forma uczenia się przez przenoszenie. W ramach dostrojenia można użyć innej funkcji utraty lub innego typu modelu niż te, które zostały użyte do trenowania wstępnie wytrenowanego modelu. Możesz na przykład dostosować wstępnie wytrenowany model dużych obrazów, aby uzyskać model regresji zwracający liczbę ptaków na obrazie wejściowym.
Porównaj dostosowanie do tych terminów:
Więcej informacji znajdziesz w części Dostrojenie w Szybkim szkoleniu z uczenia maszynowego.
G
Gemini
Ekosystem obejmujący najbardziej zaawansowaną AI od Google. Elementy tego ekosystemu:
- Różne modele Gemini.
- Interaktywny interfejs konwersacyjny do modelu Gemini. Użytkownicy wpisują prompty, a Gemini na nie odpowiada.
- różne interfejsy Gemini API.
- różne usługi biznesowe oparte na modelach Gemini, np. Gemini dla Google Cloud.
Modele Gemini
Najnowocześniejsze modele multimodalne oparte na Transformerze od Google. Modele Gemini zostały zaprojektowane specjalnie do integracji z agentami.
Użytkownicy mogą wchodzić w interakcje z modelami Gemini na różne sposoby, m.in. za pomocą interaktywnego interfejsu dialogowego i pakietów SDK.
generatywnej AI
Nowe, rewolucyjne pole, które nie ma formalnej definicji. Większość ekspertów zgadza się jednak, że modele generatywnej AI mogą tworzyć („generować”) treści, które:
- złożone
- spójny
- oryginał
Na przykład model generatywnej AI może tworzyć zaawansowane eseje lub obrazy.
Niektóre starsze technologie, w tym sieci LSTM i sieci RNN, również mogą generować oryginalne i spójne treści. Niektórzy eksperci uważają, że te wcześniejsze technologie są generatywną AI, podczas gdy inni uważają, że prawdziwa generatywna AI wymaga bardziej złożonego wyjścia niż te wcześniejsze technologie.
W przeciwieństwie do systemów ML prognozujących.
I
rozpoznawanie obrazów
Proces klasyfikowania obiektów, wzorów lub pojęć na obrazie. Rozpoznawanie obrazów to także klasyfikacja obrazów.
Więcej informacji znajdziesz w artykule ML Practicum: Image Classification.
Więcej informacji znajdziesz w praktycznym kursie dotyczącym uczenia maszynowego: klasyfikacja obrazów.
współczynnik podobieństwa (IoU)
Przecięcie 2 zbiorów podzielone przez ich związek. W zadaniach związanych z wykrywaniem obrazów za pomocą uczenia maszynowego współczynnik podobieństwa służy do pomiaru dokładności prognozowanej ramki ograniczającej modelu w odniesieniu do ramki ograniczającej danych podstawowych. W tym przypadku współczynnik podobieństwa dla dwóch pól to stosunek obszaru nakładania się do całkowitego obszaru, a jego wartość waha się od 0 (brak nakładania się prognozowanej ramki ograniczającej i ramki ograniczającej danych podstawowych) do 1 (prognozowana i dane podstawowe mają dokładnie te same współrzędne).
Na przykład na obrazie poniżej:
- Zaznaczony na fioletowo jest ramka ograniczająca (współrzędne określające, gdzie według modelu znajduje się nocny stolik na obrazie).
- Zaznaczony na zielono jest obszar ograniczony (box) danych podstawowych (współrzędne określające, gdzie na obrazie znajduje się stół nocny).
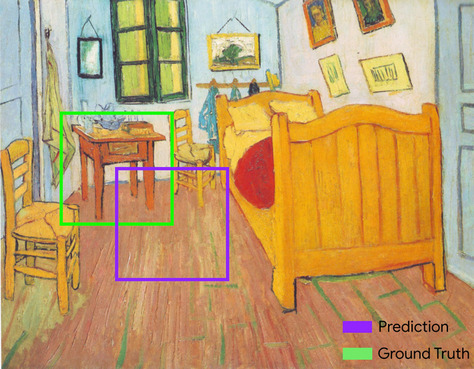
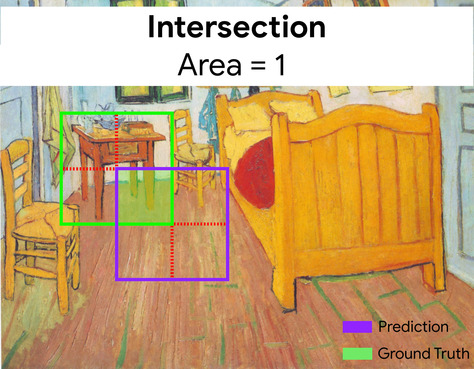
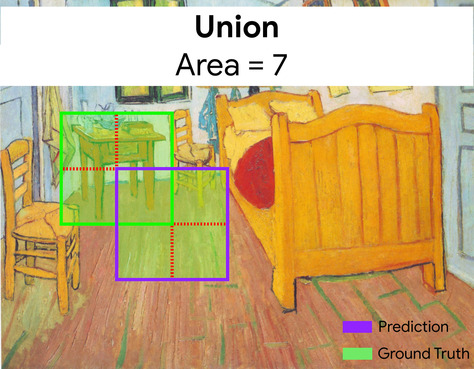
Współczynnik podobieństwa ramek ograniczających prognozy i danych podstawowych (po lewej stronie na dole) wynosi 1, a suma ramek ograniczających prognozy i danych podstawowych (po prawej stronie na dole) wynosi 7, więc współczynnik podobieństwa to \(\frac{1}{7}\).
K
keypoints
współrzędne poszczególnych elementów na obrazie; Na przykład w przypadku modelu rozpoznawania obrazów, który rozróżnia gatunki kwiatów, punktami kluczowymi mogą być środek każdego płatka, łodyga, pręciki itp.
L
punkty orientacyjne
Synonim punktów stycznych.
M
MMIT
Skrót od multimodal instruction-tuned.
MNIST
Dane publicznie dostępne, zebrane przez LeCuna, Cortesa i Burgesa,zawierające 60 tys. obrazów. Każdy obraz pokazuje, jak człowiek ręcznie napisał daną cyfrę w zakresie 0–9. Każdy obraz jest przechowywany jako tablica liczb całkowitych 28 x 28, gdzie każda liczba całkowita to wartość w skali szarości z zakresu od 0 do 255 włącznie.
MNIST to kanoniczny zbiór danych do uczenia maszynowego, który jest często używany do testowania nowych metod uczenia maszynowego. Więcej informacji znajdziesz w bazie danych MNIST z odręcznie napisanymi cyframi.
MOE
Skrót od mixture of experts.
P
wspólne korzystanie
Redukcja macierzy (lub macierz) utworzonych przez wcześniejszy warstw convolacyjną do mniejszej macierzy. Zbiorcze zliczanie zwykle polega na przyjęciu wartości maksymalnej lub średniej w zbiorczym obszarze. Załóżmy na przykład, że mamy taką oto macierz 3 x 3:
![Macierz 3 x 3: [[5,3,1], [8,2,5], [9,4,3]].](https://developers.google.com/static/machine-learning/glossary/images/PoolingStart.svg?authuser=2&hl=pl)
Operacja zliczania, podobnie jak operacja konwolucyjna, dzieli tę macierz na części i przesuwa tę operację konwolucyjną o krok. Załóżmy na przykład, że operacja zliczania dzieli macierz konwolucyjną na części 2 x 2 o skoku 1 x 1. Jak widać na diagramie poniżej, występują 4 operacje łączenia. Załóżmy, że każda operacja zgrupowania wybiera maksymalną wartość 4 elementów w danym przekroju:
![Wejściem jest macierz 3 x 3 o wartościach: [[5,3,1], [8,2,5], [9,4,3]].
Lewostronna podmacierz 2 × 2 macierzy wejściowej ma postać [[5,3], [8,2]], więc operacja zliczania w lewym górnym rogu daje wartość 8 (która jest maksymalną wartością z 5, 3, 8 i 2). Prawy górny podmacierz 2 × 2 macierzy wejściowej ma postać [[3,1], [2,5]], więc operacja zliczania w prawym górnym rogu daje wartość 5. Lewo-doły macierz podrzędna o wymiarach 2 × 2 ma postać [[8,2], [9,4]], więc operacja zliczania w lewym dolnym rogu zwraca wartość 9. Prawy dolny podmacierz 2 × 2 macierzy wejściowej ma postać [[2,5], [4,3]], więc operacja zliczania w prawym dolnym rogu zwraca wartość 5. Podsumowując, operacja zliczania daje macierz 2 x 2: [[8,5], [9,5]].](https://developers.google.com/static/machine-learning/glossary/images/PoolingConvolution.svg?authuser=2&hl=pl)
Połączenie pomaga zapewnić niezmienność w translacji w macierz wejściowej.
Zbiory danych w przypadku aplikacji do przetwarzania obrazu są bardziej formalnie nazywane zbiorami danych przestrzennych. W przypadku aplikacji wykorzystujących dane czasowe złączanie nazywa się zwykle złączaniem czasowym. W mniej formalnym ujęciu zgrupowanie jest często nazywane podpróbkowaniem lub próbkowaniem w dół.
Zapoznaj się z konwolucyjnymi sieciami neuronowymi w szkoleniu ML Practicum: klasyfikacja obrazów.
model po trenowaniu
Luźno zdefiniowany termin, który zwykle odnosi się do wytrenowanego modelu, który przeszedł pewien proces przetwarzania, np. jeden z tych:
wytrenowany model
Zwykle jest to model, który został już wytrenowany. Termin ten może też oznaczać wcześniej wytrenowany wektor zanurzeniowy.
Termin wstępnie wytrenowany model językowy zwykle odnosi się do już wytrenowanych dużych modeli językowych.
przed treningiem
Wstępne trenowanie modelu na dużym zbiorze danych. Niektóre wytrenowane wstępnie modele są niezgrabnymi olbrzymami i zwykle trzeba je dopracować, przeprowadzając dodatkowe szkolenie. Na przykład eksperci od uczenia maszynowego mogą wstępnie wytrenować duży model językowy na podstawie ogromnego zbioru danych tekstowych, takiego jak wszystkie strony w języku angielskim w Wikipedii. Po wstępnym trenowaniu model może zostać dopracowany za pomocą jednej z tych technik:
- distillation
- dokładne dopasowanie,
- dostrajanie instrukcji
- dostrajanie z optymalnym wykorzystaniem parametrów
- prompt-tuning
R
niezmienniczość obrotowa
W przypadku problemu klasyfikacji obrazów chodzi o zdolność algorytmu do prawidłowej klasyfikacji obrazów nawet wtedy, gdy zmienia się ich orientacja. Na przykład algorytm nadal może rozpoznać rakietę tenisową, niezależnie od tego, czy jest skierowana w górę, w bok czy w dół. Pamiętaj, że odporność na obrót nie zawsze jest pożądana. Na przykład odwrócona cyfra 9 nie powinna być klasyfikowana jako cyfra 9.
Zobacz też niezmienność w translacji i niezmienność w skali.
S
niezmienność rozmiaru
W przypadku problemu klasyfikacji obrazów chodzi o zdolność algorytmu do prawidłowej klasyfikacji obrazów nawet wtedy, gdy zmienia się ich rozmiar. Na przykład algorytm nadal rozpoznaje kota, niezależnie od tego, czy zajmuje on 2 mln pikseli czy 200 tys. pikseli. Pamiętaj, że nawet najlepsze algorytmy klasyfikacji obrazów mają praktyczne ograniczenia dotyczące nieczułości na zmiany rozmiaru. Na przykład algorytm (ani człowiek) nie będzie w stanie prawidłowo sklasyfikować obrazu kota, który zajmuje tylko 20 pikseli.
Zobacz też niezmienność w przełożeniu i niezmienność w obrocie.
Więcej informacji znajdziesz w Kursie dotyczącym klasteringu.
agregacja przestrzenna
Zobacz pooling.
stride
W operacji konwolucji lub zgrupowaniu jest to delta w każdym wymiarze następnej serii kawałków danych wejściowych. Na przykład ta animacja pokazuje krok (1,1) podczas operacji konwolucyjnej. Dlatego następny plaster danych wejściowych zaczyna się o jedną pozycję w prawo od poprzedniego. Gdy operacja dotrze do prawej krawędzi, następny plaster będzie przesunięty w lewo, ale o jedną pozycję w dół.
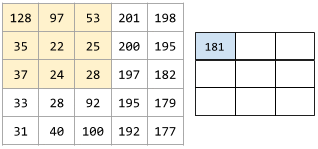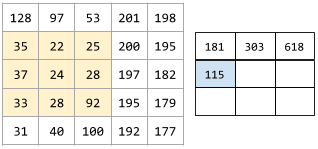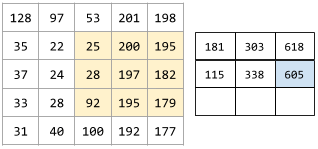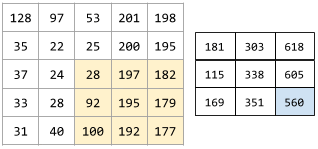
Poprzedni przykład pokazuje krok dwuwymiarowy. Jeśli wejściowa tablica jest trójwymiarowa, krok będzie też trójwymiarowy.
podpróbkowanie
Zobacz pooling.
T
temperatura
Hiperparametr, który kontroluje stopień losowości danych wyjściowych modelu. Wyższe temperatury powodują bardziej losowe wyniki, a niższe – mniej losowe.
Wybór najlepszej temperatury zależy od konkretnego zastosowania i preferowanych właściwości wyników modelu. Na przykład prawdopodobnie podniesiesz temperaturę, gdy tworzysz aplikację, która generuje kreacje. Z kolei, aby zwiększyć dokładność i spójność modelu, który klasyfikuje obrazy lub tekst, prawdopodobnie obniżysz temperaturę.
Temperatura jest często używana z softmaxem.
niezmienniczość w przełożeniu
W przypadku problemu klasyfikacji obrazów chodzi o zdolność algorytmu do prawidłowej klasyfikacji obrazów nawet wtedy, gdy pozycja obiektów na obrazie ulega zmianie. Na przykład algorytm może nadal rozpoznawać psa, niezależnie od tego, czy znajduje się w środku kadru, czy po lewej stronie.
Zobacz też niezmienność rozmiaru i niezmienność obrotu.
