Trang này chứa các thuật ngữ trong bảng chú giải về Rừng quyết định. Để xem tất cả các thuật ngữ trong bảng chú giải, hãy nhấp vào đây.
A
lấy mẫu thuộc tính
Một chiến thuật để huấn luyện rừng quyết định trong đó mỗi cây quyết định chỉ xem xét một tập hợp con ngẫu nhiên gồm các đặc điểm có thể có khi tìm hiểu điều kiện. Nhìn chung, một tập hợp con khác của các đối tượng được lấy mẫu cho mỗi nút. Ngược lại, khi huấn luyện một cây quyết định mà không lấy mẫu thuộc tính, tất cả các đặc điểm có thể có đều được xem xét cho từng nút.
điều kiện căn chỉnh theo trục
Trong cây quyết định, điều kiện chỉ liên quan đến một đặc điểm. Ví dụ: nếu area là một đối tượng, thì sau đây là điều kiện căn chỉnh theo trục:
area > 200
Tương phản với điều kiện xiên.
B
đóng gói
Một phương pháp để huấn luyện một tập hợp trong đó mỗi mô hình thành phần huấn luyện trên một tập hợp con ngẫu nhiên của các ví dụ huấn luyện được lấy mẫu có thay thế. Ví dụ: rừng ngẫu nhiên là một tập hợp các cây quyết định được huấn luyện bằng phương pháp lấy mẫu lại.
Thuật ngữ bagging là viết tắt của bootstrap aggregating (tập hợp khởi động).
Hãy xem phần Rừng ngẫu nhiên trong khoá học Rừng quyết định để biết thêm thông tin.
điều kiện nhị phân
Trong cây quyết định, điều kiện chỉ có 2 kết quả có thể xảy ra, thường là có hoặc không. Ví dụ: sau đây là một điều kiện nhị phân:
temperature >= 100
Tương phản với điều kiện không phải là nhị phân.
Hãy xem Các loại điều kiện trong khoá học Rừng quyết định để biết thêm thông tin.
C
điều kiện
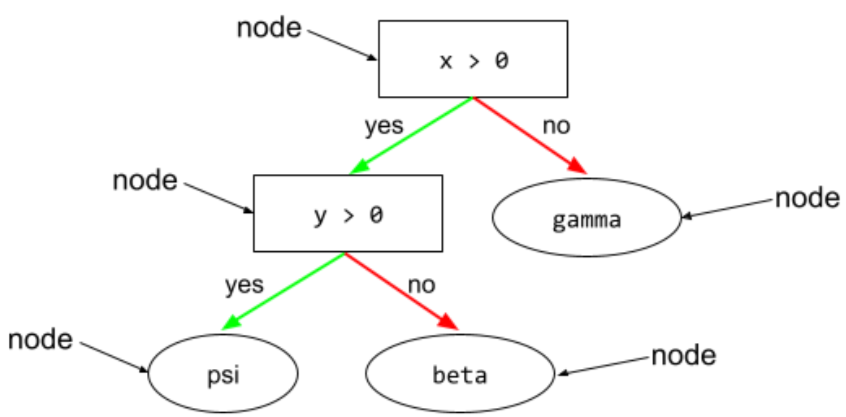
Trong cây quyết định, mọi nút đều thực hiện một kiểm thử. Ví dụ: cây quyết định sau đây có 2 điều kiện:
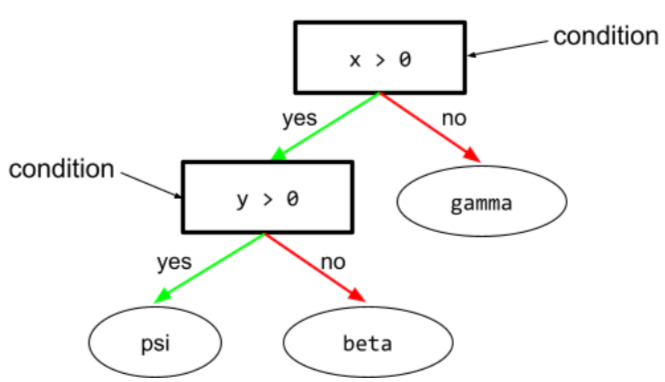
Điều kiện còn được gọi là phân tách hoặc kiểm thử.
Điều kiện tương phản với lá.
Xem thêm:
Hãy xem Các loại điều kiện trong khoá học Rừng quyết định để biết thêm thông tin.
D
rừng quyết định
Một mô hình được tạo từ nhiều cây quyết định. Rừng quyết định đưa ra dự đoán bằng cách tổng hợp các dự đoán của cây quyết định. Các loại rừng quyết định phổ biến bao gồm rừng ngẫu nhiên và cây được tăng cường độ dốc.
Hãy xem phần Rừng quyết định trong khoá học Rừng quyết định để biết thêm thông tin.
cây quyết định
Một mô hình học có giám sát bao gồm một tập hợp các điều kiện và các nút lá được sắp xếp theo hệ phân cấp. Ví dụ: sau đây là một cây quyết định:
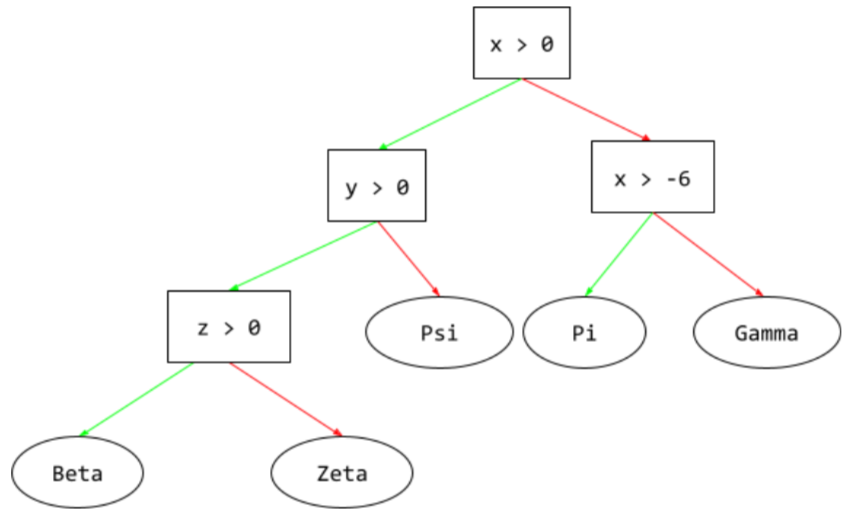
E
entropy
Trong lý thuyết thông tin, nội dung mô tả mức độ khó dự đoán của một phân phối xác suất. Ngoài ra, entropy cũng được xác định là lượng thông tin mà mỗi ví dụ chứa. Phân phối có entropy cao nhất có thể khi tất cả các giá trị của một biến ngẫu nhiên đều có khả năng xảy ra như nhau.
Độ đo hỗn loạn của một tập hợp có 2 giá trị có thể là "0" và "1" (ví dụ: nhãn trong bài toán phân loại nhị phân) có công thức sau:
H = -p log p – q log q = -p log p – (1-p) * log (1-p)
trong đó:
- H là entropy.
- p là phân số của "1" ví dụ.
- q là tỷ lệ của các ví dụ "0". Lưu ý rằng q = (1 – p)
- log thường là log2. Trong trường hợp này, đơn vị entropy là một bit.
Ví dụ: giả sử những điều sau đây:
- 100 ví dụ chứa giá trị "1"
- 300 ví dụ chứa giá trị "0"
Do đó, giá trị entropy là:
- p = 0,25
- q = 0,75
- H = (-0,25)log2(0,25) – (0,75)log2(0,75) = 0,81 bit cho mỗi ví dụ
Một tập hợp cân bằng hoàn hảo (ví dụ: 200 "0" và 200 "1") sẽ có độ đo entropy là 1 bit cho mỗi ví dụ. Khi một tập hợp trở nên mất cân bằng, entropy của tập hợp đó sẽ tiến về 0.0.
Trong cây quyết định, entropy giúp xây dựng mức tăng thông tin để giúp bộ phân tách chọn điều kiện trong quá trình phát triển cây quyết định phân loại.
So sánh entropy với:
- độ tinh khiết gini
- Hàm mất mát cross-entropy
Độ đo hỗn loạn thường được gọi là độ đo hỗn loạn của Shannon.
Hãy xem phần Bộ phân tách chính xác để phân loại nhị phân bằng các đặc điểm số trong khoá học Rừng quyết định để biết thêm thông tin.
F
tầm quan trọng của các đặc điểm
Từ đồng nghĩa với mức độ quan trọng của biến.
G
độ tinh khiết Gini
Một chỉ số tương tự như entropy. Trình phân tách sử dụng các giá trị bắt nguồn từ độ tinh khiết gini hoặc entropy để tạo điều kiện cho cây quyết định phân loại. Mức tăng thông tin được suy ra từ entropy. Không có thuật ngữ tương đương được chấp nhận rộng rãi cho chỉ số bắt nguồn từ độ tinh khiết Gini; tuy nhiên, chỉ số chưa được đặt tên này cũng quan trọng như mức tăng thông tin.
Độ tinh khiết Gini còn được gọi là chỉ số Gini hoặc đơn giản là Gini.
cây (quyết định) được tăng cường theo độ dốc (GBT)
Một loại rừng quyết định trong đó:
- Đào tạo dựa vào tăng cường độ dốc.
- Mô hình yếu là một cây quyết định.
Hãy xem bài viết Cây quyết định tăng cường độ dốc trong khoá học Rừng quyết định để biết thêm thông tin.
tăng cường độ dốc
Một thuật toán huấn luyện trong đó các mô hình yếu được huấn luyện để cải thiện chất lượng (giảm tổn thất) của một mô hình mạnh theo cách lặp đi lặp lại. Ví dụ: một mô hình yếu có thể là mô hình tuyến tính hoặc mô hình cây quyết định nhỏ. Mô hình mạnh sẽ là tổng của tất cả các mô hình yếu đã được huấn luyện trước đó.
Ở dạng đơn giản nhất của phương pháp tăng cường độ dốc, tại mỗi lần lặp lại, một mô hình yếu sẽ được huấn luyện để dự đoán độ dốc tổn thất của mô hình mạnh. Sau đó, đầu ra của mô hình mạnh được cập nhật bằng cách trừ đi độ dốc dự đoán, tương tự như phương pháp hạ độ dốc.
trong đó:
- $F_{0}$ là mô hình mạnh mẽ ban đầu.
- $F_{i+1}$ là mô hình mạnh tiếp theo.
- $F_{i}$ là mô hình mạnh hiện tại.
- $\xi$ là một giá trị nằm trong khoảng từ 0 đến 1, được gọi là hệ số thu hẹp, tương tự như tốc độ học trong phương pháp hạ độ dốc.
- $f_{i}$ là mô hình yếu được huấn luyện để dự đoán độ dốc tổn thất của $F_{i}$.
Các biến thể hiện đại của phương pháp tăng cường độ dốc cũng bao gồm đạo hàm bậc hai (Hessian) của tổn thất trong quá trình tính toán.
Cây quyết định thường được dùng làm mô hình yếu trong phương pháp tăng cường độ dốc. Xem cây (quyết định) được tăng cường độ dốc.
I
đường dẫn suy luận
Trong cây quyết định, trong quá trình suy luận, ví dụ cụ thể sẽ đi từ gốc đến các điều kiện khác, kết thúc bằng một nút lá. Ví dụ: trong cây quyết định sau đây, các mũi tên dày hơn cho thấy đường dẫn suy luận cho một ví dụ có các giá trị đặc điểm sau:
- x = 7
- y = 12
- z = -3
Đường dẫn suy luận trong hình minh hoạ sau đây đi qua 3 điều kiện trước khi đến nút lá (Zeta).
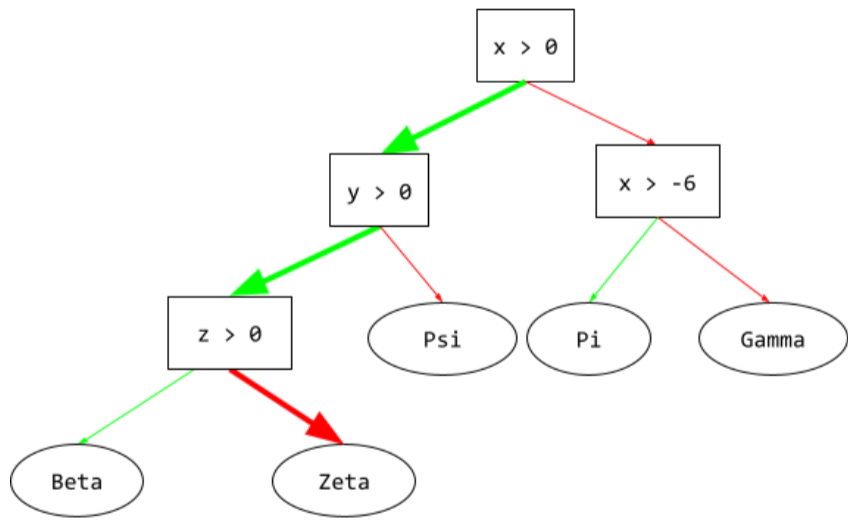
Ba mũi tên dày cho thấy đường suy luận.
Hãy xem Cây quyết định trong khoá học Rừng quyết định để biết thêm thông tin.
mức tăng thông tin
Trong rừng quyết định, sự khác biệt giữa entropy của một nút và tổng entropy có trọng số (theo số lượng ví dụ) của các nút con. Độ đo entropy của một nút là độ đo entropy của các ví dụ trong nút đó.
Ví dụ: hãy xem xét các giá trị entropy sau:
- entropy của nút mẹ = 0,6
- entropy của một nút con có 16 ví dụ liên quan = 0,2
- entropy của một nút con khác với 24 ví dụ có liên quan = 0,1
Vì vậy, 40% ví dụ nằm trong một nút con và 60% nằm trong nút con còn lại. Vì thế:
- tổng entropy có trọng số của các nút con = (0,4 * 0,2) + (0,6 * 0,1) = 0,14
Vậy mức tăng thông tin là:
- mức tăng thông tin = entropy của nút mẹ – tổng entropy có trọng số của các nút con
- mức tăng thông tin = 0,6 – 0,14 = 0,46
Hầu hết bộ phân tách đều tìm cách tạo ra các điều kiện giúp tối đa hoá mức tăng thông tin.
điều kiện trong bộ
Trong cây quyết định, điều kiện kiểm tra sự hiện diện của một mục trong một tập hợp các mục. Ví dụ: sau đây là một điều kiện trong tập hợp:
house-style in [tudor, colonial, cape]
Trong quá trình suy luận, nếu giá trị của đặc điểm về phong cách của ngôi nhà là tudor hoặc colonial hoặc cape, thì điều kiện này sẽ đánh giá là Có. Nếu giá trị của thuộc tính phong cách riêng là một giá trị khác (ví dụ: ranch), thì điều kiện này sẽ đánh giá là Không.
Các điều kiện trong tập hợp thường tạo ra cây quyết định hiệu quả hơn so với các điều kiện kiểm thử các đặc điểm được mã hoá một lần nóng.
L
lá
Mọi điểm cuối trong cây quyết định. Không giống như điều kiện, một nút lá không thực hiện kiểm thử. Thay vào đó, một nút lá là một dự đoán có thể xảy ra. Lá cũng là nút cuối của một đường dẫn suy luận.
Ví dụ: cây quyết định sau đây có 3 nút lá:
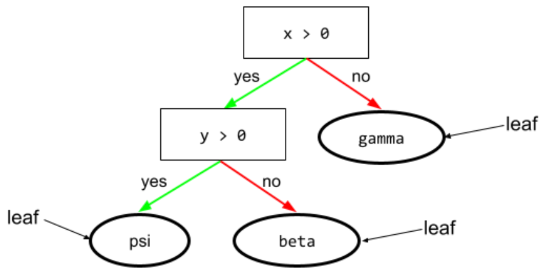
Hãy xem Cây quyết định trong khoá học Rừng quyết định để biết thêm thông tin.
Không
nút (cây quyết định)
Trong cây quyết định, bất kỳ điều kiện hoặc nút lá nào.
Hãy xem Cây quyết định trong khoá học Rừng quyết định để biết thêm thông tin.
điều kiện phi nhị phân
Một điều kiện chứa nhiều hơn 2 kết quả có thể xảy ra. Ví dụ: điều kiện không phải nhị phân sau đây có 3 kết quả có thể xảy ra:
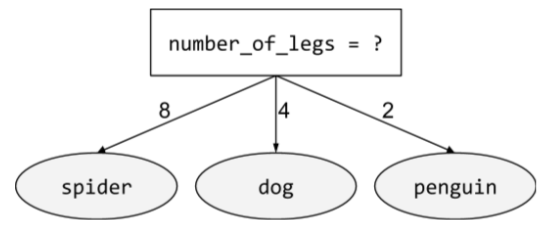
Hãy xem Các loại điều kiện trong khoá học Rừng quyết định để biết thêm thông tin.
O
điều kiện xiên
Trong cây quyết định, điều kiện liên quan đến nhiều đặc điểm. Ví dụ: nếu chiều cao và chiều rộng đều là các đặc điểm, thì sau đây là điều kiện xiên:
height > width
Tương phản với điều kiện căn chỉnh theo trục.
Hãy xem Các loại điều kiện trong khoá học Rừng quyết định để biết thêm thông tin.
đánh giá ngoài túi (đánh giá OOB)
Một cơ chế để đánh giá chất lượng của rừng quyết định bằng cách kiểm thử từng cây quyết định dựa trên các ví dụ không được dùng trong quá trình huấn luyện cây quyết định đó. Ví dụ: trong biểu đồ sau, hãy lưu ý rằng hệ thống huấn luyện từng cây quyết định trên khoảng 2/3 số ví dụ, sau đó đánh giá dựa trên 1/3 số ví dụ còn lại.
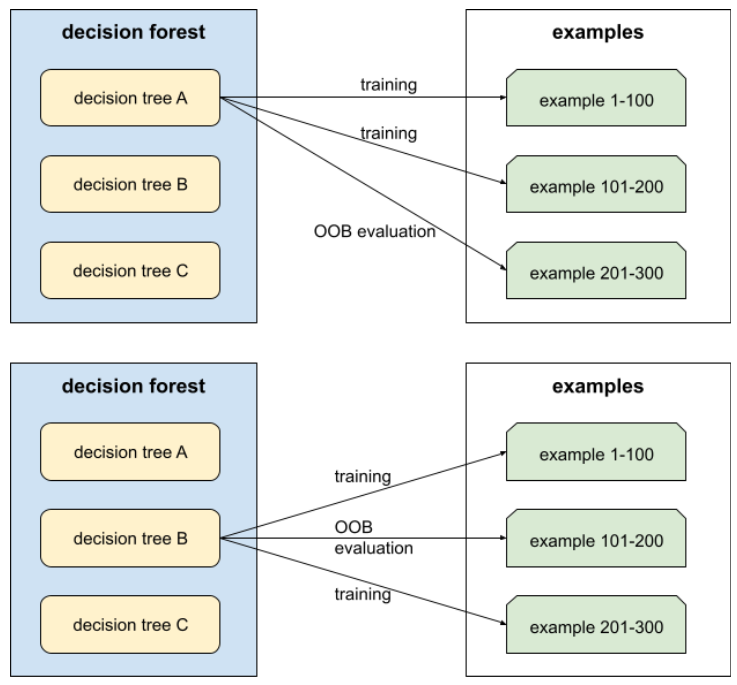
Đánh giá ngoài mẫu là một phương pháp tính toán hiệu quả và thận trọng để ước tính cơ chế xác thực chéo. Trong quy trình xác thực chéo, một mô hình sẽ được huấn luyện cho mỗi vòng xác thực chéo (ví dụ: 10 mô hình được huấn luyện trong quy trình xác thực chéo 10 lần). Với hoạt động đánh giá OOB, một mô hình duy nhất sẽ được huấn luyện. Vì phương pháp lấy mẫu lại giữ lại một số dữ liệu của mỗi cây trong quá trình huấn luyện, nên việc đánh giá OOB có thể sử dụng dữ liệu đó để ước tính phương pháp xác thực chéo.
Hãy xem phần Đánh giá ngoài túi trong khoá học Rừng quyết định để biết thêm thông tin.
Điểm
mức độ quan trọng của biến hoán vị
Một loại mức độ quan trọng của biến đánh giá mức tăng lỗi dự đoán của một mô hình sau khi hoán vị các giá trị của đối tượng. Mức độ quan trọng của biến hoán vị là một chỉ số độc lập với mô hình.
Điểm
rừng ngẫu nhiên
Một tập hợp gồm cây quyết định trong đó mỗi cây quyết định được huấn luyện bằng một nhiễu ngẫu nhiên cụ thể, chẳng hạn như phương pháp lấy mẫu lại.
Rừng ngẫu nhiên là một loại rừng quyết định.
Hãy xem Rừng ngẫu nhiên trong khoá học Rừng quyết định để biết thêm thông tin.
gốc
Nút bắt đầu (điều kiện đầu tiên) trong cây quyết định. Theo quy ước, sơ đồ đặt gốc ở đầu cây quyết định. Ví dụ:
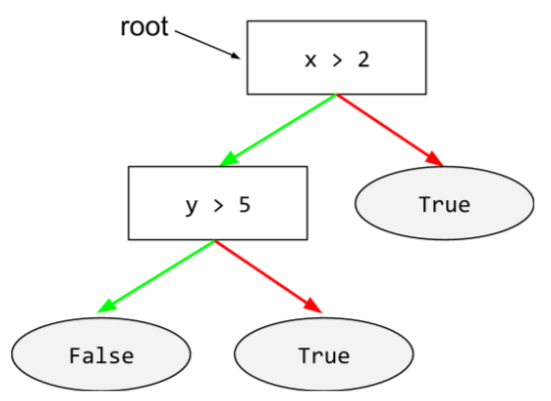
S
lấy mẫu có hoàn lại
Một phương pháp chọn các mục trong một tập hợp các mục đề xuất, trong đó bạn có thể chọn cùng một mục nhiều lần. Cụm từ "có thay thế" có nghĩa là sau mỗi lần chọn, mục đã chọn sẽ được trả về nhóm các mục đề xuất. Phương pháp ngược lại, lấy mẫu không thay thế, có nghĩa là một mục đề xuất chỉ có thể được chọn một lần.
Ví dụ: hãy xem xét tập hợp trái cây sau:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Giả sử hệ thống chọn ngẫu nhiên fig làm mục đầu tiên.
Nếu sử dụng phương pháp lấy mẫu có thay thế, thì hệ thống sẽ chọn mục thứ hai trong tập hợp sau:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Có, đó là cùng một tập hợp như trước đây, vì vậy, hệ thống có thể chọn lại fig.
Nếu sử dụng phương pháp lấy mẫu không thay thế, thì sau khi được chọn, mẫu không thể được chọn lại. Ví dụ: nếu hệ thống chọn ngẫu nhiên fig làm mẫu đầu tiên, thì fig không thể được chọn lại. Do đó, hệ thống sẽ chọn mẫu thứ hai trong tập hợp sau (đã giảm):
fruit = {kiwi, apple, pear, cherry, lime, mango}sự co rút
Một siêu tham số trong tăng cường độ dốc giúp kiểm soát việc khớp quá mức. Mức độ giảm trong phương pháp tăng cường độ dốc tương tự như tốc độ học trong phương pháp giảm độ dốc. Độ co rút là một giá trị thập phân trong khoảng từ 0,0 đến 1,0. Giá trị co rút thấp sẽ giảm tình trạng khớp quá mức nhiều hơn giá trị co rút lớn.
tách
Trong cây quyết định, một tên khác cho điều kiện.
bộ chia
Trong khi huấn luyện một cây quyết định, quy trình (và thuật toán) chịu trách nhiệm tìm ra điều kiện tốt nhất tại mỗi nút.
T
thử nghiệm
Trong cây quyết định, một tên khác cho điều kiện.
ngưỡng (đối với cây quyết định)
Trong điều kiện căn chỉnh theo trục, giá trị mà đối tượng đang được so sánh. Ví dụ: 75 là giá trị ngưỡng trong điều kiện sau:
grade >= 75
Hãy xem phần Bộ chia chính xác để phân loại nhị phân bằng các đặc điểm số trong khoá học Rừng quyết định để biết thêm thông tin.
V
mức độ quan trọng của biến
Một tập hợp các điểm số cho biết tầm quan trọng tương đối của từng đặc điểm đối với mô hình.
Ví dụ: hãy xem xét một cây quyết định ước tính giá nhà. Giả sử cây quyết định này sử dụng 3 đặc điểm: kích thước, độ tuổi và kiểu dáng. Nếu một tập hợp các mức độ quan trọng của biến cho 3 đặc điểm được tính là {size=5.8, age=2.5, style=4.7}, thì kích thước quan trọng hơn đối với cây quyết định so với độ tuổi hoặc kiểu dáng.
Có nhiều chỉ số về tầm quan trọng của biến, có thể cung cấp thông tin cho các chuyên gia về học máy về nhiều khía cạnh của mô hình.
W
trí tuệ tập thể
Ý tưởng cho rằng việc lấy ý kiến hoặc ước tính trung bình của một nhóm lớn người ("đám đông") thường mang lại kết quả tốt một cách đáng ngạc nhiên. Ví dụ: hãy xem xét một trò chơi mà mọi người đoán số lượng kẹo thạch được đóng gói trong một chiếc bình lớn. Mặc dù hầu hết các dự đoán riêng lẻ đều không chính xác, nhưng trung bình của tất cả các dự đoán đã được chứng minh bằng thực nghiệm là gần với số lượng thực tế của kẹo thạch trong bình một cách đáng ngạc nhiên.
Tập hợp là một phần mềm tương tự như trí tuệ tập thể. Ngay cả khi các mô hình riêng lẻ đưa ra dự đoán không chính xác, việc tính trung bình các dự đoán của nhiều mô hình thường tạo ra những dự đoán tốt một cách đáng ngạc nhiên. Ví dụ: mặc dù cây quyết định riêng lẻ có thể đưa ra dự đoán kém chính xác, nhưng rừng quyết định thường đưa ra dự đoán rất chính xác.