1. Before you begin
In this codelab, you'll learn the basic "Hello, World" of ML, where instead of programming explicit rules in a language, such as Java or C++, you'll build a system trained on data to infer the rules that determine a relationship between numbers.
Consider the following problem: You're building a system that performs activity recognition for fitness tracking. You might have access to the speed at which a person is walking and attempt to infer their activity based on that speed using a conditional.

if(speed<4){
status=WALKING;
}
You could extend that to running with another condition.

if(speed<4){
status=WALKING;
} else {
status=RUNNING;
}
In a final condition, you could similarly detect cycling.

if(speed<4){
status=WALKING;
} else if(speed<12){
status=RUNNING;
} else {
status=BIKING;
}
Now, consider what happens when you want to include an activity, like golf. It's less obvious how to create a rule to determine the activity.

// Now what?
It's extremely difficult to write a program that will recognize the golfing activity, so what do you do? You can use ML to solve the problem!
Prerequisites
Before attempting this codelab, you'll want to have:
- A solid knowledge of Python
- Basic programming skills
What you'll learn
- The basics of machine learning
What you'll build
- Your first machine learning model
What you'll need
If you've never created an ML model using TensorFlow, you can use Colaboratory, a browser-based environment containing all the required dependencies. You can find the code for the rest of the codelab running in Colab.
If you're using a different IDE, make sure you have Python installed. You'll also need TensorFlow and the NumPy library. You can learn more about and install TensorFlow here. Install NumPy here.
2. What is ML?
Consider the traditional manner of building apps, as represented in the following diagram:

You express rules in a programming language. They act on data and your program provides answers**.** In the case of the activity detection, the rules (the code you wrote to define activity types) acted upon the data (the person's movement speed) to produce an answer: the return value from the function for determining the activity status of the user (whether they were walking, running, biking, or doing something else).
The process for detecting that activity status via ML is very similar, only the axes are different.

Instead of trying to define the rules and express them in a programming language, you provide the answers (typically called labels) along with the data, and the machine infers the rules that determine the relationship between the answers and data. For example, your activity detection scenario might look like this in an ML context:
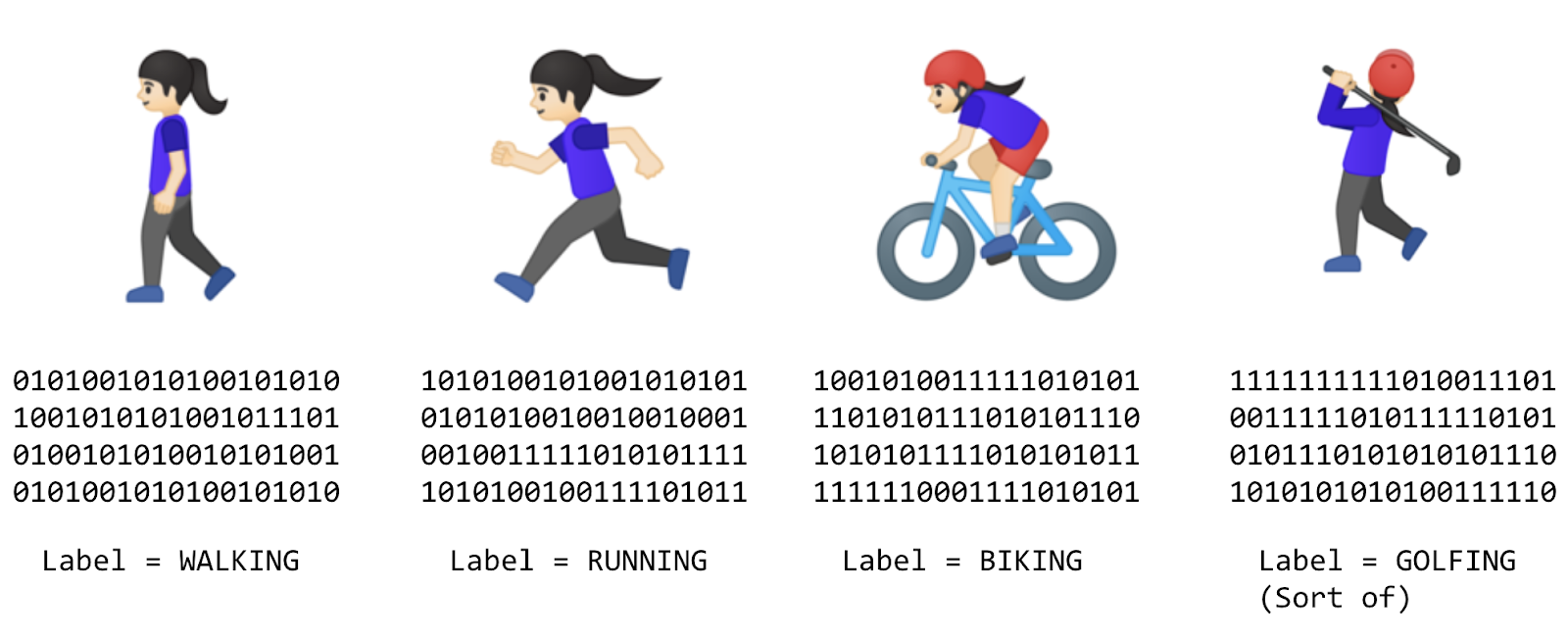
You gather lots of data and label it to effectively say, "This is what walking looks like," or "This is what running looks like." Then, the computer can infer the rules that determine, from the data, what the distinct patterns that denote a particular activity are.
Beyond being an alternative method to programming that scenario, that approach also gives you the ability to open new scenarios, such as the golfing one that may not have been possible under the rules-based traditional programming approach.
In traditional programming, your code compiles into a binary that is typically called a program. In ML, the item that you create from the data and labels is called a model.
So, if you go back to this diagram:

Consider the result of that to be a model, which is used like this at runtime:

You pass the model some data and the model uses the rules that it inferred from the training to make a prediction, such as, "That data looks like walking," or "That data looks like biking."
3. Create your first ML model
Consider the following sets of numbers. Can you see the relationship between them?
X: | -1 | 0 | 1 | 2 | 3 | 4 |
Y: | -2 | 1 | 4 | 7 | 10 | 13 |
As you look at them, you might notice that the value of X is increasing by 1 as you read left to right and the corresponding value of Y is increasing by 3. You probably think that Y equals 3X plus or minus something. Then, you'd probably look at the 0 on X and see that Y is 1, and you'd come up with the relationship Y=3X+1.
That's almost exactly how you would use code to train a model to spot the patterns in the data!
Now, look at the code to do it.
How would you train a neural network to do the equivalent task? Using data! By feeding it with a set of X's and a set of Y's, it should be able to figure out the relationship between them.
Imports
Start with your imports. Here, you're importing TensorFlow and calling it tf for ease of use.
Next, import a library called numpy, which represents your data as lists easily and quickly.
The framework for defining a neural network as a set of sequential layers is called keras, so import that, too.
import tensorflow as tf
import numpy as np
from tensorflow import keras
Define and compile the neural network
Next, create the simplest possible neural network. It has one layer, that layer has one neuron, and the input shape to it is only one value.
model = tf.keras.Sequential([keras.layers.Dense(units=1, input_shape=[1])])
Next, write the code to compile your neural network. When you do so, you need to specify two functions—a loss and an optimizer.
In this example, you know that the relationship between the numbers is Y=3X+1.
When the computer is trying to learn that, it makes a guess, maybe Y=10X+10. The loss function measures the guessed answers against the known correct answers and measures how well or badly it did.
Next, the model uses the optimizer function to make another guess. Based on the loss function's result, it tries to minimize the loss. At this point, maybe it will come up with something like Y=5X+5. While that's still pretty bad, it's closer to the correct result (the loss is lower).
The model repeats that for the number of epochs, which you'll see shortly.
First, here's how to tell it to use mean_squared_error for the loss and stochastic gradient descent (sgd) for the optimizer. You don't need to understand the math for those yet, but you can see that they work!
Over time, you'll learn the different and appropriate loss and optimizer functions for different scenarios.
model.compile(optimizer='sgd', loss='mean_squared_error')
Provide the data
Next, feed some data. In this case, you take the six X and six Y variables from earlier. You can see that the relationship between those is that Y=3X+1, so where X is -1, Y is -2.
A python library called NumPy provides lots of array type data structures to do this. Specify the values as an array in NumPy with np.array[].
xs = np.array([-1.0, 0.0, 1.0, 2.0, 3.0, 4.0], dtype=float)
ys = np.array([-2.0, 1.0, 4.0, 7.0, 10.0, 13.0], dtype=float)
Now you have all the code you need to define the neural network. The next step is to train it to see if it can infer the patterns between those numbers and use them to create a model.
4. Train the neural network
The process of training the neural network, where it learns the relationship between the X's and Y's, is in the model.fit call. That's where it will go through the loop before making a guess, measuring how good or bad it is (the loss), or using the optimizer to make another guess. It will do that for the number of epochs that you specify. When you run that code, you'll see the loss will be printed out for each epoch.
model.fit(xs, ys, epochs=500)
For example, you can see that for the first few epochs, the loss value is quite large, but it's getting smaller with each step.

As the training progresses, the loss soon gets very small.

By the time the training is done, the loss is extremely small, showing that our model is doing a great job of inferring the relationship between the numbers.

You probably don't need all 500 epochs and can experiment with different amounts. As you can see from the example, the loss is really small after only 50 epochs, so that might be enough!
5. Use the model
You have a model that has been trained to learn the relationship between X and Y. You can use the model.predict method to have it figure out the Y for a previously unknown X. For example, if X is 10, what do you think Y will be? Take a guess before you run the following code:
print(model.predict([10.0]))
You might have thought 31, but it ended up being a little over. Why do you think that is?
Neural networks deal with probabilities, so it calculated that there is a very high probability that the relationship between X and Y is Y=3X+1, but it can't know for sure with only six data points. The result is very close to 31, but not necessarily 31.
As you work with neural networks, you'll see that pattern recurring. You will almost always deal with probabilities, not certainties, and will do a little bit of coding to figure out what the result is based on the probabilities, particularly when it comes to classification.
6. Congratulations
Believe it or not, you covered most of the concepts in ML that you'll use in far more complex scenarios. You learned how to train a neural network to spot the relationship between two sets of numbers by defining the network. You defined a set of layers (in this case only one) that contained neurons (also in this case, only one), which you then compiled with a loss function and an optimizer.
The collection of a network, loss function, and optimizer handles the process of guessing the relationship between the numbers, measuring how well they did, and then generating new parameters for new guesses. Learn more at TensorFlow.org.
Learn more
To learn about how ML and TensorFlow can help with your computer vision models, proceed to Build a computer vision model with TensorFlow.
