이 페이지는 Cloud Translation API를 통해 번역되었습니다.

분석 트랩

'모든 모델이 잘못되었지만, 일부 모델은 쓸모가 있다.' — 조지 박스, 1978년

통계 기법은 강력하지만 한계가 있습니다. 이러한 제한사항을 이해하면 BF 스키너가 셰익스피어가 무작위로 예측되는 것보다 더 많이 운율을 사용하지 않았다고 주장한 것과 같은 실수와 부정확한 주장을 피하는 데 도움이 될 수 있습니다. (스키너의 연구는 통계적 신뢰도가 낮았습니다.¹)

불확실성 및 오류 막대

분석에서 불확실성을 지정하는 것이 중요합니다. 다른 사람의 분석에서 불확실성을 수치화하는 것도 똑같이 중요합니다. 그래프에 추세를 표시하는 것처럼 보이지만 오류 막대가 겹치는 데이터 포인트는 패턴을 전혀 나타내지 않을 수 있습니다. 또한 특정 연구나 통계 테스트에서 유용한 결론을 도출하기에는 불확실성이 너무 클 수 있습니다. 연구에 필지가 포함된 수준의 정확성이 필요한 경우 불확실성이 +/- 500m인 지리 공간 데이터 세트는 불확실성이 너무 커서 사용할 수 없습니다.

또는 불확실성 수준은 의사결정 과정에서 유용할 수 있습니다. 결과에 대한 불확실성이 20% 인 특정 수처리를 뒷받침하는 데이터가 있으면 불확실성을 해결하기 위해 프로그램을 지속적으로 모니터링하면서 해당 수처리를 구현하는 것이 좋습니다.

확률적 신경망은 단일 값 대신 값의 분포를 예측하여 불확실성을 수치화할 수 있습니다.

혼동

교란 변수, 혼동 또는 공분모는 연구 대상이 아닌 변수로,연구 대상 변수에 영향을 미치고 결과를 왜곡할 수 있습니다. 예를 들어 공중 보건 정책 특성을 기반으로 입력 국가의 사망률을 예측하는 ML 모델을 생각해 보겠습니다. 중위 연령이 기능이 아니라고 가정해 보겠습니다. 또한 일부 국가의 인구는 다른 국가보다 고령인 것으로 가정해 보겠습니다. 이 모델은 중위 연령이라는 혼동 변수를 무시하므로 잘못된 사망률을 예측할 수 있습니다.

미국에서는 인종이 사망률 데이터에 기록되지만 계급이 아닌 인종만 사망률 데이터에 기록되며, 인종은 사회경제적 계급과 밀접한 관련이 있습니다. 의료, 영양, 위험한 직업, 안전한 주택에 대한 접근성과 같은 계급 관련 혼동 요소는 인종보다 사망률에 더 큰 영향을 미칠 수 있지만 데이터 세트에 포함되지 않아 무시될 수 있습니다.³ 이러한 혼동 요소를 파악하고 통제하는 것은 유용한 모델을 구축하고 의미 있고 정확한 결론을 도출하는 데 매우 중요합니다.

인종은 포함하고 계급은 포함하지 않는 기존 사망률 데이터를 바탕으로 모델을 학습하면 계급이 사망률을 더 잘 예측하는 경우에도 인종을 기반으로 사망률을 예측할 수 있습니다. 이로 인해 인과 관계에 대한 부정확한 가정과 환자 사망률에 대한 부정확한 예측이 발생할 수 있습니다. ML 실무자는 데이터에 혼동 요소가 있는지, 그리고 데이터 세트에서 어떤 의미 있는 변수가 누락되었는지 확인해야 합니다.

1985년 하버드 의대와 하버드 보건대학의 관찰 코호트 연구인 간호사 건강 연구에서 에스트로겐 대체 요법을 받는 코호트 구성원의 심장마비 발생률이 에스트로겐을 복용하지 않은 코호트 구성원보다 낮은 것으로 나타났습니다. 그 결과, 의사들은 2002년 임상 연구에서 장기 에스트로겐 요법으로 인한 건강 위험이 확인될 때까지 수십 년 동안 폐경 및 폐경 후 환자에게 에스트로겐을 처방했습니다. 폐경 후 여성에게 에스트로겐을 처방하는 관행은 중단되었지만, 그 전에 수만 명의 조기 사망을 초래했습니다.

여러 혼동 요소가 이러한 연관성을 일으켰을 수 있습니다. 역학자들은 호르몬 대체 요법을 받는 여성이 그렇지 않은 여성에 비해 더 날씬하고, 더 높은 학력과 더 높은 소득을 보유하며, 건강에 더 관심이 많고, 운동할 가능성이 더 높다는 사실을 발견했습니다. 여러 연구에서 교육과 부유함이 심장병 위험을 줄이는 것으로 나타났습니다. 이러한 효과는 에스트로겐 요법과 심장마비 간의 명백한 상관관계를 혼동시켰을 것입니다.⁴

음수 비율

음수가 포함된 경우⁵ 비율을 사용하지 마세요. 모든 종류의 의미 있는 이익과 손실이 가려질 수 있습니다. 간단한 계산을 위해 레스토랑 업계에 200만 개의 일자리가 있다고 가정해 보겠습니다. 2020년 3월 말에 100만 개의 일자리가 사라지고 10개월 동안 순 변화가 없으며 2021년 2월 초에 90만 개의 일자리가 다시 생겨난다면 2021년 3월 초에 전년 대비 비교하면 음식점 일자리가 5% 만 감소한 것으로 보일 것입니다. 다른 변동사항이 없다고 가정하면 2021년 4월 말의 전년 대비 비교는 음식점 일자리가 90% 증가했다고 제안할 수 있으며, 이는 현실과는 매우 다른 그림입니다.

적절하게 표준화된 실제 숫자를 사용하는 것이 좋습니다. 자세한 내용은 숫자 데이터 작업을 참고하세요.

사후 편향 및 사용할 수 없는 상관관계

인과 관계 오류는 이벤트 A 뒤에 이벤트 B가 발생했으므로 이벤트 A가 이벤트 B를 일으켰다는 가정입니다. 더 간단히 말해, 인과 관계가 존재하지 않는 곳에 인과 관계가 있다고 가정하는 것입니다. 더 간단히 말하자면 상관관계가 인과관계를 증명하지는 않습니다.

명확한 원인과 결과 관계 외에도 다음과 같은 이유로 상관관계가 발생할 수 있습니다.

순수한 우연 (메인주 이혼율과 마가린 소비량 간의 강한 상관관계를 비롯한 예시는 타일러 비겐의 허위 상관관계 참고).
두 변수 간의 실제 관계이지만 어떤 변수가 원인이고 어떤 변수가 영향을 받는지는 명확하지 않습니다.
상관된 변수가 서로 관련이 없더라도 두 변수에 모두 영향을 미치는 세 번째 별도의 원인입니다. 예를 들어 전 세계 인플레이션으로 인해 요트와 셀러리의 가격이 모두 오를 수 있습니다.⁶

기존 데이터를 넘어선 상관성을 추정하는 것도 위험합니다. Huff는 비가 약간 내리면 작물이 좋아지지만 비가 너무 많이 내리면 작물이 손상된다고 지적합니다. 비와 작물 결과 간의 관계는 비선형입니다.⁷ (비선형 관계에 관한 자세한 내용은 다음 두 섹션을 참고하세요.) 존스는 전쟁과 기근과 같이 예측할 수 없는 사건이 많아 시계열 데이터의 향후 예측에 엄청난 불확실성이 적용된다고 지적합니다.⁸

또한 원인과 결과에 기반한 진정한 상관관계도 의사 결정에 도움이 되지 않을 수 있습니다. �프는 1950년대의 결혼 가능성과 대학 교육 간의 상관 관계를 예로 들었습니다. 대학에 다닌 여성은 결혼할 가능성이 낮았지만, 대학에 다닌 여성이 애초에 결혼할 생각이 적었을 수도 있습니다. 이 경우 대학 교육은 결혼 가능성을 변화시키지 않았습니다.⁹

분석에서 데이터 세트의 두 변수 간에 상관관계를 감지하면 다음을 묻습니다.

어떤 종류의 상관관계인가요? 원인과 결과, 가짜, 알 수 없는 관계, 제3 변수로 인한 것인가요?
데이터에서 추론하는 것이 얼마나 위험한가요? 학습 데이터 세트에 없는 데이터에 대한 모든 모델 예측은 사실상 데이터에서 보간 또는 외삽된 것입니다.
상관관계를 사용하여 유용한 결정을 내릴 수 있나요? 예를 들어 낙관은 임금 인상과 상관성이 높을 수 있지만 특정 국가의 사용자가 작성한 소셜 미디어 게시물과 같은 대규모 텍스트 데이터 자료의 감정 분석은 해당 국가의 임금 인상을 예측하는 데 유용하지 않습니다.

ML 전문가는 모델을 학습할 때 일반적으로 라벨과 강하게 상관관계가 있는 특성을 찾습니다. 특성과 라벨 간의 관계를 잘 이해하지 못하면 가짜 상관관계에 기반한 모델, 과거 동향이 실제로는 지속되지 않는데도 향후에도 지속될 것이라고 가정하는 모델 등 이 섹션에 설명된 문제가 발생할 수 있습니다.

선형 편향

'비선형 세상에서의 선형 사고'에서 바트 드 랑헤, 스테파노 푼토니, 리처드 라릭은 선형 편향을 많은 현상이 비선형임에도 불구하고 인간의 뇌가 선형 관계를 기대하고 찾는 경향이라고 설명합니다. 예를 들어 인간의 태도와 행동 간의 관계는 선이 아니라 볼록한 곡선입니다. 드 랑헤 외 연구원이 인용한 2007년 Journal of Consumer Policy 논문에서 Jenny van Doorn 등은 설문조사 응답자의 환경에 대한 우려와 응답자의 유기농 제품 구매 간의 관계를 모델링했습니다. 환경에 대한 우려가 가장 큰 사람들은 유기농 제품을 더 많이 구매했지만 다른 모든 응답자 간에 차이는 거의 없었습니다.

유기농 제품 구매와 환경 문제 점수의 비교. 오른쪽 끝에 급격한 볼록 곡선이 있는 대부분 평평한 선이 표시됨 — van Doorn 등 논문에서 간소화 및 조정된 유기농 구매와 환경 문제 점수의 그래프

모델이나 연구를 설계할 때는 비선형 관계의 가능성을 고려하세요. A/B 테스트에서는 비선형 관계를 놓칠 수 있으므로 세 번째 중간 조건인 C도 테스트해 보세요. 또한 선형으로 보이는 초기 동작이 계속 선형인지 또는 향후 데이터에서 더 많은 대수나 기타 비선형 동작이 표시될 수 있는지 고려하세요.

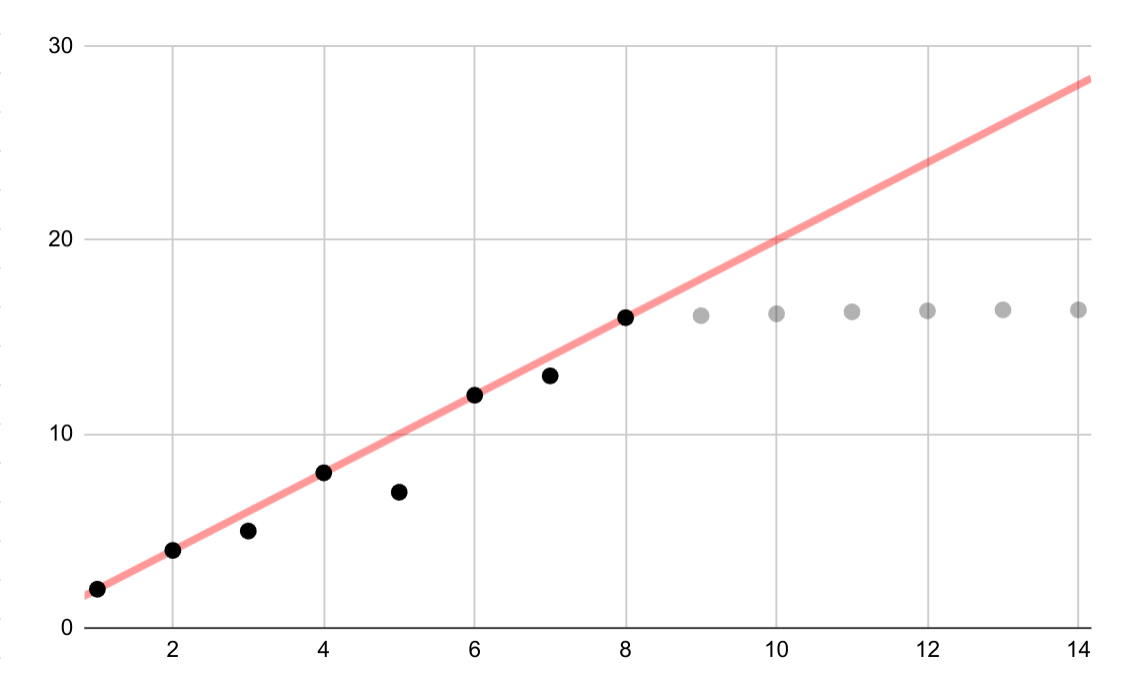
데이터의 전반부에 잘 맞고 그 이후에는 점점 더 잘 맞지 않는 것을 보여주는 대수 데이터의 선형 적합입니다. — 로그 데이터에 적합하지 않은 선형 근사 예

이 가상 예에서는 대수 데이터에 대한 잘못된 선형 적합을 보여줍니다. 처음 몇 개의 데이터 포인트만 사용할 수 있는 경우 변수 간에 지속적인 선형 관계가 있다고 가정하는 것은 유혹적이지만 잘못된 방법입니다.

선형 보간 유형

보간은 가상의 포인트를 도입하고 실제 측정 간의 간격에 의미 있는 변동이 포함될 수 있으므로 데이터 포인트 간의 보간을 검사합니다. 예를 들어 선형 보간으로 연결된 4개의 데이터 포인트의 다음 시각화를 고려해 보겠습니다.

직선으로 연결된 4개의 점을 보여주는 시간 경과에 따른 진폭 — 선형 보간 예시

그런 다음 선형 보간으로 삭제되는 데이터 포인트 사이의 변동 예시를 살펴보겠습니다.

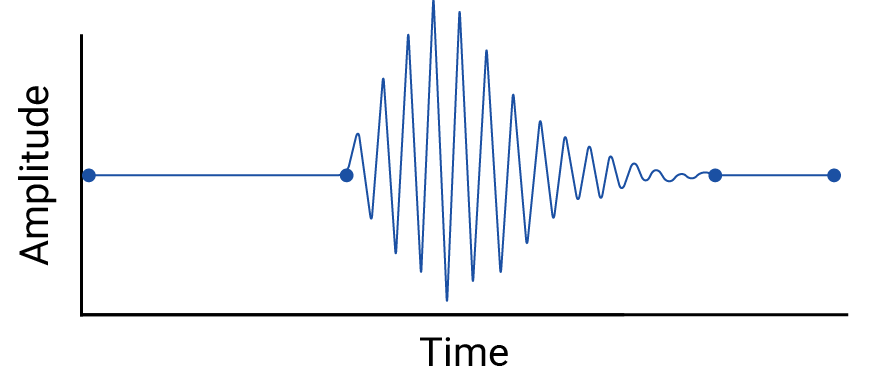
이전과 동일한 점이지만 두 번째와 세 번째 지점 간에 큰 변동이 있습니다. — 데이터 포인트 간의 유의미한 변동 (지진)의 예

이 예시는 지진계가 연속 데이터를 수집하므로 이 지진을 놓치지 않을 것이라는 점을 고려하여 고안되었습니다. 하지만 보간으로 가정된 가정과 데이터 전문가가 놓칠 수 있는 실제 현상을 보여주는 데는 유용합니다.

룽게 현상

'다항식 흔들림'이라고도 하는 룽게 현상은 선형 보간법 및 선형 편향과는 반대의 스펙트럼에 있는 문제입니다. 데이터에 다항식 보간을 맞출 때 너무 높은 차수(다항식 방정식에서 가장 높은 지수인 차수 또는 순서)의 다항식을 사용할 수 있습니다. 이렇게 하면 가장자리에서 이상한 발진이 발생합니다. 예를 들어 다항식 방정식의 최고차 항이 $x^{11}$인 11차 다항식 보간을 대략 선형 데이터에 적용하면 데이터 범위의 시작과 끝에서 상당히 나쁜 예측이 발생합니다.

11도 다항식 보간으로 적합된 대략 선형 데이터로, 처음 두 데이터 포인트 간에 급격한 상승 스파이크가 있고 마지막 두 데이터 포인트 간에 급격한 하락 스파이크가 있습니다. — 다항식 흔들기의 예

ML 컨텍스트에서 유사한 현상은 오버피팅입니다.

통계적 감지 실패

통계 테스트가 너무 약해서 작은 효과를 감지하지 못하는 경우도 있습니다. 통계 분석의 검정력이 낮으면 실제 이벤트를 올바르게 식별할 가능성이 낮아 거짓음성 가능성이 높습니다. 캐서린 버튼 외 연구원들은 Nature에 다음과 같이 적었습니다. '특정 분야의 연구가 20%의 검정력으로 설계되었다면, 해당 분야에서 발견할 수 있는 실제 비무효 효과가 100개 있다면 이 연구에서는 그중 20개만 발견할 것으로 예상됩니다.' 샘플 크기를 늘리거나 신중하게 연구 설계를 하면 도움이 될 수 있습니다.

ML에서 유사한 상황은 분류 문제와 분류 임곗값 선택입니다. 임곗값을 높게 선택하면 거짓양성이 줄고 거짓음성이 늘어나며, 임곗값을 낮게 선택하면 거짓양성이 늘어나고 거짓음성이 줄어듭니다.

상관관계는 선형 관계를 감지하도록 설계되었으므로 통계적 유효성 문제 외에도 변수 간의 비선형 상관관계가 누락될 수 있습니다. 마찬가지로 변수가 서로 관련이 있지만 통계적으로 상관관계가 없을 수도 있습니다. 변수가 음의 상관관계가 있지만 전혀 관련이 없는 경우도 있습니다. 이를 버크슨의 역설 또는 버크슨의 오류라고 합니다. 베크슨의 오류의 전형적인 예는 일반 인구와 비교하여 병원 입원 환자 집단을 볼 때 위험 요인과 심각한 질병 간에 발생하는 허위의 음의 상관관계입니다. 이 상관관계는 선택 과정(병원 입원이 필요한 심각한 질환)에서 발생합니다.

다음 중 해당하는 상황이 있는지 고려하세요.

오래된 모델 및 잘못된 가정

동작 (그리고 세상)이 변할 수 있으므로 좋은 모델도 시간이 지남에 따라 성능이 저하될 수 있습니다. Netflix의 초기 예측 모델은 고객층이 젊고 기술에 능숙한 사용자에서 일반인으로 바뀌면서 지원 중단되었습니다.¹⁰

모델에는 2008년 시장 폭락과 같이 모델의 심각한 장애가 발생할 때까지 숨겨져 있을 수 있는 묵시적이고 부정확한 가정이 포함될 수도 있습니다. 금융 업계의 VaR (Value at Risk) 모델은 모든 트레이더의 포트폴리오에 대한 최대 손실을 정확하게 추정한다고 주장했습니다. 예를 들어 99% 의 경우 최대 손실이 10만달러라고 예상했습니다. 그러나 비정상적인 비정상 종료 조건에서는 예상 최대 손실이 $100,000인 포트폴리오가 $1,000,000 이상 손실되는 경우가 있었습니다.

VaR 모델은 다음과 같은 잘못된 가정을 기반으로 했습니다.

과거 시장 변화는 향후 시장 변화를 예측하는 데 도움이 됩니다.
예측된 수익의 기반이 되는 분포는 정규 (가늘고 예측 가능한) 분포였습니다.

가우스 분포와 유사한 k=5의 폰 미제스 분포와 더 평평한 k=1 및 k=.2 — von Mises 분포의 그래프입니다. K가 클 때는 꼬리가 가늘고 K가 작을 때는 꼬리가 굵습니다.

실제로는 기본 분포가 뚱뚱한 꼬리, '야생' 또는 프랙탈이었습니다. 즉, 정규 분포에서 예측하는 것보다 드물게 발생하는 극단적인 장기적 사건이 발생할 위험이 훨씬 더 높았습니다. 실제 분포의 뚱뚱한 꼬리 특성은 잘 알려져 있었지만 이에 따른 조치는 취해지지 않았습니다. 자동 판매가 포함된 컴퓨터 기반 거래 등 다양한 현상이 얼마나 복잡하고 밀접하게 결합되어 있는지는 잘 알려지지 않았습니다.¹¹

집계 문제

집계된 데이터(대부분의 인구통계 및 역학 데이터 포함)에는 특정 함정이 적용됩니다. 심슨의 역설 또는 통합 역설은 혼동 요인과 오해된 인과 관계로 인해 데이터가 다른 수준에서 집계될 때 명백한 추세가 사라지거나 반전되는 집계된 데이터에서 발생합니다.

생태학적 오류는 한 집계 수준의 인구에 관한 정보를 다른 집계 수준으로 잘못 추정하는 것으로, 이 경우 주장이 유효하지 않을 수 있습니다. 한 지역의 농업 노동자 중 40% 가 앓고 있는 질병이 더 많은 인구에서는 동일한 유병률을 보이지 않을 수 있습니다. 또한 해당 지역에는 이 질병의 유행이 이와 비슷하게 높지 않은 격리된 농장이나 농업 마을이 있을 가능성이 매우 높습니다. 영향을 덜 받는 지역에서도 40% 의 유병률을 가정하는 것은 잘못된 추론입니다.

수정 가능한 지역 단위 문제 (MAUP)는 1984년 CATMOG 38에서 샘 오픈쇼가 설명한 지리 정보 데이터의 잘 알려진 문제입니다. 지리정보 데이터 전문가는 데이터를 집계하는 데 사용되는 영역의 모양과 크기에 따라 데이터의 변수 간에 거의 모든 상관관계를 설정할 수 있습니다. 특정 정당에 유리하도록 선거구를 그리는 것이 MAUP의 한 예입니다.

이러한 모든 상황은 한 집계 수준에서 다른 집계 수준으로 부적절하게 추론하는 것을 포함합니다. 분석 수준에 따라 집계가 다르거나 완전히 다른 데이터 세트가 필요할 수 있습니다.¹²

인구 조사, 인구통계, 역학 데이터는 일반적으로 개인 정보 보호를 위해 구역별로 집계되며 이러한 구역은 의미 있는 실제 경계를 기반으로 하지 않는 임의의 구역인 경우가 많습니다. 이러한 유형의 데이터를 사용할 때 ML 전문가는 선택한 영역의 크기와 모양 또는 집계 수준에 따라 모델 성능과 예측이 달라지는지, 그리고 달라지는 경우 모델 예측이 이러한 집계 문제 중 하나의 영향을 받는지 확인해야 합니다.

참조

버튼, 캐서린 외. '전원 장애: 샘플 크기가 작으면 신경과학의 신뢰성이 떨어지는 이유' Nature Reviews Neuroscience vol 14 (2013), 365–376. DOI: https://doi.org/10.1038/nrn3475

카이로, 알베르토님. 차트가 거짓말하는 방법: 시각적 정보에 대해 더 스마트하게 알아보기 뉴욕: W.W. Norton, 2019.

데이븐포트, 토마스 H. '예측 분석 입문' 관리자를 위한 데이터 분석 기초에 관한 HBR 가이드 (보스턴: HBR Press, 2018) 81~86쪽

드 랑헤, 바트, 스테파노 푼토니, 리처드 라리크 '비선형 세상에서의 선형적 사고' HBR Guide to Data Analytics Basics for Managers (보스턴: HBR Press, 2018) 131~154쪽

엘렌버그, 조던 How Not to Be Wrong: The Power of Mathematical Thinking 뉴욕: 펭귄, 2014년.

핼프, 대럴 통계를 사용하여 거짓말하는 방법 뉴욕: W.W. Norton, 1954.

존스, 벤 데이터 문제 방지 Hoboken, NJ: Wiley, 2020.

오픈쇼우, 스탠. 'The Modifiable Areal Unit Problem'(조정 가능한 지역 단위 문제), CATMOG 38(노리치, 영국: Geo Books 1984) 37.

금융 모델링의 위험: VaR 및 경제 붕괴, 제111차 의회 (2009년) (Nassim N. Taleb, Richard Bookstaber)의 연구에 따르면

리터, 데이비드 '상관관계에 따라 조치를 취해야 하는 경우와 취해서는 안 되는 경우' HBR Guide to Data Analytics Basics for Managers (보스턴: HBR Press, 2018) 103~109쪽

툴치킨스키, 시어도어 H. 및 엘레나 A. Varavikova. The New Public Health, 3rd ed. San Diego: Academic Press, 2014, pp 91-147의 '3장: 인구의 건강 측정, 모니터링, 평가' DOI: https://doi.org/10.1016/B978-0-12-415766-8.00003-3.

반 도른, 제니, 피터 C. Verhoef, Tammo H. A. Bijmolt '정책 연구에서 태도와 행동 간의 비선형 관계의 중요성' Journal of Consumer Policy 30 (2007) 75–90. DOI: https://doi.org/10.1007/s10603-007-9028-3

이미지 참조

'Von Mises Distribution'을(를) 기반으로 합니다. Rainald62, 2018. 소스

Ellenberg 125. ↩
Huff 77~79. �프는 프린스턴의 여론 조사 기관을 언급했지만 덴버 대학교의 국가 여론 조사 센터가 작성한 1944년 4월 보고서를 생각하고 있었을 수 있습니다. ↩
Tulchinsky 및 Varavikova. ↩
게리 타우베스, 뉴욕 타임스 매거진,2007년 9월 16일, 건강에 좋은 음식을 정말로 알고 있나요? ↩
엘렌버그 78. ↩
Huff 91-92. ↩
Huff 93. ↩
Jones 157~167. ↩
Huff 95. ↩
데이븐포트 84. ↩
Nassim N.의 의회 증언을 참고하세요. Taleb and Richard Bookstaber, The Risks of Financial Modeling: VaR and the Economic Meltdown, 111th Congress (2009) 11-67. ↩
카이로 155, 162 ↩

생각하는 함정

시각화 트랩

분석 트랩 컬렉션을 사용해 정리하기 내 환경설정을 기준으로 콘텐츠를 저장하고 분류하세요.