本詞彙表定義了人工智慧術語。
A
消融
評估特徵或元件重要性的技術,方法是暫時從模型中移除該特徵或元件。接著,您會重新訓練模型,但不使用該特徵或元件。如果重新訓練的模型成效明顯變差,則表示移除的特徵或元件可能很重要。
舉例來說,假設您使用 10 項特徵訓練分類模型,並在測試集中達到 88% 的準確率。如要檢查第一個特徵的重要性,可以只使用其他九個特徵重新訓練模型。如果重新訓練的模型成效大幅下降 (例如精確度低於 55%),表示移除的特徵可能很重要。反之,如果重新訓練的模型成效一樣良好,則該特徵可能不是那麼重要。
消融法也有助於判斷下列項目的重要性:
- 較大的元件,例如較大型機器學習系統的整個子系統
- 程序或技術,例如資料預先處理步驟
在這兩種情況下,您都會觀察到移除元件後,系統的效能變化 (或沒有變化)。
A/B 測試
這是一種統計方法,可比較兩種 (或更多) 技術,也就是 A 和 B。一般來說,A 是現有技術,B 則是新技術。A/B 測試不僅能判斷哪種技術成效較佳,還能判斷差異是否具有統計顯著性。
A/B 測試通常會比較兩種技術的單一指標,例如比較兩種技術的模型準確度。不過,A/B 測試也可以比較任何有限數量的指標。
加速器晶片
這類專用硬體元件專門執行深度學習演算法所需的關鍵運算。
與一般用途 CPU 相比,加速器晶片 (簡稱加速器) 可大幅提升訓練和推論工作的速度和效率。非常適合訓練神經網路和類似的運算密集型工作。
加速器晶片的例子包括:
- Google 的 Tensor Processing Unit (TPU),具備專用硬體,可進行深度學習。
- NVIDIA 的 GPU 最初是為圖形處理而設計,但可啟用平行處理,大幅提升處理速度。
精確度
正確分類預測次數除以預測總次數。也就是:
舉例來說,如果模型做出 40 項正確預測和 10 項錯誤預測,準確率為:
二元分類會為正確預測和不正確預測的不同類別提供特定名稱。因此,二元分類的準確度公式如下:
其中:
詳情請參閱機器學習速成課程中的「分類:準確度、喚回率、精確度和相關指標」。
動作
在強化學習中,代理會透過環境的狀態轉換機制,代理會使用政策選擇動作。
啟動函式
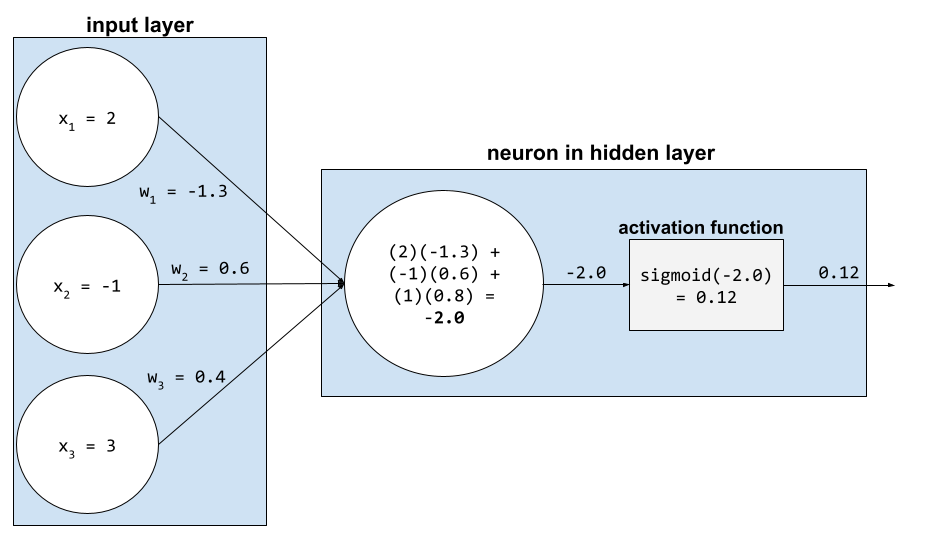
這項函式可讓類神經網路學習特徵與標籤之間的非線性 (複雜) 關係。
熱門的啟用函式包括:
啟動函式的圖形絕不會是單一直線。 舉例來說,ReLU 啟動函式的繪圖包含兩條直線:

Sigmoid 啟動函式的繪圖如下所示:

詳情請參閱機器學習速成課程中的「類神經網路:啟動函式」。
主動學習
訓練方法,演算法會選擇部分資料進行學習。當標籤範例稀少或取得成本高昂時,主動學習就特別有價值。主動學習演算法不會盲目尋找各種加上標籤的範例,而是會選擇性地尋找學習所需的特定範圍範例。
AdaGrad
這項精密的梯度下降演算法會重新調整每個參數的梯度,有效為每個參數提供獨立的學習率。如要查看完整說明,請參閱「Adaptive Subgradient Methods for Online Learning and Stochastic Optimization」。
改編
與微調或微調同義。
代理程式
這類軟體可以根據多模態使用者輸入內容進行推論,以便代表使用者規劃及執行動作。
在強化學習中,代理程式是使用政策的實體,可盡量提高從環境狀態轉換中獲得的預期報酬。
聽命行事
代理的形容詞形式。代理式是指代理程式擁有的特質 (例如自主性)。
代理工作流程
代理程式會自主規劃及執行動作,以達成目標。這個過程可能涉及推理、叫用外部工具,以及自行修正計畫。
凝聚式分群
請參閱階層式分群。
AI slop
生成式 AI 系統的輸出內容,品質不佳但數量龐大。舉例來說,如果網頁充斥著 AI 濫用內容,就會出現大量低品質的 AI 生成內容,且製作成本低廉。
異常偵測
找出離群值的程序。舉例來說,如果特定特徵的平均值為 100,標準差為 10,則異常偵測功能應將值 200 標示為可疑。
AR
擴增實境的縮寫。
PR 曲線下面積
請參閱「PR AUC (PR 曲線下的面積)」。
ROC 曲線下面積
請參閱 AUC (ROC 曲線下面積)。
通用人工智慧
展現廣泛解決問題、創意和適應能力的人類以外機制。舉例來說,展現人工通用智慧的程式可以翻譯文字、創作交響樂,以及擅長玩尚未發明的遊戲。
人工智慧
可解決複雜任務的非人類程式或模型。 舉例來說,翻譯文字的程式或模型,以及從放射線圖像識別疾病的程式或模型,都展現了人工智慧。
從正式角度來看,機器學習是人工智慧的子領域。不過,近年來有些機構開始交替使用「人工智慧」和「機器學習」這兩個詞彙。
注意力
類神經網路中使用的機制,可指出特定字詞或字詞一部分的重要性。注意力機制會壓縮模型預測下一個符記/字詞所需資訊的量。典型的注意力機制可能包含一組輸入內容的加權總和,其中每個輸入內容的權重是由類神經網路的另一部分計算而得。
另請參閱自注意力和多頭自注意力,這些是 Transformer 的建構區塊。
如要進一步瞭解自我注意力機制,請參閱機器學習速成課程中的「LLM:什麼是大型語言模型?」一文。
屬性
特徵 的同義詞。
在機器學習公平性中,屬性通常是指與個人相關的特徵。
屬性取樣
訓練決策樹系的策略,其中每個決策樹在學習條件時,只會考慮可能的特徵隨機子集。一般來說,每個節點會取樣不同的功能子集。反之,如果訓練決策樹時沒有屬性取樣,系統會考慮每個節點的所有可能特徵。
AUC (ROC 曲線下面積)
介於 0.0 和 1.0 之間的數字,代表二元分類模型區分正類和負類的能力。AUC 越接近 1.0,代表模型區分各類別的能力越好。
舉例來說,下圖顯示分類模型完美區分正類 (綠色橢圓) 和負類 (紫色矩形)。這個不切實際的完美模型 AUC 值為 1.0:

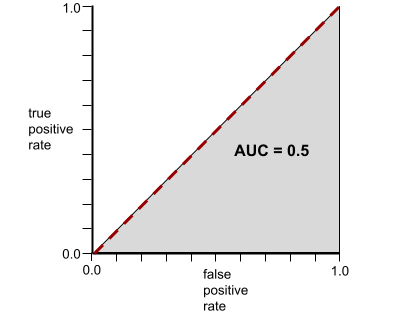
反之,下圖顯示分類模型產生隨機結果時的結果。這個模型的 AUC 為 0.5:

是,前一個模型的 AUC 為 0.5,而非 0.0。
大多數模型都介於這兩個極端之間。舉例來說,下列模型會將正向和負向結果分開,因此 AUC 值介於 0.5 和 1.0 之間:

AUC 會忽略您為分類閾值設定的任何值。AUC 則會考量所有可能的分類門檻。
詳情請參閱機器學習速成課程中的「分類:ROC 和 AUC」。
擴增實境
這項技術會在使用者看到的實景上疊加電腦生成的圖像,提供合成影像。
自動編碼器
這類系統會學習從輸入內容中擷取最重要的資訊。自動編碼器是由編碼器和解碼器組合而成。自動編碼器會依下列兩步驟程序運作:
- 編碼器會將輸入內容對應至 (通常) 有損的低維度 (中繼) 格式。
- 解碼器會將低維度格式對應至原始高維度輸入格式,藉此建構原始輸入的有損版本。
自動編碼器會經過端對端訓練,讓解碼器盡可能從編碼器的中繼格式重建原始輸入內容。由於中間格式比原始格式小 (維度較低),自動編碼器會被迫學習輸入內容中的重要資訊,因此輸出內容不會與輸入內容完全相同。
例如:
- 如果輸入資料是圖像,非精確副本會與原始圖像相似,但經過些許修改。非完全相同的副本可能會移除原始圖像的雜訊,或填補一些遺失的像素。
- 如果輸入資料是文字,自動編碼器會產生模仿原始文字的新文字 (但不會完全相同)。
另請參閱變分自動編碼器。
自動評估
使用軟體判斷模型輸出內容的品質。
如果模型輸出內容相對簡單,指令碼或程式可以將模型輸出內容與黃金回應進行比較。這類自動評估有時也稱為「程式輔助評估」。ROUGE 或 BLEU 等指標通常有助於程式輔助評估。
如果模型輸出內容複雜或沒有正確答案,有時會由稱為「自動評分器」的獨立機器學習程式執行自動評估。
與人工評估形成對比。
自動化偏誤
當決策人員偏好自動決策系統提出的建議,而非未經自動化處理的資訊,即使自動決策系統出錯也一樣。
詳情請參閱機器學習速成課程的「公平性:偏見類型」一文。
AutoML
任何用於建構機器學習 模型的自動化程序。AutoML 可自動執行下列工作:
AutoML 可節省數據資料學家開發機器學習管道的時間和精力,並提高預測準確度,因此對他們來說非常實用。這項工具也能幫助非專業人士,讓他們更容易完成複雜的機器學習工作。
詳情請參閱機器學習密集課程的「自動化機器學習 (AutoML)」。
autorater evaluation
用來判斷生成式 AI 模型輸出內容品質的混合機制,結合了人工評估和自動評估。自動評分員是根據人工評估產生的資料訓練而成的機器學習模型。理想情況下,自動評估員會學習模仿人類評估員。您可以使用預先建構的自動評估者,但最好是針對評估工作微調自動評估者。
自我迴歸模型
模型:根據先前的預測結果推斷預測結果。舉例來說,自動迴歸語言模型會根據先前預測的權杖,預測下一個權杖。所有以 Transformer 為基礎的大型語言模型都是自動迴歸模型。
相較之下,GAN 型圖像模型通常不是自動迴歸模型,因為這類模型會在單一前向傳遞中生成圖像,而不是逐步疊代。不過,某些圖像生成模型是自動迴歸模型,因為這類模型會分階段生成圖像。
輔助損失
損失函式:與類神經網路 模型的主要損失函式搭配使用,有助於在權重隨機初始化的早期疊代期間,加快訓練速度。
輔助損失函式會將有效梯度推送到先前的層。這有助於在訓練期間促進收斂,進而解決梯度消失問題。
k 的平均精確度
這項指標會彙整模型在單一提示中的成效,並產生排序結果,例如書籍建議的編號清單。k 的平均精確度,就是每個相關結果的 k 值精確度平均值。因此,k 的平均精確度公式為:
\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]
其中:
- \(n\) 是清單中相關項目的數量。
與 k 處的回想形成對比。
軸對齊條件
在決策樹中,條件只涉及單一特徵。舉例來說,如果 area 是某項功能,則下列為軸對齊條件:
area > 200
與斜線條件形成對比。
B
反向傳播
訓練類神經網路需要多次疊代,才能完成下列雙階段週期:
- 在正向傳遞期間,系統會處理批次的範例,產生預測結果。系統會將每個預測結果與每個標籤值進行比較。預測值與標籤值之間的差異,就是該範例的損失。系統會匯總所有範例的損失,計算目前批次的總損失。
- 在反向傳播期間,系統會調整所有隱藏層中所有神經元的權重,以減少損失。
類神經網路通常包含許多隱藏層,每個隱藏層都有許多神經元。每個神經元都會以不同方式造成整體損失。 反向傳播會判斷是否要增加或減少套用至特定神經元的權重。
學習率是控制每個反向傳遞增加或減少各權重程度的乘數。相較於較小的學習率,較大的學習率會使每個權重增加或減少更多。
以微積分來說,反向傳播會實作微積分的連鎖法則。也就是說,反向傳播會計算相對於每項參數的誤差偏導數。
多年前,機器學習從業人員必須編寫程式碼,才能實作反向傳播。Keras 等現代機器學習 API 現在會為您實作反向傳播。呼!
詳情請參閱機器學習速成課程中的類神經網路。
裝袋
這是一種訓練集合的方法,其中每個組成模型都會訓練隨機子集的訓練範例,並取樣替換。舉例來說,隨機森林是透過裝袋法訓練的決策樹集合。
「bagging」一詞是「bootstrap aggregating」的縮寫。
詳情請參閱「決策樹林」課程中的隨機森林。
詞袋
不論順序為何,都代表詞組或段落中的字詞。舉例來說,詞袋模型會以相同方式表示下列三個詞組:
- 狗跳躍
- 跳躍的小狗
- 狗跳過
每個字詞都會對應到稀疏向量中的索引,而向量會為詞彙表中的每個字詞建立索引。舉例來說,詞組「the dog jumps」會對應至特徵向量,且與「the」、「dog」和「jumps」這三個字詞對應的索引值不為零。非零值可以是下列任一值:
- 1:表示字詞存在。
- 字詞在袋子中出現的次數。舉例來說,如果片語是「the maroon dog is a dog with maroon fur」,則「maroon」和「dog」都會以 2 表示,其他字詞則以 1 表示。
- 其他值,例如字詞出現在包包中的次數的對數。
基準
模型,用來做為比較其他模型 (通常是較複雜的模型) 效能的參考點。舉例來說,邏輯迴歸模型可做為深層模型的良好基準。
針對特定問題,基準可協助模型開發人員量化新模型必須達成的最低預期成效,才能發揮效用。
基礎模型
Batch
單一訓練疊代中使用的一組範例。批次大小會決定批次中的樣本數量。
如要瞭解批次與週期之間的關係,請參閱週期。
詳情請參閱機器學習速成課程中的「線性迴歸:超參數」。
批次推論
對分成較小子集 (「批次」) 的多個未標記範例進行推論預測的程序。
批次推論可運用加速器晶片的平行處理功能。也就是說,多個加速器可以同時對不同批次的未標籤範例推斷預測結果,大幅增加每秒的推斷次數。
詳情請參閱機器學習速成課程中的「正式版機器學習系統:靜態與動態推論」。
批次正規化
正規化啟動函式在隱藏層的輸入或輸出。批次正規化可提供下列優點:
批次大小
批次中的樣本數量。 舉例來說,如果批次大小為 100,模型就會在每次疊代時處理 100 個範例。
以下是常見的批次大小策略:
- 隨機梯度下降 (SGD),批次大小為 1。
- 完整批次:批次大小是整個訓練集中的範例數。舉例來說,如果訓練集包含一百萬個範例,則批次大小為一百萬個範例。完整批次通常是效率不彰的策略。
- 微批次,批次大小通常介於 10 到 1000 之間。迷你批次通常是最有效率的策略。
詳情請參閱下列說明文章:
貝氏類神經網路
可考量權重和輸出內容不確定性的機率性類神經網路。標準類神經網路迴歸模型通常會預測純量值;舉例來說,標準模型預測的房價為 853,000 美元。相較之下,貝氏類神經網路會預測值的分布情形;舉例來說,貝氏模型預測的房價為 853,000 元,標準差為 67,200 元。
貝葉斯類神經網路會依據 貝氏定理 計算權重和預測的不確定性。如果量化不確定性很重要,例如在與藥物相關的模型中,貝氏神經網路就很有用。貝氏類神經網路也有助於避免過度擬合。
貝式最佳化
機率迴歸模型是一種技術,可透過貝葉斯學習技術量化不確定性,進而最佳化計算成本高昂的目標函式。由於貝氏最佳化本身非常昂貴,因此通常用於最佳化評估成本高昂且參數數量較少的作業,例如選取超參數。
貝爾曼方程式
在強化學習中,最佳 Q 函式會滿足下列身分:
\[Q(s, a) = r(s, a) + \gamma \mathbb{E}_{s'|s,a} \max_{a'} Q(s', a')\]
強化學習演算法會套用這個身分,使用下列更新規則建立 Q-learning:
\[Q(s,a) \gets Q(s,a) + \alpha \left[r(s,a) + \gamma \displaystyle\max_{\substack{a_1}} Q(s',a') - Q(s,a) \right] \]
除了強化學習,貝爾曼方程式也適用於動態規劃。請參閱 維基百科的貝爾曼方程式條目。
BERT (基於 Transformer 的雙向編碼器表示技術)
文字表示法的模型架構。訓練完成的 BERT 模型可做為大型模型的一部分,用於文字分類或其他機器學習工作。
BERT 具有下列特徵:
- 使用 Transformer 架構,因此依賴自注意力。
- 使用 Transformer 的編碼器部分。編碼器的工作是產生優質的文字表示法,而不是執行分類等特定工作。
- 是否為雙向。
- 使用遮罩進行非監督式訓練。
BERT 的變體包括:
如要瞭解 BERT 的總覽,請參閱「Open Sourcing BERT: State-of-the-Art Pre-training for Natural Language Processing」。
偏誤 (倫理/公平性)
1. 對某些事物、人或族群抱有刻板印象、偏見或偏袒心態。這些偏見可能會影響資料的收集和解讀、系統設計,以及使用者與系統的互動方式。這類偏誤的形式包括:
2. 取樣或通報程序造成的系統性錯誤。這類偏誤的形式包括:
詳情請參閱機器學習速成課程的「公平性:偏見類型」一文。
偏誤 (數學) 或偏誤項
從原點開始的截距或偏移量。偏誤是機器學習模型中的參數,以以下任一符號表示:
- b
- w0
舉例來說,在下列公式中,偏差值是 b:
在簡單的二維線中,偏差值只代表「y 截距」。舉例來說,下圖中線條的偏差值為 2。
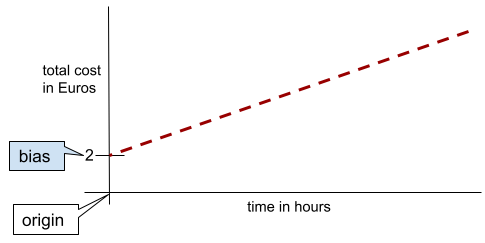
並非所有模型都從原點 (0,0) 開始,因此會產生偏差。舉例來說,假設遊樂園的入場費為 2 歐元,顧客每多待一小時就要額外支付 0.5 歐元。因此,對應總成本的模型有 2 歐元的偏差,因為最低成本為 2 歐元。
請勿將偏誤與倫理和公平性方面的偏誤或預測偏誤混淆。
詳情請參閱機器學習速成課程中的「線性迴歸」。
雙向
這個詞彙用來描述系統,該系統會評估目標文字區段「之前」和「之後」的文字。相反地,單向系統只會評估目標文字區段之前的文字。
舉例來說,假設遮罩語言模型必須判斷下列問題中底線代表的字詞機率:
你怎麼了?
單向語言模型只能根據「What」、「is」和「the」這幾個字詞提供的背景資訊,計算機率。相較之下,雙向語言模型也能從「with」和「you」取得脈絡,這可能有助於模型產生更準確的預測。
雙向語言模型
語言模型:根據前後文字,判斷特定詞元出現在文字片段特定位置的機率。
bigram
二元語法,其中 N=2。
二元分類
這類分類工作會預測兩個互斥類別之一:
舉例來說,下列兩個機器學習模型都會執行二元分類:
- 判斷電子郵件是否為垃圾郵件 (正類) 或非垃圾郵件 (負類) 的模型。
- 評估醫療症狀,判斷某人是否罹患特定疾病 (正向類別),或未罹患該疾病 (負向類別)。
與多元分類形成對比。
詳情請參閱機器學習密集課程的分類。
二元條件
在決策樹中,條件只有兩種可能的結果,通常是「是」或「否」。舉例來說,以下是二元條件:
temperature >= 100
與非二元條件形成對比。
詳情請參閱「決策樹林」課程中的「條件類型」。
特徵分塊
bucketing 的同義詞。
黑盒模型
模型的「推理」過程難以理解或無法理解。也就是說,雖然人類可以瞭解提示如何影響回覆,但無法確切判斷黑箱模型如何決定回覆內容。換句話說,黑箱模型缺少可解釋性。
BLEU (雙語評估研究)
評估機器翻譯的指標,介於 0.0 和 1.0 之間,例如從西班牙文翻譯成日文。
為計算分數,BLEU 通常會比較機器學習模型的翻譯 (生成的文字) 與人類專家的翻譯 (參考文字)。生成文字和參考文字中 N 元語法的相符程度,決定了 BLEU 分數。
這項指標的原始論文是「BLEU:一種自動評估機器翻譯的方法」。
另請參閱 BLEURT。
BLEURT (基於 Transformer 的雙語評估研究)
評估機器翻譯品質的指標,特別是英譯中和中譯英。
在英譯中和中譯英方面,BLEURT 比 BLEU 更貼近人類評分。與 BLEU 不同,BLEURT 強調語意 (意義) 相似性,並可容納改寫。
BLEURT 採用預先訓練的大型語言模型 (確切來說是 BERT),然後以人工翻譯的文字微調模型。
這項指標的原始論文是「BLEURT:Learning Robust Metrics for Text Generation」。
增強
這項機器學習技術會反覆將一組簡單且不甚準確的分類模型 (稱為「弱分類器」) 組合為高準確度的分類模型 (稱為「強分類器」),方法是提高模型目前分類錯誤的範例權重。
詳情請參閱決策樹林課程中的梯度提升決策樹?。
定界框
在圖片中,感興趣區域周圍矩形的 (x, y) 座標,例如下圖中的狗。

廣播
在矩陣數學運算中,將運算元的形狀擴展為與該運算相容的維度。舉例來說,線性代數規定矩陣加法運算中的兩個運算元必須具有相同維度。因此,您無法將形狀為 (m, n) 的矩陣加到長度為 n 的向量。廣播會將長度為 n 的向量虛擬擴展為形狀 (m, n) 的矩陣,並在每個資料欄中複製相同的值,藉此啟用這項作業。
詳情請參閱以下有關 NumPy 廣播的說明。
資料分組
將單一特徵轉換為多個二進位特徵,稱為「值區」或「分組」,通常是根據值範圍。切碎的特徵通常是連續特徵。
舉例來說,您可以將溫度範圍切分成離散值區,例如:
- 攝氏 10 度以下為「寒冷」類別。
- 攝氏 11 到 24 度則屬於「溫和」類別。
- 攝氏 25 度以上則為「溫暖」類別。
模型會將同一值區中的每個值視為相同。舉例來說,13 和 22 的值都在溫和值區中,因此模型會將這兩個值視為相同。
詳情請參閱機器學習速成課程中的「數值資料:分箱」。
C
校準層
預測後調整項,通常用於考量預測偏差。調整後的預測結果和機率應與觀察到的標籤集分配情形相符。
候選人生成
由推薦系統選取的初始建議組合。舉例來說,假設書店提供 10 萬種書籍,候選項目生成階段會為特定使用者建立較小的合適書籍清單,例如 500 本。但即使是 500 本,對使用者來說也太多了。建議系統後續的階段 (例如評分和重新排序) 成本較高,會將這 500 項建議縮減為更實用的一小部分。
詳情請參閱「推薦系統」課程中的候選項目生成總覽。
候選抽樣
這項訓練期間最佳化功能會計算所有正向標籤的機率 (例如使用 softmax),但只會針對隨機抽樣的負向標籤進行計算。舉例來說,如果範例標示為「米格魯」和「狗」,候選項目取樣會計算下列項目的預測機率和對應的損失項:
- beagle
- dog
- 其餘負類別的隨機子集 (例如「貓」、「棒棒糖」、「圍籬」)。
這個概念是,只要正向類別一律獲得適當的正向強化,負向類別就能從較不頻繁的負向強化中學習,而這確實是根據經驗觀察到的現象。
與計算所有負面類別預測結果的訓練演算法相比,候選項目取樣的運算效率更高,尤其是在負面類別數量非常龐大時。
類別資料
特徵具有一組特定可能值。舉例來說,假設有名為 traffic-light-state 的類別特徵,只能有下列三種可能值之一:
redyellowgreen
將 traffic-light-state 視為類別特徵,模型就能瞭解 red、green 和 yellow 對駕駛人行為的不同影響。
與數值型資料形成對比。
詳情請參閱機器學習速成課程的「處理類別資料」。
因果語言模型
單向語言模型的同義詞。
如要比較語言模型中不同的方向性方法,請參閱雙向語言模型。
質心
叢集的中心,由 k-means 或 k-median 演算法決定。舉例來說,如果 k 為 3,則 k-means 或 k-median 演算法會找出 3 個群集中心。
詳情請參閱分群課程中的「分群演算法」。
以群集中心為準的分群
這類分群演算法會將資料整理成非階層式叢集。k-means 是最常用的以質心為基礎的分群演算法。
與階層式叢集演算法形成對比。
詳情請參閱分群課程中的「分群演算法」。
思維鏈提示
這項提示工程技術會引導大型語言模型 (LLM) 逐步說明推論過程。舉例來說,請看以下提示,並特別注意第二句:
如果車輛在 7 秒內從時速 0 英里加速到時速 60 英里,駕駛人會感受到多少 G 力?請在答案中列出所有相關計算。
LLM 的回覆可能:
- 顯示一連串物理公式,並在適當位置代入 0、60 和 7 。
- 說明選擇這些公式的原因,以及各種變數的意義。
思維鏈提示會強制 LLM 執行所有計算,因此可能得出更正確的答案。此外,使用者還能透過連鎖思考提示檢查 LLM 的步驟,判斷答案是否合理。
字元 N 元語法 F 分數 (ChrF)
評估機器翻譯模型的指標。字元 N 元語法 F 分數會判斷參考文字中的 N 元語法與 ML 模型生成文字中的 N 元語法重疊程度。
字元 N 元語法 F 分數與 ROUGE 和 BLEU 系列的指標類似,但有以下例外情況:
- 字元 N 元語法 F 分數會針對字元 N 元語法運算。
- ROUGE 和 BLEU 會對字詞 N-gram 或符記執行運算。
對話
與機器學習系統 (通常是大型語言模型) 一來一往的對話內容。對話中的先前互動 (您輸入的內容和大型語言模型的回覆) 會成為後續對話的脈絡。
聊天機器人是大型語言模型的應用程式。
檢查站
資料會擷取模型參數的狀態,無論是在訓練期間或訓練完成後都適用。舉例來說,在訓練期間,您可以:
- 停止訓練,可能是刻意停止,也可能是因為發生特定錯誤。
- 擷取檢查點。
- 稍後,重新載入檢查點,可能是在不同的硬體上。
- 重新展開訓練。
類別
標籤所屬的類別。 例如:
分類模型會預測類別。相較之下,迴歸模型會預測數字,而非類別。
詳情請參閱機器學習密集課程的分類。
類別平衡資料集
包含類別 標籤的資料集,其中每個類別的例項數量大致相等。舉例來說,假設有一個植物資料集,其二元標籤可以是「原生植物」或「非原生植物」:
- 如果資料集包含 515 種原生植物和 485 種非原生植物,就是類別平衡資料集。
- 如果資料集包含 875 種原生植物和 125 種非原生植物,就是類別不平衡的資料集。
類別平衡資料集和類別不平衡資料集之間沒有正式的分界線。只有在以高度類別不平衡資料集訓練的模型無法收斂時,區別這兩者才顯得重要。詳情請參閱機器學習速成課程中的「資料集:不平衡的資料集」。
分類模型
- 模型會預測輸入句子所用的語言 (法文?西班牙文? 義大利文?)。
- 預測樹種的模型 (是楓樹嗎?Oak?猴麵包樹?
- 模型會預測特定醫療狀況的正類或負類。
相較之下,迴歸模型會預測數字,而非類別。
常見的分類模型有兩種:
分類門檻
在二元分類中,介於 0 到 1 之間的數字會將邏輯迴歸模型的原始輸出內容,轉換為正類別或負類別的預測結果。請注意,分類門檻是由人為選擇的值,而非模型訓練選擇的值。
邏輯迴歸模型會輸出介於 0 和 1 之間的原始值。然後:
- 如果這個原始值大於分類門檻,系統就會預測為正類。
- 如果這個原始值小於分類門檻,系統就會預測為負面類別。
舉例來說,假設分類門檻為 0.8。如果原始值為 0.9,模型就會預測正類。如果原始值為 0.7,模型會預測負類。
詳情請參閱機器學習速成課程中的「門檻和混淆矩陣」。
分類器
分類模型的非正式用語。
不平衡資料集
資料集,其中每個類別的標籤總數差異顯著。舉例來說,假設有一個二元分類資料集,其中兩個標籤的劃分方式如下:
- 1,000,000 個負值長條標籤
- 10 個正值長條標籤
負面與正面標籤的比例為 100,000 比 1,因此這是類別不平衡的資料集。
相較之下,下列資料集是類別平衡,因為負面標籤與正面標籤的比例相對接近 1:
- 517 個負值長條標籤
- 483 個正值長條標籤
多類別資料集也可能出現類別不平衡的情況。舉例來說,下列多元分類資料集也屬於類別不平衡,因為其中一個標籤的範例數量遠多於其他兩個:
- 1,000,000 個標籤,類別為「綠色」
- 200 個標籤,類別為「紫色」
- 350 個標籤,類別為「orange」
訓練不平衡資料集可能會遇到特殊挑戰。詳情請參閱機器學習速成課程中的不平衡的資料集。
剪輯
處理離群值的技巧,包括執行下列任一或兩項操作:
- 將大於最大門檻的特徵值調降至該門檻。
- 將低於最低門檻的特徵值調高至該門檻。
舉例來說,假設特定特徵的值有不到 0.5% 落在 40 到 60 以外的範圍,在這種情況下,您可以採取以下做法:
- 將所有超過 60 (最高門檻) 的值剪輯為 60。
- 將所有低於 40 (最低門檻) 的值剪輯為 40。
離群值可能會損壞模型,有時還會導致訓練期間權重溢位。部分離群值也可能大幅影響準確度等指標。剪除是限制損壞的常見技術。
詳情請參閱機器學習速成課程中的「數值資料:正規化」。
Cloud TPU
專門設計的硬體加速器,用於加快 Google Cloud 上的機器學習工作負載。
分群
將相關範例分組,特別是在非監督式學習期間。所有範例分組完畢後,可選擇由人工為每個叢集提供意義。
目前有許多分群演算法,舉例來說,k-means 演算法會根據範例與群集中心的距離,將範例分群,如下圖所示:

接著,研究人員可以查看這些叢集,並為叢集 1 加上「矮樹」標籤,為叢集 2 加上「全尺寸樹木」標籤。
再舉一例,假設叢集演算法是根據範例與中心點的距離來分群,如下圖所示:

詳情請參閱分群課程。
共同改編
神經元幾乎只依賴特定其他神經元的輸出內容,而非整個網路的行為,藉此預測訓練資料中的模式,這是一種不良行為。如果驗證資料中沒有導致共同適應的模式,共同適應就會導致過度擬合。Dropout 正規化可減少共同適應,因為 dropout 可確保神經元不會只依賴特定其他神經元。
協同過濾
根據其他眾多使用者的興趣,預測某位使用者的興趣。協同過濾方法通常用於推薦系統。
詳情請參閱推薦系統課程中的協同過濾。
精簡型號
任何設計在運算資源有限的小型裝置上執行的模型。舉例來說,精簡模型可以在手機、平板電腦或嵌入式系統上執行。
運算
(名詞) 模型或系統使用的運算資源,例如處理能力、記憶體和儲存空間。
請參閱加速器晶片。
概念偏移
特徵與標籤之間的關係發生變化。 概念漂移會隨著時間降低模型品質。
在訓練期間,模型會學習訓練集中特徵與標籤之間的關係。如果訓練集中的標籤是真實世界的良好替代指標,模型應該就能做出良好的真實世界預測。不過,由於概念漂移,模型的預測結果會隨著時間而準確度下降。
舉例來說,假設有一個二元分類模型,可預測特定車款是否「省油」。也就是說,特徵可以是:
- 車輛重量
- 引擎壓縮
- 傳動類型
而標籤則為下列任一情況:
- 省油
- 燃油效率不佳
不過,「省油車」的概念不斷演變。1994 年標示為「省油」的車款,在 2024 年幾乎肯定會標示為「不省油」。如果模型發生概念漂移,隨著時間推移,預測結果的實用性會越來越低。
與非平穩性比較並對照。
狀況
在決策樹中,執行測試的任何節點。舉例來說,下列決策樹包含兩項條件:
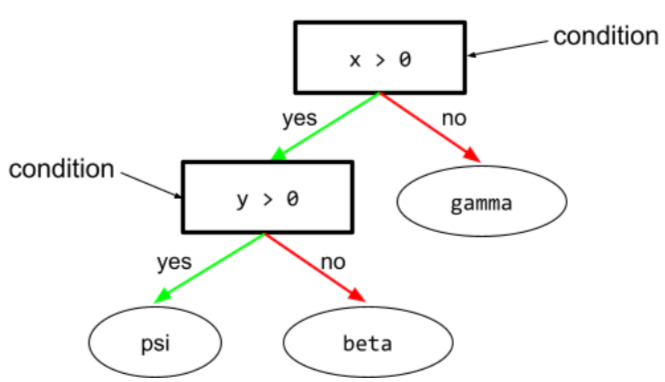
條件也稱為「分割」或「測試」。
對比條件與 leaf。
另請參閱:
詳情請參閱「決策樹林」課程中的「條件類型」。
虛構
幻覺的同義詞。
與「幻覺」相比,「虛構」可能更符合技術上的準確度。 不過,幻覺一詞先流行起來。
設定
指派用於訓練模型的初始屬性值的程序,包括:
在機器學習專案中,您可以透過特殊的設定檔或使用下列設定程式庫進行設定:
確認偏誤
傾向於搜尋、解讀、偏好及回憶資訊,以證實自己原有的信念或假設。機器學習開發人員可能會無意間以影響結果的方式收集或標記資料,進而支持現有的信念。確認偏誤是隱性偏誤的一種形式。
實驗者偏誤是一種確認偏誤,實驗者會持續訓練模型,直到確認先前的假設為止。
混淆矩陣
NxN 表格,彙整分類模型做出的正確和錯誤預測數量。舉例來說,請參考下列二元分類模型的混淆矩陣:
| 腫瘤 (預測) | 非腫瘤 (預測) | |
|---|---|---|
| 腫瘤 (真值) | 18 (TP) | 1 (FN) |
| 非腫瘤 (真值) | 6 (FP) | 452 (TN) |
上述混淆矩陣顯示以下內容:
- 在 19 項基準真相為「腫瘤」的預測中,模型正確分類了 18 項,錯誤分類了 1 項。
- 在 458 項基準真相為「非腫瘤」的預測中,模型正確分類了 452 項,錯誤分類了 6 項。
多類別分類問題的混淆矩陣可協助您找出錯誤模式。舉例來說,假設您有一個 3 類別多類別分類模型,可將三種不同類型的鳶尾花 (Virginica、Versicolor 和 Setosa) 分類,則混淆矩陣如下所示。如果真值是 Virginica,混淆矩陣會顯示模型誤判為 Versicolor 的機率遠高於 Setosa:
| Setosa (預測) | Versicolor (預測) | 維吉尼亞 (預測) | |
|---|---|---|---|
| Setosa (真值) | 88 | 12 | 0 |
| Versicolor (真值) | 6 | 141 | 7 |
| Virginica (真值) | 2 | 27 | 109 |
再舉一例,混淆矩陣可能會顯示,訓練模型辨識手寫數字時,模型傾向於誤判 9 而非 4,或誤判 1 而非 7。
混淆矩陣包含充足資訊,可計算各種成效指標,包括精確度和喚回率。
選區剖析
將句子劃分為較小的文法結構 (「成分」)。機器學習系統的後續部分 (例如自然語言理解模型) 可以比原始句子更輕鬆地剖析組成要素。舉例來說,請參考下列句子:
我朋友認養了兩隻貓。
成分剖析器可將這句話分成以下兩個成分:
- 「我的朋友」是名詞片語。
- 「領養兩隻貓」是動詞片語。
這些構件可以進一步細分為更小的構件。 例如動詞片語
認養了兩隻貓
可再細分為:
- 「採用」是動詞。
- two cats 是另一個名詞片語。
內容比對語言嵌入
嵌入內容,可「理解」字詞和片語,就像流利的人類說話者一樣。脈絡化語言嵌入可理解複雜的語法、語意和脈絡。
舉例來說,假設我們想瞭解英文單字「cow」的嵌入。較舊的嵌入 (例如 word2vec) 可以表示英文字詞,因此嵌入空間中「母牛」與「公牛」之間的距離,會類似於「母羊」與「公羊」或「女性」與「男性」之間的距離。脈絡化語言嵌入則更進一步,可辨識出英語使用者有時會隨意使用「cow」一字,代表母牛或公牛。
脈絡窗口
模型在特定提示中可處理的權杖數量。脈絡窗口越大,模型能使用的資訊就越多,因此能針對提示提供連貫一致的回覆。
連續性特徵
浮點特徵,可能的值範圍無限大,例如溫度或重量。
與離散特徵形成對比。
便利取樣
使用非以科學方式收集的資料集,以便執行快速實驗。之後,請務必改用科學收集的資料集。
收斂
當損失值在每次疊代時幾乎沒有變化或完全沒有變化,即達到此狀態。舉例來說,下列損失曲線顯示大約 700 次疊代後會收斂:
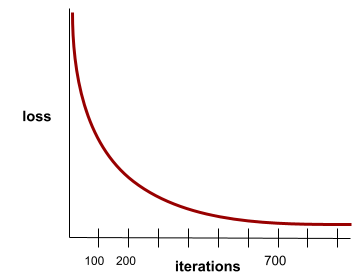
如果額外訓練無法改善模型,模型就會收斂。
在深度學習中,損失值有時會在經過多次疊代後才開始下降,如果長時間出現持續的損失值,您可能會暫時產生錯誤的收斂感。
另請參閱「提早停止」。
詳情請參閱機器學習速成課程中的「模型收斂和損失曲線」。
對話式程式設計
您與生成式 AI 模型之間的疊代式對話,目的是建立軟體。您發出提示,描述某個軟體。接著,模型會根據該說明生成程式碼。接著,您會發出新提示,修正先前提示或生成程式碼中的瑕疵,模型就會生成更新後的程式碼。你們會不斷來回修正,直到生成的軟體夠好為止。
對話式程式開發基本上就是直覺式程式開發的原始意義。
與規格化編碼形成對比。
凸函數
如果函式圖形上方的區域是凸集,則該函式為凸函式。典型的凸函數形狀類似字母 U。舉例來說,下列都是凸函式:
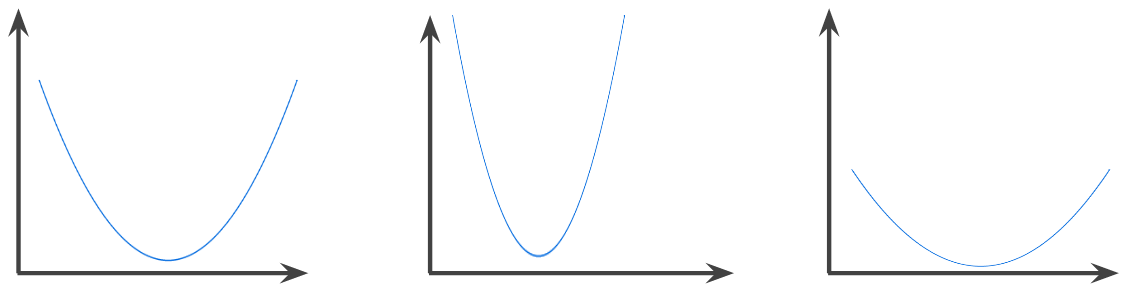
相反地,下列函式並非凸函式。請注意,圖表上方的區域並非凸集:

嚴格凸函數只有一個局部最小值點,這個點也是全域最小值點。傳統的 U 形函式是嚴格凸函式。不過,部分凸函數 (例如直線) 並非 U 形。
詳情請參閱機器學習速成課程中的「收斂和凸函數」。
凸函數最佳化
使用梯度下降等數學技巧,找出凸函數的最小值。機器學習領域的大量研究都著重於將各種問題制定為凸函數最佳化問題,並更有效率地解決這些問題。
如需完整詳細資料,請參閱 Boyd 和 Vandenberghe 的《凸優化》。
凸集
歐幾里得空間的子集,在子集中任意兩點之間繪製的線條,都會完全位於子集中。舉例來說,下列兩個形狀都是凸集:

相較之下,下列兩個形狀並非凸集:

卷積
在數學中,簡單來說,這是兩個函式的混合體。在機器學習中,捲積會混合捲積篩選器和輸入矩陣,以訓練權重。
如果沒有卷積,機器學習演算法就必須為大型張量中的每個儲存格學習個別權重。舉例來說,如果機器學習演算法訓練的圖片大小為 2K x 2K,就必須找出 400 萬個不同的權重。由於採用了捲積,機器學習演算法只需要找出捲積篩選器中每個儲存格的權重,大幅減少訓練模型所需的記憶體。套用捲積濾鏡時,系統會將濾鏡複製到所有儲存格,並與每個儲存格相乘。
詳情請參閱「圖像分類」課程中的「卷積類神經網路簡介」。
卷積濾波器
卷積運算中的其中一個運算元。(另一個參與者是輸入矩陣的切片)。卷積濾波器是與輸入矩陣具有相同等級的矩陣,但形狀較小。舉例來說,如果輸入矩陣為 28x28,則篩選器可以是任何小於 28x28 的 2D 矩陣。
在相片處理中,迴旋篩選器中的所有儲存格通常會設為 1 和 0 的常數模式。在機器學習中,迴旋濾鏡通常會以隨機數字做為種子,然後網路會訓練理想值。
詳情請參閱「圖像分類」課程中的「捲積」。
卷積層
深層類神經網路的層,其中卷積篩選器會沿著輸入矩陣傳遞。舉例來說,請參考下列 3x3 convolutional filter:
![3x3 矩陣,值如下:[[0,1,0], [1,0,1], [0,1,0]]](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalFilter33.svg?authuser=1&hl=zh-tw)
以下動畫顯示由 9 個捲積運算組成的捲積層,這些運算涉及 5x5 輸入矩陣。請注意,每個捲積運算都會處理輸入矩陣中不同的 3x3 切片。右側產生的 3x3 矩陣包含 9 個捲積運算的結果:
![動畫:顯示兩個矩陣。第一個矩陣是 5x5 矩陣:[[128,97,53,201,198], [35,22,25,200,195],
[37,24,28,197,182], [33,28,92,195,179], [31,40,100,192,177]]。
第二個矩陣是 3x3 矩陣:
[[181,303,618], [115,338,605], [169,351,560]]。
第二個矩陣的計算方式,是在 5x5 矩陣的不同 3x3 子集套用 [[0, 1, 0], [1, 0, 1], [0, 1, 0]] 卷積篩選器。](https://developers.google.com/static/machine-learning/glossary/images/AnimatedConvolution.gif?authuser=1&hl=zh-tw)
詳情請參閱圖片分類課程中的「全連線層」。
卷積類神經網路
類神經網路,其中至少有一層是卷積層。典型的捲積類神經網路是由下列幾種層的組合構成:
卷積類神經網路在特定類型的問題 (例如圖片辨識) 中,已獲得極大的成功。
卷積運算
以下兩步驟數學運算:
- 卷積濾波器和輸入矩陣切片的元素乘法。(輸入矩陣的切片與捲積篩選器具有相同的等級和大小)。
- 結果產品矩陣中所有值的總和。
舉例來說,請看以下 5x5 輸入矩陣:
![5x5 矩陣:[[128,97,53,201,198], [35,22,25,200,195],
[37,24,28,197,182], [33,28,92,195,179], [31,40,100,192,177]]。](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerInputMatrix.svg?authuser=1&hl=zh-tw)
現在,假設有以下 2x2 卷積篩選器:
![2x2 矩陣:[[1, 0], [0, 1]]](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerFilter.svg?authuser=1&hl=zh-tw)
每個捲積運算都涉及輸入矩陣的單一 2x2 切片。舉例來說,假設我們使用輸入矩陣左上方的 2x2 配量。因此,這個切片的捲積運算如下所示:
![將 [[1, 0], [0, 1]] 卷積濾鏡套用至輸入矩陣的左上角 2x2 區段,即 [[128,97], [35,22]]。卷積濾波器會保留 128 和 22,但會將 97 和 35 歸零。因此,迴旋運算會產生值 150 (128+22)。](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerOperation.svg?authuser=1&hl=zh-tw)
卷積層是由一系列卷積運算組成,每個運算都會作用於輸入矩陣的不同切片。
費用
loss 的同義詞。
共同訓練
半監督式學習方法在符合下列所有條件時特別實用:
共同訓練基本上是將獨立信號放大為更強的信號。 舉例來說,假設有分類模型,可將個別二手車分類為「良好」或「不良」。一組預測特徵可能著重於車輛的年份、品牌和型號等匯總特徵;另一組預測特徵可能著重於前車主的駕駛記錄和車輛的維修記錄。
Blum 和 Mitchell 撰寫的結合有標籤和無標籤資料進行共同訓練,是共同訓練的開創性論文。
反事實公平性
這項公平性指標會檢查分類模型是否會為兩位使用者產生相同結果。這兩位使用者完全相同,只差在一或多個敏感屬性。評估反事實公平性的分類模型是找出模型中潛在偏差來源的方法之一。
詳情請參閱下列任一文章:
涵蓋偏誤
請參閱選擇偏誤。
crash blossom
意義不明的句子或詞組。 在自然語言理解方面,崩潰花會造成重大問題。舉例來說,標題「Red Tape Holds Up Skyscraper」(官僚主義阻礙摩天大樓興建)就是一個 crash blossom,因為 NLU 模型可能會從字面或比喻的角度解讀這個標題。
評論家
與深度 Q 網路同義。
交叉熵
對數損失的一般化,適用於多重分類問題。交叉熵可量化兩種機率分布之間的差異。另請參閱 困惑度。
交叉驗證
這項機制會測試模型與一或多個非重疊的資料子集,藉此估算模型對新資料的一般化程度,這些子集會從訓練集中保留。
累積分佈函式 (CDF)
這個函式會定義小於或等於目標值的樣本頻率。舉例來說,請考慮連續值的常態分布。CDF 會告訴您,大約 50% 的樣本應小於或等於平均值,大約 84% 的樣本應小於或等於平均值加上一個標準差。
D
資料分析
考量樣本、評估和視覺化,瞭解資料。在建立第一個模型之前,資料分析特別有用。這項功能對於瞭解實驗和偵錯系統問題也至關重要。
資料擴增
透過轉換現有範例來建立額外範例,人為擴大訓練範例的範圍和數量。舉例來說,假設圖片是其中一項特徵,但資料集沒有足夠的圖片範例,模型無法學習實用的關聯性。理想情況下,您應在資料集中加入足夠的標記圖片,讓模型能正常訓練。如果無法這樣做,資料擴增功能可以旋轉、延展及反映每張圖片,產生原始圖片的許多變體,可能產生足夠的標記資料,以利進行優異的訓練。
DataFrame
DataFrame 類似於表格或試算表。DataFrame 的每個資料欄都有名稱 (標頭),每個資料列則以專屬號碼識別。
DataFrame 中的每個資料欄都採用類似 2D 陣列的結構,但每個資料欄可指派自己的資料型別。
另請參閱官方的 pandas.DataFrame 參考資料頁面。
資料平行處理
一種擴充訓練或推論的方式,可將整個模型複製到多部裝置,然後將輸入資料的子集傳遞至每部裝置。資料平行處理可讓您以非常大的批次大小進行訓練和推論;不過,資料平行處理需要模型夠小,才能在所有裝置上執行。
資料平行化通常可加快訓練和推論速度。
另請參閱模型平行化。
Dataset API (tf.data)
高階 TensorFlow API,用於讀取資料並轉換成機器學習演算法所需的格式。tf.data.Dataset 物件代表元素序列,其中每個元素都包含一或多個 Tensor。tf.data.Iterator 物件可存取 Dataset 的元素。
資料集
原始資料集合,通常 (但不一定) 會以下列其中一種格式整理:
- 試算表
- CSV (半形逗號分隔值) 格式的檔案
決策邊界
模型在二元分類或多元分類問題中學到的類別分隔符。舉例來說,在下圖代表的二元分類問題中,決策邊界是橘色類別和藍色類別之間的界線:

決策樹林
由多個決策樹建立的模型。決策樹林會彙整決策樹的預測結果,藉此做出預測。常見的決策樹林類型包括隨機森林和梯度提升樹狀結構。
詳情請參閱「決策樹」課程的「決策樹」一節。
決策門檻
分類門檻的同義詞。
決策樹狀圖
監督式學習模型,由一組以階層方式排列的條件和葉節點組成。舉例來說,以下是決策樹:
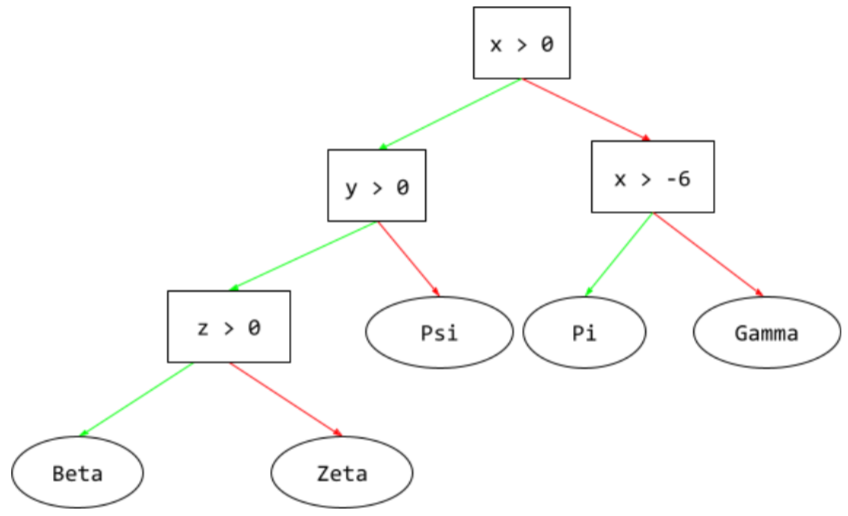
解碼器
一般來說,任何 ML 系統都會從經過處理、密集或內部表示法轉換為更原始、稀疏或外部的表示法。
解碼器通常是較大型模型的元件,經常與編碼器配對。
在序列對序列工作中,解碼器會從編碼器產生的內部狀態開始,預測下一個序列。
如要瞭解 Transformer 架構中的解碼器定義,請參閱 Transformer。
詳情請參閱機器學習速成課程中的大型語言模型。
深度模型
深層模型也稱為深層類神經網路。
與寬模型相比。
便相當熱門的
與「深度模型」同義。
Deep Q-Network (DQN)
在 Q-learning 中,深度類神經網路會預測 Q 函式。
評論家是 Deep Q-Network 的同義詞。
群體均等
舉例來說,如果小人國人和大人國人都申請進入 Glubbdubdrib 大學,只要兩國人錄取率相同,就可達到人口統計均等,無論其中一組的平均資格是否優於另一組。
與均等賠率和機會均等形成對比,後兩者允許分類結果總計取決於私密屬性,但不允許特定基本事實標籤的分類結果取決於私密屬性。如要查看視覺化資料,瞭解以人口統計資料均等性為最佳化目標時的取捨,請參閱「以更智慧的機器學習對抗歧視」。
詳情請參閱機器學習速成課程中的「公平性:人口統計均等」。
降噪
自我監督式學習的常見方法,其中:
去噪功能可讓模型從未標記的樣本中學習。 原始資料集做為目標或標籤,而有雜訊的資料則做為輸入。
部分遮罩語言模型會使用去噪功能,如下所示:
- 系統會遮蓋部分權杖,在未標記的句子中人為加入雜訊。
- 模型會嘗試預測原始權杖。
稠密特徵
特徵:大部分或所有值都是非零值,通常是浮點值的 Tensor。舉例來說,下列 10 元素 Tensor 是密集 Tensor,因為其中 9 個值不為零:
| 8 | 3 | 7 | 5 | 2 | 4 | 0 | 4 | 9 | 6 |
與稀疏特徵形成對比。
密集層
全連接層的同義詞。
深度
類神經網路中的下列項目總和:
舉例來說,如果類神經網路有五個隱藏層和一個輸出層,深度就是 6。
請注意,輸入層不會影響深度。
深度可分離卷積類神經網路 (sepCNN)
以 Inception 為基礎的卷積類神經網路架構,但 Inception 模組會替換為深度可分離的卷積。也稱為 Xception。
深度可分離式捲積 (也簡稱為可分離式捲積) 會將標準 3D 捲積分解為兩個獨立的捲積運算,運算效率更高:首先是深度捲積,深度為 1 (n ✕ n ✕ 1),然後是點向捲積,長度和寬度為 1 (1 ✕ 1 ✕ n)。
詳情請參閱「Xception:Deep Learning with Depthwise Separable Convolutions」。
衍生標籤
代理標籤的同義詞。
裝置
這個詞彙有兩種可能的定義:
- 可執行 TensorFlow 工作階段的硬體類別,包括 CPU、GPU 和 TPU。
- 在加速器晶片 (GPU 或 TPU) 上訓練機器學習模型時,系統中實際操控張量和嵌入的部分。裝置使用加速器晶片。相較之下,主機通常在 CPU 上執行。
差異化隱私
在機器學習中,匿名化方法可保護模型訓練集中包含的任何私密資料 (例如個人資訊),避免這類資料外洩。這個做法可確保模型不會學習或記住特定個人的資訊。具體做法是在模型訓練期間取樣並加入雜訊,模糊化個別資料點,降低揭露機密訓練資料的風險。
差異化隱私也適用於機器學習以外的領域。舉例來說,資料科學家有時會使用差異隱私,在計算不同人口統計資料的產品使用統計資料時,保護個人隱私。
降低維度
減少用於表示特徵向量中特定特徵的維度數量,通常是透過轉換為嵌入向量。
尺寸
具有下列任一定義的過載字詞:
Tensor中的座標層級數量。例如:
- 純量沒有維度,例如
["Hello"]。 - 向量只有一個維度,例如
[3, 5, 7, 11]。 - 矩陣有兩個維度,例如
[[2, 4, 18], [5, 7, 14]]。 您可以使用一個座標,在單一維度向量中指定特定儲存格;您需要兩個座標,才能在二維矩陣中指定特定儲存格。
- 純量沒有維度,例如
特徵向量中的項目數量。
嵌入層中的元素數量。
直接提示
與零樣本提示同義。
離散特徵
特徵,可能的值數量有限。舉例來說,如果特徵的值只能是「動物」、「蔬菜」或「礦物」,就是離散 (或類別) 特徵。
與連續性特徵形成對比。
判別式模型
模型:從一或多個特徵預測標籤。更正式地來說,判別式模型會根據特徵和權重,定義輸出內容的條件機率,也就是:
p(output | features, weights)
舉例來說,如果模型會根據特徵和權重預測電子郵件是否為垃圾郵件,就是判別式模型。
絕大多數的監督式學習模型 (包括分類和迴歸模型) 都是判別式模型。
與生成模型形成對比。
鑑別器
判斷範例是真實還是虛假的系統。
或者,生成對抗網路中的子系統會判斷產生器建立的示例是真實還是虛假。
詳情請參閱 GAN 課程中的鑑別器。
不當影響
對不同人口子群組造成不成比例影響的決策。這通常是指演算法決策程序對某些子群組造成的傷害或好處,大於對其他子群組的影響。
舉例來說,假設某演算法會根據小人國居民的郵寄地址是否包含特定郵遞區號,判斷他們是否符合微型房屋貸款資格,並傾向將他們歸類為「不符合資格」。如果大端序小人國居民比小端序小人國居民更可能擁有這個郵遞區號的郵寄地址,則這項演算法可能會造成差異影響。
與差別待遇不同,後者著重於因演算法決策程序明確輸入子群組特徵而造成的差異。
差別待遇
將主體的敏感屬性納入演算法決策程序,導致不同的人群子群組受到不同待遇。
舉例來說,假設某個演算法會根據小人國居民在貸款申請中提供的資料,判斷他們是否符合微型房屋貸款的資格。如果演算法使用 Lilliputian 的所屬關係 (Big-Endian 或 Little-Endian) 做為輸入內容,則會沿著該維度實施差別待遇。
與差異影響不同,後者著重於演算法決策對子群組的社會影響差異,無論這些子群組是否為模型的輸入內容。
蒸餾
將模型 (稱為「老師」) 縮減為較小的模型 (稱為「學生」),並盡可能忠實地模擬原始模型的預測結果。精煉技術相當實用,因為相較於大型模型 (老師),小型模型有兩項主要優點:
- 推論時間縮短
- 減少記憶體和能源用量
不過,學生的預測結果通常不如老師的預測結果。
精煉會訓練學生模型,盡可能降低損失函式,這是根據學生和老師模型預測結果的差異而定。
比較蒸餾與下列詞彙的異同:
詳情請參閱機器學習速成課程中的「LLM:微調、蒸餾和提示工程」。
發布
特定特徵或標籤的不同值頻率和範圍。分布會擷取特定值的可能性。
下圖顯示兩個不同分布的直方圖:
- 左側是財富與擁有該財富的人數的冪律分布。
- 右側是身高與擁有該身高的人數的常態分布。
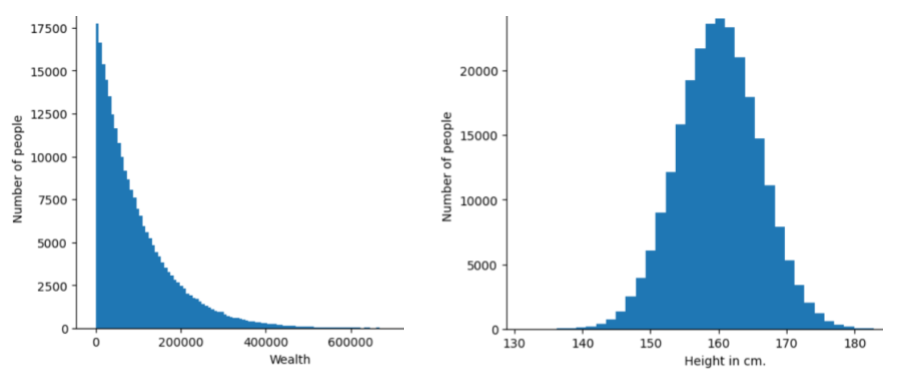
瞭解各項特徵和標籤的分布情形,有助於判斷如何正規化值及偵測離群值。
「超出分布範圍」是指資料集中沒有或極少出現的值。舉例來說,如果資料集包含貓咪圖片,土星圖片就會被視為超出分布範圍。
分裂式分群
請參閱階層式分群。
向下取樣
這個詞彙有多重含意,可能指下列任一情況:
- 減少特徵中的資訊量,以更有效率地訓練模型。舉例來說,在訓練圖像辨識模型前,先將高解析度圖片降採樣為低解析度格式。
- 訓練時,如果過度代表類別的範例所占比例過低,模型訓練成效可能會受到影響。舉例來說,在類別不平衡的資料集中,模型往往會大量學習多數類別的特徵,但少數類別的特徵則學得不夠。欠採樣有助於平衡多數和少數類別的訓練量。
詳情請參閱機器學習速成課程中的「資料集:不平衡的資料集」。
DQN
深層 Q 網路的縮寫。
丟棄正則化
一種正規化形式,有助於訓練類神經網路。Dropout 正規化會移除網路層中固定數量的隨機選取單元,以進行單一梯度步驟。退出單元越多,正規化就越強。這類似於訓練網路,模擬指數級龐大的小型網路集合。如需完整詳細資料,請參閱Dropout:A Simple Way to Prevent Neural Networks from Overfitting。
動態
經常或持續進行的動作。 在機器學習中,「動態」和「線上」是同義詞。 以下是機器學習中「動態」和「線上」的常見用途:
- 動態模型 (或線上模型) 是指經常或持續重新訓練的模型。
- 動態訓練 (或線上訓練) 是指頻繁或持續訓練的過程。
- 動態推論 (或線上推論) 是指依需求產生預測的程序。
動態模型
經常 (甚至持續) 重新訓練的模型。動態模型是「終身學習者」,會不斷適應不斷變化的資料。動態模型也稱為「線上模型」。
與靜態模型比較。
E
Eager Execution
TensorFlow 程式設計環境,可立即執行作業。相反地,在圖形執行中呼叫的作業,要等到明確評估後才會執行。即時執行是命令式介面,與大多數程式設計語言中的程式碼非常相似。一般來說,相較於圖形執行程式,Eager Execution 程式更容易偵錯。
提早停止
一種正規化方法,涉及在訓練損失停止下降前結束訓練。在提早停止訓練中,當驗證資料集的損失開始增加時,您會刻意停止訓練模型;也就是一般化效能變差時。
與提早結束形成對比。
推土機距離 (EMD)
用來評估兩個分布的相對相似度。 地球移動距離越小,表示分布越相似。
編輯距離
用來衡量兩個字串的相似程度。 在機器學習中,編輯距離有以下用途:
- 編輯距離很容易計算。
- 編輯距離可比較兩個已知相似的字串。
- 編輯距離可判斷不同字串與指定字串的相似程度。
編輯距離有多種定義,每種定義都使用不同的字串作業。請參閱 Levenshtein 距離範例。
Einsum 標記法
有效率的標記,用於說明如何合併兩個張量。張量合併方式為將一個張量的元素乘以另一個張量的元素,然後加總乘積。Einsum 標記會使用符號來識別每個張量的軸,並重新排列這些符號,以指定新結果張量的形狀。
NumPy 提供常見的 Einsum 實作。
嵌入層
這是一種特殊的隱藏層,會訓練高維度類別特徵,逐步學習低維度嵌入向量。與僅根據高維度類別特徵訓練相比,嵌入層可讓類神經網路更有效率地訓練。
舉例來說,Google 地球目前支援約 73,000 種樹木。假設樹種是模型中的特徵,因此模型的輸入層包含 73,000 個元素的單熱向量。舉例來說,baobab 可能會以類似下列方式表示:

73,000 個元素的陣列非常長,如果沒有在模型中加入嵌入層,由於要將 72,999 個零相乘,訓練過程會非常耗時。假設您選擇的嵌入層包含 12 個維度,因此,嵌入層會逐步學習每種樹木的新嵌入向量。
在某些情況下,雜湊是嵌入層的合理替代方案。
詳情請參閱機器學習速成課程中的嵌入。
嵌入空間
特徵會從高維度向量空間對應至 d 維度向量空間。嵌入空間經過訓練,可擷取對預期應用程式有意義的結構。
兩個嵌入的點積是衡量相似度的指標。
嵌入向量
廣義來說,這是取自任何 隱藏層的浮點數陣列,用於描述該隱藏層的輸入內容。嵌入向量通常是嵌入層中訓練的浮點數陣列。舉例來說,假設嵌入層必須為地球上 73,000 種樹木學習嵌入向量。以下陣列可能是猴麵包樹的嵌入向量:

嵌入向量並非一堆隨機數字,嵌入層會透過訓練決定這些值,類似於類神經網路在訓練期間學習其他權重的方式。陣列的每個元素都是樹種某項特徵的分數。哪個元素代表哪種樹木的特徵?這對人類來說非常難以判斷。
嵌入向量的數學意義在於,相似項目會有一組相似的浮點數。舉例來說,相似的樹種比不相似的樹種,有更相似的浮點數集。紅木和巨杉是相關樹種,因此與紅木和椰子樹相比,兩者會有一組更相似的浮點數。即使使用相同的輸入內容重新訓練模型,嵌入向量中的數字每次都會變更。
實證累積分佈函式 (eCDF 或 EDF)
根據實際資料集的實證測量結果,建立累積分布函數。沿著 x 軸的任何一點,函式的值都是資料集中小於或等於指定值的觀測值比例。
經驗風險最小化 (ERM)
選擇可將訓練集損失降到最低的函式。與結構風險最小化形成對比。
編碼器
一般來說,任何 ML 系統都會將原始、稀疏或外部表示法轉換為經過處理、較密集或較內部的表示法。
編碼器通常是較大型模型的元件,且經常與解碼器配對。有些 Transformer 會將編碼器與解碼器配對,但其他 Transformer 只會使用編碼器或解碼器。
有些系統會將編碼器的輸出內容做為分類或迴歸網路的輸入內容。
在序列對序列工作中,編碼器會接收輸入序列並傳回內部狀態 (向量)。接著,解碼器會使用該內部狀態預測下一個序列。
如要瞭解 Transformer 架構中的編碼器定義,請參閱 Transformer。
詳情請參閱機器學習速成課程中的「LLM:什麼是大型語言模型」。
endpoints
服務可連線的網路位址 (通常是網址)。
集成
模型集合,這些模型是獨立訓練,預測結果會經過平均或彙整。在許多情況下,集成模型產生的預測結果比單一模型更準確。舉例來說,隨機森林是由多個決策樹建構而成的集成。請注意,並非所有決策樹林都是集合。
詳情請參閱機器學習速成課程中的「隨機森林」。
熵
在 資訊理論中,熵是指機率分布的不可預測程度。或者,熵也可以定義為每個樣本所含的資訊量。當隨機變數的所有值都同樣可能發生時,分配的熵最高。
如果集合有兩個可能的值「0」和「1」(例如二元分類問題中的標籤),則熵的公式如下:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
其中:
- H 是熵。
- p 是「1」範例的分數。
- q 是「0」範例的分數。請注意,q = (1 - p)
- 記錄通常是記錄2。在本例中,熵單位為位元。
舉例來說,假設:
- 100 個範例包含值「1」
- 300 個範例包含值「0」
因此,熵值為:
- p = 0.25
- q = 0.75
- H = (-0.25)log2(0.25) - (0.75)log2(0.75) = 每個範例 0.81 位元
如果資料集完全平衡 (例如 200 個「0」和 200 個「1」),每個樣本的熵為 1.0 位元。如果集合變得不平衡,熵值就會趨近於 0.0。
在決策樹中,熵有助於制定資訊增益,協助分割器在分類決策樹成長期間選取條件。
比較熵值與:
熵通常稱為「香農熵」。
詳情請參閱「使用數值特徵進行二元分類的精確分割器」決策樹課程。
環境
在強化學習中,世界包含代理程式,並允許代理程式觀察該世界的狀態。舉例來說,所代表的世界可以是西洋棋等遊戲,也可以是迷宮等實體世界。當代理對環境套用動作時,環境就會在不同狀態之間轉換。
劇集
Epoch 紀元時間
一個訓練週期代表 N/批量大小
訓練疊代,其中 N 是樣本總數。
舉例來說,假設:
- 資料集包含 1,000 個範例。
- 批次大小為 50 個範例。
因此,單一訓練週期需要 20 次疊代:
1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations
詳情請參閱機器學習速成課程中的「線性迴歸:超參數」。
epsilon greedy 政策
在強化學習中,政策會以 epsilon 概率遵循隨機政策,否則會遵循貪婪政策。舉例來說,如果 epsilon 為 0.9,則政策有 90% 的時間會遵循隨機政策,10% 的時間會遵循貪婪政策。
在連續集數中,演算法會降低 epsilon 的值,以便從遵循隨機政策轉為遵循貪婪政策。透過轉移政策,代理程式會先隨機探索環境,然後貪婪地利用隨機探索的結果。
機會平等
公平性指標,用於評估模型是否能對敏感屬性的所有值,做出同樣準確的預測。換句話說,如果模型的理想結果是正類,目標就是讓所有群組的真陽性率相同。
機會均等與均等勝算有關,兩者都要求所有群組的真陽率和偽陽率相同。
假設 Glubbdubdrib 大學的嚴格數學課程同時招收小人國和大人國的學生。小人國的中學提供紮實的數學課程,絕大多數學生都有資格參加大學課程。Brobdingnagian 的中學完全不提供數學課程,因此合格的學生少得多。如果無論學生是小人國人還是大人國人,只要符合資格,錄取機率都相同,則就國籍 (小人國或大人國) 而言,偏好的「錄取」標籤即符合機會均等原則。
舉例來說,假設有 100 位小人國人和 100 位大人國人申請進入 Glubbdubdrib 大學,而入學決定如下:
表 1. 小人國申請者 (90% 符合資格)
| 晉級 | 不合格 | |
|---|---|---|
| 已錄取 | 45 | 3 |
| 已遭拒 | 45 | 7 |
| 總計 | 90 | 10 |
|
錄取合格學生的百分比:45/90 = 50% 拒絕不合格學生的百分比:7/10 = 70% 錄取小人國學生的總百分比:(45+3)/100 = 48% |
||
表 2. Brobdingnagian 申請者 (10% 符合資格):
| 晉級 | 不合格 | |
|---|---|---|
| 已錄取 | 5 | 9 |
| 已遭拒 | 5 | 81 |
| 總計 | 10 | 90 |
|
符合資格的學生錄取率:5/10 = 50% 不符合資格的學生拒絕率:81/90 = 90% Brobdingnagian 學生總錄取率:(5+9)/100 = 14% |
||
上述例子符合接受合格學生的機會均等原則,因為合格的 Lilliputians 和 Brobdingnagians 都有 50% 的入學機會。
雖然滿足機會均等,但下列兩項公平性指標未達標:
- 群體均等:小人國人和大人國人進入大學的比例不同;小人國學生有 48% 能進入大學,但大人國學生只有 14% 能進入大學。
- 均等機會:符合資格的 Lilliputian 和 Brobdingnagian 學生都有相同的入學機會,但不符合資格的 Lilliputian 和 Brobdingnagian 學生被拒絕的機會相同,這項額外限制並未滿足。不符合資格的 Lilliputian 拒絕率為 70%,不符合資格的 Brobdingnagian 拒絕率則為 90%。
詳情請參閱機器學習速成課程中的「公平性:機會均等」。
等化勝算
這項公平性指標可評估模型是否能針對敏感屬性的所有值,對正類和負類做出同樣準確的預測,而不僅限於其中一類。換句話說,所有群組的真陽率和偽陰率應相同。
均等機會與機會均等相關,後者只著重於單一類別 (正值或負值) 的錯誤率。
舉例來說,假設 Glubbdubdrib 大學的嚴格數學課程同時招收小人國和大腳國的學生。Lilliputians 的中學提供完善的數學課程,絕大多數學生都符合大學課程的資格。Brobdingnagian 的中學完全沒有數學課,因此合格的學生少得多。只要申請人符合資格,無論是小人國或大人國的居民,都有同等機會獲准加入該計畫,若不符合資格,則有同等機會遭到拒絕,即符合均等機會原則。
假設有 100 名小人國人和 100 名大人國人申請進入格魯布達布德里布大學,而入學決定如下:
表 3. 小人國申請者 (90% 符合資格)
| 晉級 | 不合格 | |
|---|---|---|
| 已錄取 | 45 | 2 |
| 已遭拒 | 45 | 8 |
| 總計 | 90 | 10 |
|
符合資格的學生錄取百分比:45/90 = 50% 不符合資格的學生遭拒百分比:8/10 = 80% 錄取的小人國學生總百分比:(45+2)/100 = 47% |
||
表 4. Brobdingnagian 申請者 (10% 符合資格):
| 晉級 | 不合格 | |
|---|---|---|
| 已錄取 | 5 | 18 |
| 已遭拒 | 5 | 72 |
| 總計 | 10 | 90 |
|
符合資格的學生錄取率:5/10 = 50% 不符合資格的學生拒絕率:72/90 = 80% Brobdingnagian 學生總錄取率:(5+18)/100 = 23% |
||
由於符合資格的 Lilliputian 和 Brobdingnagian 學生都有 50% 的入學機會,不符合資格的 Lilliputian 和 Brobdingnagian 學生則有 80% 的機率遭到拒絕,因此滿足了均等機會條件。
「機會均等」的正式定義請參閱「Equality of Opportunity in Supervised Learning」,如下所示:「如果預測值 Ŷ 和受保護屬性 A 相互獨立 (以 Y 為條件),則預測值 Ŷ 會滿足受保護屬性 A 和結果 Y 的機會均等條件。」
Estimator
已淘汰的 TensorFlow API。請改用 tf.keras,而非 Estimator。
evals
主要用來做為大型語言模型評估的縮寫。 廣義來說,評估是任何形式的評估縮寫。
評估
評估模型品質或比較不同模型成效的程序。
如要評估監督式機器學習模型,通常會根據驗證集和測試集進行判斷。評估 LLM 通常需要進行更廣泛的品質和安全評估。
完全比對
這項指標不是 0 就是 1,模型輸出內容必須與基準真相或參照文字完全一致,否則就是 0 分。舉例來說,如果基準真相是「orange」,只有「orange」這個模型輸出結果符合完全比對條件。
完全相符也可以評估輸出為序列 (項目排序清單) 的模型。一般而言,完全相符是指產生的排名清單必須與基準真相完全相符,也就是兩個清單中的每個項目都必須依相同順序排列。不過,如果實際資料包含多個正確序列,只要模型輸出內容與其中一個正確序列相符,即為完全比對。
範例
特徵的一列值,以及可能的標籤。監督式學習中的範例可分為兩大類:
- 「標記範例」包含一或多個特徵和標籤。訓練期間會使用標記範例。
- 未標記的樣本包含一或多個特徵,但不含標籤。推論期間會使用未加上標籤的樣本。
舉例來說,假設您要訓練模型,判斷天氣狀況對學生測驗成績的影響。以下是三個標示範例:
| 功能 | 標籤 | ||
|---|---|---|---|
| 溫度 | 溼度 | 氣壓 | 測驗分數 |
| 15 | 47 | 998 | 不錯 |
| 19 | 34 | 1020 | 極佳 |
| 18 | 92 | 1012 | 不佳 |
以下是三個未標記的範例:
| 溫度 | 溼度 | 氣壓 | |
|---|---|---|---|
| 12 | 62 | 1014 | |
| 21 | 47 | 1017 | |
| 19 | 41 | 1021 |
資料集的資料列通常是範例的原始來源。 也就是說,範例通常包含資料集中的部分資料欄。此外,範例中的特徵也可以包含合成特徵,例如特徵交叉。
詳情請參閱「機器學習簡介」課程中的「監督式學習」。
經驗重播
在強化學習中,DQN 技術用於減少訓練資料中的時間相關性。代理程式會將狀態轉換儲存在重播緩衝區中,然後從重播緩衝區取樣轉換,以建立訓練資料。
實驗者偏誤
請參閱確認偏誤。
梯度爆炸問題
深層類神經網路 (尤其是循環類神經網路) 中的梯度往往會變得異常陡峭 (高),陡峭的梯度通常會導致深度類神經網路中,每個節點的權重出現大幅更新。
如果模型受到梯度爆炸問題影響,訓練就會變得困難或無法進行。漸層剪輯可以減輕這個問題。
請與梯度消失問題比較。
F
F1
真實性
在機器學習領域中,這項屬性用來描述模型,其輸出內容以現實為依據。事實性是概念,而非指標。 舉例來說,假設您將下列提示傳送至大型語言模型:
食鹽的化學式為何?
如果模型著重事實性,則會回覆:
NaCl
我們很容易會認為所有模型都應以事實為依據。 不過,部分提示 (如下所示) 應會促使生成式 AI 模型著重創意,而非事實。
為太空人和毛毛蟲寫一首打油詩。
因此生成的打油詩不太可能符合現實。
與根據事實相反。
公平性限制
對演算法套用限制,確保滿足一或多項公平性定義。公平性限制的例子包括:公平性指標
可衡量的「公平性」數學定義。常用的公平性指標包括:
許多公平性指標互斥,請參閱公平性指標互相衝突。
偽陰性 (FN)
模型錯誤預測負類的例子。舉例來說,模型預測某封電子郵件不是垃圾郵件 (負面類別),但該郵件實際上是垃圾郵件。
偽陰率
模型錯誤預測為負類的實際正類範例比例。下列公式可計算偽陰性率:
詳情請參閱機器學習速成課程中的「門檻和混淆矩陣」。
偽陽性 (FP)
舉例來說,模型錯誤預測正類。舉例來說,模型預測特定電子郵件是垃圾郵件 (正類),但該電子郵件其實不是垃圾郵件。
詳情請參閱機器學習速成課程中的「門檻和混淆矩陣」。
偽陽率 (FPR)
模型錯誤預測為正類的實際負例比例。下列公式可計算出誤報率:
偽陽率是 ROC 曲線的 x 軸。
詳情請參閱機器學習速成課程中的「分類:ROC 和 AUC」。
快速衰減
這項訓練技術可提升大型語言模型的效能。快速衰減是指在訓練期間快速降低學習率。這項策略有助於防止模型過度配適訓練資料,並提升一般化程度。
功能
機器學習模型的輸入變數。範例包含一或多個特徵。舉例來說,假設您要訓練模型,判斷天氣狀況對學生測驗成績的影響。下表顯示三個範例,每個範例都包含三個特徵和一個標籤:
| 功能 | 標籤 | ||
|---|---|---|---|
| 溫度 | 溼度 | 氣壓 | 測驗分數 |
| 15 | 47 | 998 | 92 |
| 19 | 34 | 1020 | 84 |
| 18 | 92 | 1012 | 87 |
與標籤的對比度。
詳情請參閱「機器學習簡介」課程中的「監督式學習」。
特徵交錯
舉例來說,假設「情緒預測」模型會將溫度歸入下列四個類別之一:
freezingchillytemperatewarm
並以以下三種風速之一表示:
stilllightwindy
如果沒有特徵交叉,線性模型會針對上述七個不同區隔分別進行訓練。因此,模型會根據 freezing 訓練,例如,與根據 windy 訓練無關。
或者,您也可以建立溫度和風速的特徵交叉。這個合成特徵會有下列 12 個可能值:
freezing-stillfreezing-lightfreezing-windychilly-stillchilly-lightchilly-windytemperate-stilltemperate-lighttemperate-windywarm-stillwarm-lightwarm-windy
透過特徵交叉,模型可以瞭解freezing-windy天和freezing-still天之間的情緒差異。
如果您從兩個各有很多不同值區的特徵建立合成特徵,產生的特徵交叉會有很多可能的組合。舉例來說,如果一個特徵有 1,000 個值區,另一個特徵有 2,000 個值區,則產生的特徵交叉有 2,000,000 個值區。
正式來說,交叉是笛卡兒乘積。
特徵交叉通常用於線性模型,很少用於類神經網路。
詳情請參閱機器學習速成課程中的類別資料:特徵交叉。
特徵工程
這項程序包含下列步驟:
- 判斷哪些特徵可能適合用來訓練模型。
- 將資料集中的原始資料轉換為這些特徵的有效版本。
舉例來說,您可能會判斷 temperature 是實用的功能。接著,您可以嘗試分組,最佳化模型從不同 temperature 範圍學習的內容。
詳情請參閱機器學習速成課程中的「數值資料:模型如何使用特徵向量擷取資料」。
特徵擷取
多載字詞,定義如下:
特徵重要性
變數重要性的同義詞。
功能集
機器學習模型訓練時所用的特徵群組。舉例來說,預測房價的模型可能只會使用郵遞區號、房產大小和房產狀況等簡單特徵。
功能規格
說明從 tf.Example 通訊協定緩衝區擷取特徵資料所需的資訊。由於 tf.Example 通訊協定緩衝區只是資料的容器,因此您必須指定下列項目:
- 要擷取的資料 (即功能的鍵)
- 資料類型 (例如 float 或 int)
- 長度 (固定或可變)
特徵向量
包含特徵值的陣列,組成範例。特徵向量會在訓練和推論期間輸入。 舉例來說,如果模型有兩個離散特徵,特徵向量可能如下:
[0.92, 0.56]
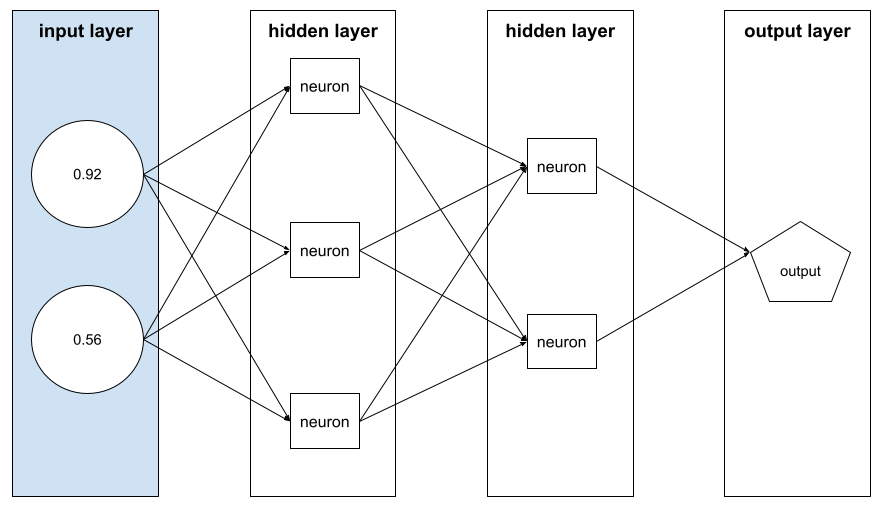
每個範例都會提供特徵向量的不同值,因此下一個範例的特徵向量可能是:
[0.73, 0.49]
特徵工程會決定如何在特徵向量中表示特徵。舉例來說,具有五個可能值的二元類別特徵,可以透過 one-hot 編碼表示。在本例中,特定範例的特徵向量部分會包含四個零,以及第三個位置的單一 1.0,如下所示:
[0.0, 0.0, 1.0, 0.0, 0.0]
再舉一例,假設您的模型包含三項特徵:
- 以 one-hot 編碼表示的二元類別特徵,具有五個可能值,例如:
[0.0, 1.0, 0.0, 0.0, 0.0] - 另一個二元類別特徵,有 3 個可能值,以 one-hot 編碼表示,例如:
[0.0, 0.0, 1.0] - 浮點特徵,例如:
8.3。
在本例中,每個範例的特徵向量會以九個值表示。以上述清單中的範例值為例,特徵向量會是:
0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 8.3
詳情請參閱機器學習速成課程中的「數值資料:模型如何使用特徵向量擷取資料」。
特徵化
從文件或影片等輸入來源擷取特徵,並將這些特徵對應至特徵向量的過程。
聯合學習
分散式的機器學習做法,會使用智慧型手機等裝置上的去中心化示例,訓練機器學習模型。在聯合學習中,部分裝置會從中央協調伺服器下載目前的模型。裝置會使用儲存在裝置上的範例來改良模型。接著,裝置會將模型改良項目 (而非訓練範例) 上傳至協調伺服器,並與其他更新項目匯總,產生改良的全球模型。彙整完成後,就不再需要裝置計算出的模型更新,可以捨棄。
由於訓練範例不會上傳,因此聯合學習遵循專注資料收集和資料最小化原則的隱私權原則。
詳情請參閱聯合學習漫畫 (沒錯,是漫畫)。
回饋循環
在機器學習中,模型預測結果會影響同一模型或其他模型的訓練資料。舉例來說,推薦電影的模型會影響使用者看到的電影,進而影響後續的電影推薦模型。
詳情請參閱機器學習速成課程中的「可供實際工作環境使用的機器學習系統:應提出的問題」。
前饋類神經網路 (FFN)
沒有循環或遞迴連線的類神經網路。舉例來說,傳統的深層類神經網路就是前饋類神經網路。與循環類神經網路 (循環式) 形成對比。
少量樣本學習
這是一種機器學習方法,通常用於物件分類,旨在僅使用少量訓練樣本,訓練出有效的分類模型。
少量樣本提示
提示包含多個 (「幾個」) 範例,說明大型語言模型應如何回應。舉例來說,下列冗長提示包含兩個範例,向大型語言模型說明如何回答查詢。
| 提示的組成部分 | 附註 |
|---|---|
| 指定國家/地區的官方貨幣為何? | 您希望 LLM 回答的問題。 |
| 法國:歐元 | 舉例來說。 |
| 英國:英鎊 | 另一個例子。 |
| 印度: | 實際查詢。 |
一般來說,少量樣本提示比零樣本提示和單樣本提示更能產生理想結果。不過,少量樣本提示需要較長的提示。
詳情請參閱機器學習速成課程中的「提示工程」。
小提琴
以 Python 為主的設定程式庫,可設定函式和類別的值,無需侵入式程式碼或基礎架構。以 Pax 和其他 ML 程式碼集為例,這些函式和類別代表模型、訓練 超參數。
Fiddle 假設機器學習程式碼集通常分為:
- 程式庫程式碼,用於定義層和最佳化器。
- 資料集「膠合」程式碼,可呼叫程式庫並將所有項目連結在一起。
Fiddle 會以未評估且可變動的形式,擷取黏合程式碼的呼叫結構。
微調
對預先訓練模型進行第二階段的特定任務訓練,以便修正相關參數,將模型用於特定用途。舉例來說,部分大型語言模型的完整訓練序列如下:
- 預先訓練:使用大量一般資料集訓練大型語言模型,例如所有英文版 Wikipedia 頁面。
- 微調:訓練預先訓練模型執行特定工作,例如回覆醫療查詢。微調通常需要數百或數千個專注於特定任務的範例。
以大型圖片模型為例,完整的訓練序列如下:
- 預先訓練:使用大量一般圖片資料集 (例如 Wikimedia Commons 中的所有圖片),訓練大型圖片模型。
- 微調:訓練預先訓練模型,執行特定工作,例如生成虎鯨圖片。
微調可包含下列策略的任意組合:
- 修改預先訓練模型的所有現有參數。這有時稱為「完整微調」。
- 只修改預先訓練模型部分現有參數 (通常是與輸出層最接近的層),同時保持其他現有參數不變 (通常是與輸入層最接近的層)。請參閱高效參數調整。
- 新增更多層,通常是在最接近輸出層的現有層上方。
微調是遷移學習的一種形式。 因此,微調作業使用的損失函數或模型類型,可能與訓練預先訓練模型時不同。舉例來說,您可以微調預先訓練的大型圖像模型,產生迴歸模型,傳回輸入圖像中的鳥類數量。
比較微調與下列詞彙的異同:
詳情請參閱機器學習密集課程的「微調」一文。
Flash 模型
這是一系列相對較小的 Gemini 模型,專為速度和低延遲進行最佳化。Flash 模型適用於各種應用程式,可快速回覆並提供高處理量。
亞麻色
以 JAX 為基礎建構的深度學習 程式庫,採用開放原始碼,效能優異。Flax 提供訓練 類神經網路的函式,以及評估網路效能的方法。
Flaxformer
開放原始碼 Transformer 程式庫,以 Flax 為基礎建構,主要用於自然語言處理和多模態研究。
忘記閘道
長期短期記憶單元中,負責調控資訊流經單元的比例。忘記閘會決定要從儲存格狀態捨棄哪些資訊,藉此維護脈絡。
基礎模型
這類預先訓練模型以龐大且多樣化的訓練集訓練而成,基礎模型可以執行下列兩項操作:
換句話說,基礎模型在一般情況下已具備強大能力,但可進一步自訂,以更有效率地完成特定工作。
成功次數比例
用於評估機器學習模型生成文字的指標。 成功率是指「成功」生成的文字輸出內容數量,除以生成的文字輸出內容總數。舉例來說,如果大型語言模型生成 10 個程式碼區塊,其中 5 個成功,則成功率為 50%。
雖然成功率在統計學中廣泛適用,但在 ML 領域中,這項指標主要用於評估可驗證的任務,例如程式碼生成或數學問題。
完整 softmax
softmax 的同義詞。
與候選人抽樣形成對比。
詳情請參閱機器學習速成課程中的「類神經網路:多類別分類」。
全連接層
函式轉換
這類函式會將函式做為輸入內容,並傳回轉換後的函式做為輸出內容。JAX 使用函式轉換。
G
GAN
生成對抗網路的縮寫。
Gemini
這個生態系統搭載 Google 最先進的 AI 技術,這個生態系統的元素包括:
- 各種 Gemini 模型。
- 與 Gemini 模型互動的對話式介面。 使用者輸入提示,Gemini 則根據提示回覆。
- 各種 Gemini API。
- 以 Gemini 模型為基礎的各種商用產品,例如 Gemini 版 Google Cloud。
Gemini 模型
Google 最先進的 Transformer 架構多模態模型。Gemini 模型專為整合代理程式而設計。
使用者可以透過各種方式與 Gemini 模型互動,包括透過互動式對話介面和 SDK。
Gemma
這是一系列輕量級開放式模型,採用與建立 Gemini 模型時相同的研究成果和技術。Gemma 提供多種模型,每種模型都具備不同功能,例如視覺、程式碼和指令遵循。詳情請參閱 Gemma。
生成式 AI 或 genAI
生成式 AI 的縮寫。
一般化
模型對先前未見過的新資料做出正確預測的能力。能夠泛化的模型與過度配適的模型相反。
詳情請參閱機器學習速成課程中的「泛化」。
一般化曲線
一般化曲線有助於偵測可能的過度訓練。舉例來說,下列一般化曲線顯示過度訓練,因為驗證損失最終會遠高於訓練損失。
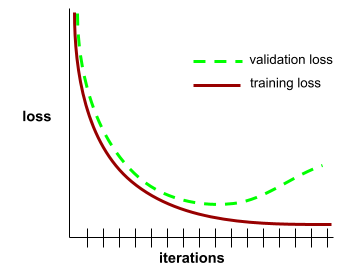
詳情請參閱機器學習速成課程中的「泛化」。
廣義線性模型
最小平方法迴歸模型的泛化,這類模型是以高斯雜訊為基礎,適用於以其他類型雜訊為基礎的其他類型模型,例如卜瓦松雜訊或類別雜訊。廣義線性模型的例子包括:
- 邏輯迴歸
- 多元迴歸
- 最小平方法迴歸
廣義線性模型的參數可透過凸面最佳化找出。
廣義線性模型具有下列屬性:
- 最佳最小平方法迴歸模型的平均預測值,等於訓練資料的平均標籤。
- 最佳邏輯迴歸模型預測的平均機率,等於訓練資料的平均標籤。
廣義線性模型的功能會受到特徵限制。與深層模型不同,廣義線性模型無法「學習新特徵」。
生成的文字
一般來說,這是指機器學習模型輸出的文字。評估大型語言模型時,部分指標會比較生成的文字與參考文字。舉例來說,假設您想判斷機器學習模型將法文翻譯成荷蘭文的成效,在這種情況下:
- 生成文字是機器學習模型輸出的荷蘭文翻譯。
- 參考文字是由人工翻譯人員 (或軟體) 建立的荷蘭文翻譯。
請注意,部分評估策略不涉及參考文字。
生成對抗網路 (GAN)
這類系統會建立新資料,其中生成器會建立資料,鑑別器則會判斷建立的資料是否有效。
詳情請參閱生成對抗網路課程。
生成式 AI
這項新興的變革性領域沒有正式定義。 不過,大多數專家都同意,生成式 AI 模型可以「生成」以下內容:
- 複雜
- 連貫
- 原始圖片
生成式 AI 的例子包括:
- 大型語言模型:可生成精準的原創文字,並回答問題。
- 圖片生成模型,可生成獨特的圖片。
- 音訊和音樂生成模型,可創作原創音樂或生成逼真的語音。
- 影片生成模型,可生成原創影片。
包括 LSTM 和 RNN 在內的部分早期技術,也能生成原創且連貫的內容。部分專家認為這些早期技術就是生成式 AI,但也有人認為真正的生成式 AI 必須能產生比早期技術更複雜的輸出內容。
與預測型機器學習形成對比。
生成模型
實務上,如果模型符合下列任一條件,
- 從訓練資料集建立 (產生) 新範例。 舉例來說,生成式模型可以先以詩集資料集訓練,生成對抗網路的產生器部分屬於這個類別。
- 判斷新樣本來自訓練集的機率,或是由與訓練集相同的機制建立。舉例來說,生成式模型在由英文句子組成的資料集上訓練後,可以判斷新輸入內容是有效英文句子的機率。
從理論上來說,生成式模型可以辨別資料集中範例或特定特徵的分布情形。也就是:
p(examples)
非監督式學習模型屬於生成式模型。
與判別式模型形成對比。
產生器
與判別式模型比較。
吉尼不純度
與熵類似的指標。分割器 會使用從吉尼不純度或熵得出的值,組成用於分類條件的決策樹。 資訊增益是從熵值衍生而來。從吉尼不純度衍生的指標,目前沒有普遍接受的同義詞;不過,這個未命名的指標與資訊增益同樣重要。
吉尼不純度也稱為「吉尼係數」,或簡稱「吉尼」。
黃金資料集
一組手動整理的資料,可擷取基準真相。團隊可使用一或多個黃金資料集評估模型品質。
部分黃金資料集會擷取實際資料的不同子網域。舉例來說,圖片分類的黃金資料集可能會擷取照明條件和圖片解析度。
黃金回覆
2 + 2
理想的回覆如下:
4
Google AI Studio
Google 工具,提供簡單易用的介面,方便您使用 Google 的大型語言模型實驗及建構應用程式。詳情請參閱 Google AI Studio 首頁。
GPT (生成式預先訓練 Transformer)
OpenAI 開發的Transformer 架構大型語言模型系列。
GPT 變體可套用至多種模態,包括:
- 圖像生成 (例如 ImageGPT)
- 文字轉圖像生成 (例如 DALL-E)。
gradient
相對於所有自變數的偏導數向量。在機器學習中,梯度是模型函式的偏導數向量。梯度會指向最陡峭的上升方向。
梯度累積
反向傳播技術,只會在每個週期更新參數,而不是在每次疊代時更新。處理每個迷你批次後,梯度累積會更新梯度累計總和。接著,系統會在處理完該世代的最後一個迷你批次後,根據所有梯度變化總和更新參數。
如果批量遠大於訓練可用的記憶體量,梯度累積就非常實用。如果記憶體是個問題,自然會傾向於縮減批次大小。不過,在一般反向傳播中減少批次大小會增加參數更新次數。梯度累積可讓模型避免記憶體問題,同時維持訓練效率。
梯度提升 (決策) 樹狀結構 (GBT)
這是一種決策樹系,具有下列特點:
詳情請參閱決策樹林課程中的「梯度提升決策樹」。
梯度提升
訓練演算法,訓練弱模型,反覆提升強模型的品質 (減少損失)。舉例來說,線性或小型決策樹模型可能就是弱模型。強大模型會成為先前訓練的所有弱模型的總和。
在最簡單的梯度提升形式中,系統會在每次疊代時訓練弱模型,以預測強模型的損失梯度。接著,系統會減去預測的梯度,藉此更新強大模型的輸出內容,類似於梯度下降。
其中:
- $F_{0}$ 是初始強模型。
- $F_{i+1}$ 是下一個強大模型。
- $F_{i}$ 是目前的強大模型。
- $\xi$ 是介於 0.0 和 1.0 之間的值,稱為縮減率,類似於梯度下降中的學習率。
- $f_{i}$ 是訓練用來預測 $F_{i}$ 損失梯度的弱模型。
梯度提升的現代變體也會在運算中納入損失的二階導數 (黑塞矩陣)。
決策樹通常用做梯度提升中的弱模型。請參閱梯度提升 (決策) 樹狀結構。
梯度裁剪
使用梯度下降法訓練模型時,人工限制 (裁剪) 梯度最大值,是減緩梯度爆炸問題的常用機制。
梯度下降
這項數學技術可盡量減少損失。 梯度下降法會反覆調整權重和偏差,逐步找出可將損失降至最低的最佳組合。
梯度下降法比機器學習更古老,而且古老得多。
詳情請參閱機器學習速成課程中的「線性迴歸:梯度下降」。
圖表
在 TensorFlow 中,這是運算規格。圖中的節點代表作業。邊緣是有方向性的,代表將作業結果 (Tensor) 做為運算元傳遞至另一項作業。使用 TensorBoard 將圖表視覺化。
圖表執行
TensorFlow 程式設計環境,程式會先建構圖表,然後執行該圖表的部分或全部內容。TensorFlow 1.x 的預設執行模式為圖形執行。
與急切執行形成對比。
貪婪政策
實證性
模型屬性,其輸出內容以特定來源資料為依據 (「根據」特定來源資料)。舉例來說,假設您將整本物理教科書當做輸入內容 (「脈絡」) 提供給大型語言模型。然後,您會向該大型語言模型提出物理問題。 如果模型回覆的內容與該教科書的資訊相符,則表示該模型以該教科書為依據。請注意,以事實為依據的模型不一定是事實模型。 舉例來說,輸入的物理教科書可能含有錯誤。
真值
現實。
實際發生的情況。
舉例來說,假設有一個二元分類模型,可預測大學一年級學生是否會在六年內畢業。這個模型的實際資料是學生是否在六年內畢業。
團體歸因偏誤
假設個人特質也適用於該群組的所有人。如果資料收集採用便利抽樣,群組歸因偏誤的影響可能會加劇。如果樣本不具代表性,系統可能會做出與實際情況不符的歸因。
另請參閱外團體同質性偏誤和內團體偏誤。此外,如要瞭解詳情,請參閱機器學習速成課程中的「公平性:偏見類型」。
H
幻覺
生成式 AI 模型會產生看似合理但與事實不符的輸出內容,並聲稱是關於現實世界的陳述。舉例來說,如果生成式 AI 模型聲稱巴拉克‧歐巴馬於 1865 年過世,就是產生錯覺。
雜湊
在機器學習中,分組機制用於類別資料,特別是當類別數量龐大,但資料集中實際出現的類別數量相對較少時。
舉例來說,地球上約有 73,000 種樹木。您可以將 73,000 種樹木分別歸入 73,000 個類別。或者,如果資料集中只有 200 種樹木,您可以使用雜湊將樹木種類分成 500 個值區。
單一儲存區可能包含多種樹木。舉例來說,雜湊可能會將「baobab」和「red maple」這兩種基因不同的物種放在同一個值區。無論如何,雜湊仍是將大型類別集對應至所選儲存區數量的好方法。雜湊會以確定性方式將值分組,將具有大量可能值的類別特徵轉換為數量少得多的值。
詳情請參閱機器學習速成課程中的「類別資料:詞彙和獨熱編碼」。
經驗法則
簡單且快速解決問題的方案。舉例來說,「我們使用啟發式方法,準確率達到 86%。改用深層類神經網路後,準確率提升至 98%。
隱藏層
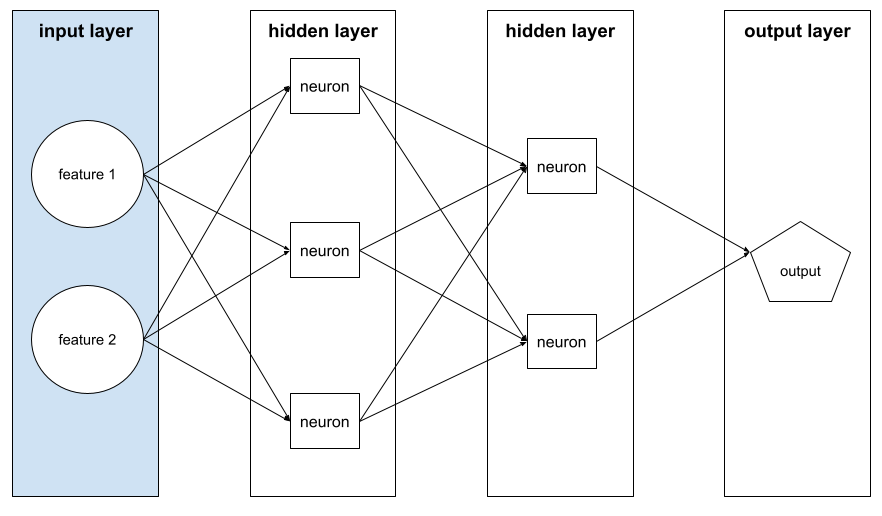
類神經網路中的層,介於輸入層 (特徵) 和輸出層 (預測) 之間。每個隱藏層都包含一或多個神經元。 舉例來說,下列類神經網路包含兩個隱藏層,第一個隱藏層有三個神經元,第二個隱藏層有兩個神經元:
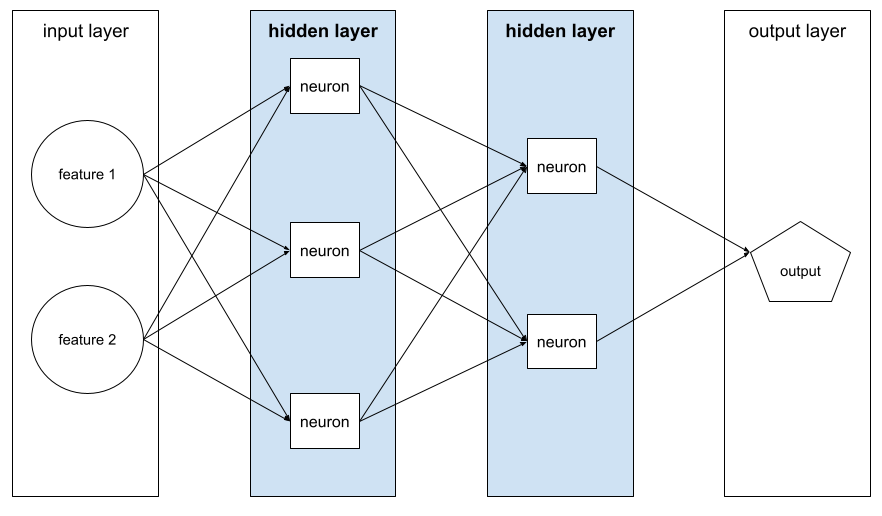
深層類神經網路含有多個隱藏層。舉例來說,上圖是深層類神經網路,因為模型包含兩個隱藏層。
詳情請參閱機器學習速成課程中的「類神經網路:節點和隱藏層」。
階層式分群
這類叢集演算法會建立叢集樹狀結構。階層式叢集非常適合階層式資料,例如植物分類。階層式分群演算法分為兩種:
- 凝聚式分群法會先將每個樣本指派至各自的叢集,然後反覆合併最接近的叢集,建立階層式樹狀結構。
- 分裂式分群會先將所有範例分到一個群組,然後以疊代方式將群組劃分為階層樹狀結構。
與以質心為準的叢集形成對比。
詳情請參閱分群課程中的分群演算法。
爬坡
這項演算法會反覆改良機器學習模型 (「上坡」),直到模型不再進步 (「抵達山頂」) 為止。演算法的一般形式如下:
- 建構起始模型。
- 稍微調整訓練或微調方式,即可建立新的候選模型。這可能需要使用略有不同的訓練集或不同的超參數。
- 評估新的候選模型,並採取下列任一做法:
- 如果候選模型的成效優於起始模型,該候選模型就會成為新的起始模型。在這種情況下,請重複步驟 1、2 和 3。
- 如果沒有任何模型優於起始模型,表示您已達到最佳狀態,應停止疊代。
如需超參數調整指南,請參閱深度學習調整手冊。如需特徵工程的指引,請參閱機器學習密集課程的資料模組。
轉折損失
一系列用於分類的損失函式,旨在找出與每個訓練範例盡可能遠的決策邊界,進而盡量擴大範例與邊界之間的間距。KSVM 使用鉸鏈損失 (或平方鉸鏈損失等相關函式)。如果是二元分類,鉸鏈損失函式的定義如下:
其中 y 是實際標籤 (為 -1 或 +1),y' 則是分類模型的原始輸出內容:
因此,鉸鏈損失與 (y * y') 的關係圖如下所示:

歷史偏誤
一種存在於現實世界並已進入資料集的偏誤。這些偏誤往往會反映現有的文化刻板印象、人口統計不平等,以及對特定社會群體的偏見。
舉例來說,假設分類模型會預測貸款申請人是否會違約,而該模型是根據 1980 年代兩個不同社群中當地銀行的貸款違約歷來資料訓練而成。如果社群 A 的申請人過去的貸款違約機率是社群 B 申請人的六倍,模型可能會學到歷史偏見,導致模型不太可能核准社群 A 的貸款,即使導致該社群違約率較高的歷史條件已不再適用。
詳情請參閱機器學習速成課程的「公平性:偏見類型」一文。
保留資料
範例:訓練期間刻意不使用 (「保留」) 的範例。 驗證資料集和測試資料集都是保留資料的例子。保留資料有助於評估模型推論訓練資料以外資料的能力。與訓練集上的損失相比,保留集上的損失能更準確地估算未見資料集上的損失。
主機
在加速器晶片 (GPU 或 TPU) 上訓練 ML 模型時,系統中負責控制下列兩項作業的部分:
- 程式碼的整體流程。
- 輸入管道的擷取和轉換作業。
主機通常在 CPU 上執行,而不是在加速器晶片上執行;裝置會在加速器晶片上操控張量。
人工評估
由人員判斷機器學習模型輸出內容的品質,例如請雙語者評估機器學習翻譯模型的品質。如果模型沒有唯一正確答案,人工評估就特別有用。
人機迴圈 (HITL)
這個成語的定義較為寬鬆,可能代表下列任一情況:
- 以批判或懷疑的態度看待生成式 AI 輸出內容的政策。
- 確保使用者協助塑造、評估及改善模型行為的策略或系統。人機迴圈可讓 AI 同時運用機器智慧和人類智慧。舉例來說,在 AI 生成程式碼後,由軟體工程師審查的系統,就是人為迴路系統。
超參數
您或超參數調整服務 (例如 Vizier) 在連續執行模型訓練時調整的變數。舉例來說,學習率就是超參數。您可以在一個訓練階段前將學習率設為 0.01。如果判定 0.01 過高,您或許可以在下一個訓練工作階段將學習率設為 0.003。
詳情請參閱機器學習速成課程中的「線性迴歸:超參數」。
超平面
將空間分成兩個子空間的界線。舉例來說,在二維空間中,直線是超平面;在三維空間中,平面是超平面。在機器學習中,超平面通常是分隔高維空間的界線。核方法支持向量機會使用超平面將正向類別與負向類別分開,通常是在非常高維度的空間中。
I
獨立同分布
獨立同分布的縮寫。
圖片辨識
這項程序會分類圖片中的物件、模式或概念。圖像辨識也稱為「圖像分類」。
詳情請參閱機器學習實習:圖片分類。
詳情請參閱 ML Practicum:圖片分類課程。
不平衡資料集
與類別不平衡資料集同義。
隱性偏誤
根據自己的思考模式和記憶,自動建立關聯或做出假設。隱性偏見可能會影響下列事項:
- 資料的收集和分類方式。
- 機器學習系統的設計與開發方式。
舉例來說,建構分類模型來識別婚禮相片時,工程師可能會使用相片中是否有白色禮服做為特徵。不過,白色禮服僅在特定時代和文化中是習俗。
另請參閱確認偏誤。
插補法
值插補的簡短形式。
公平性指標互相衝突
某些公平性概念互不相容,無法同時滿足。因此,沒有單一指標可套用至所有機器學習問題,用來量化公平性。
雖然這可能令人沮喪,但公平性指標不相容並不代表公平性工作毫無成果。而是建議根據特定機器學習問題的發生情境來定義公平性,以避免發生與應用實例相關的危害。
如要進一步瞭解公平性指標互相衝突的問題,請參閱「On the (im)possibility of fairness」(公平性的可能性)。
情境學習
少量樣本提示的同義詞。
獨立同分布 (i.i.d)
從不會變更的分配方式中提取資料,且提取的每個值都不會取決於先前提取的值。i.i.d. 是機器學習的理想氣體,是實用的數學建構,但幾乎不會在現實世界中完全符合。舉例來說,網頁訪客的分布情形可能在短時間內呈現 i.i.d.,也就是說,分布情形在短時間內不會改變,且一個人的造訪行為通常不會影響另一個人的造訪行為。不過,如果擴大時間範圍,網頁訪客人數可能會出現季節性差異。
另請參閱非平穩性。
個人公平性
這項公平性指標會檢查類似的個人是否獲得類似的分類。舉例來說,Brobdingnagian Academy 可能想確保兩名成績和標準化測驗分數相同的學生,獲得入學許可的機率相同,藉此滿足個人公平性。
請注意,個別公平性完全取決於您如何定義「相似性」(在本例中為成績和測驗分數),如果相似性指標遺漏重要資訊 (例如學生的課程嚴謹程度),您可能會引發新的公平性問題。
如要進一步瞭解個別公平性,請參閱「透過認知實現公平性」。
推論
在傳統機器學習中,預測過程是指將訓練好的模型套用至未標記的樣本。如要瞭解詳情,請參閱「機器學習簡介」課程中的「監督式學習」。
在大型語言模型中,推論是指使用訓練好的模型,針對輸入的提示生成回覆的過程。
在統計學中,「推論」的意義略有不同。詳情請參閱 有關統計推論的維基百科文章。
推論路徑
在決策樹中,推論期間,特定範例會從根到其他條件,最後以葉節點終止。舉例來說,在下列決策樹中,較粗的箭頭顯示具有下列特徵值的範例推論路徑:
- x = 7
- y = 12
- z = -3
下圖中的推論路徑會經過三種情況,最後抵達葉節點 (Zeta)。
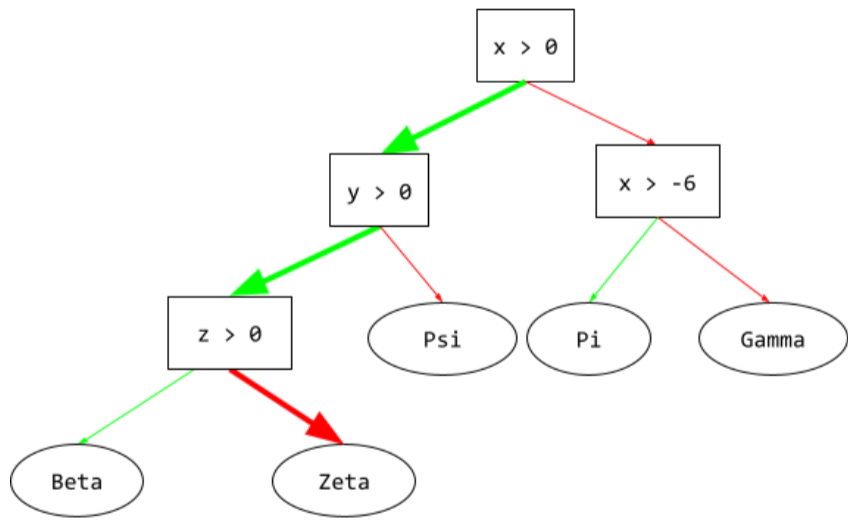
三條粗箭頭代表推論路徑。
詳情請參閱「決策樹林」課程中的決策樹。
資訊增益
在決策樹林中,節點的熵與其子項節點熵的加權 (依範例數量) 總和之間的差異。節點的熵是該節點中範例的熵。
舉例來說,請考量下列熵值:
- 父節點的熵 = 0.6
- 一個子節點的熵 (16 個相關範例) = 0.2
- 另一個子節點的熵 (24 個相關範例) = 0.1
因此,40% 的範例位於一個子節點,60% 位於另一個子節點。因此:
- 子節點的加權熵總和 = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
因此,資訊增益為:
- 資訊增益 = 父項節點的熵 - 子項節點的加權熵總和
- 資訊增益 = 0.6 - 0.14 = 0.46
內團體偏誤
偏好自己所屬的群體或特徵。如果測試人員或評估人員是機器學習開發人員的朋友、家人或同事,則可能出現同群體偏誤,導致產品測試或資料集無效。
內團體偏誤是團體歸因偏誤的一種形式。另請參閱「外團體同質性偏誤」。
詳情請參閱機器學習速成課程的「公平性:偏見類型」一文。
輸入內容生成器
將資料載入類神經網路的機制。
輸入產生器可視為負責將原始資料處理為張量的元件,並反覆運算這些張量,為訓練、評估和推論產生批次。
輸入層
類神經網路的層,其中包含特徵向量。也就是說,輸入層會提供範例,用於訓練或推論。舉例來說,下列神經網路的輸入層包含兩項特徵:
在集合中
在決策樹中,條件會測試一組項目中是否包含某個項目。舉例來說,以下是集合內條件:
house-style in [tudor, colonial, cape]
在推論期間,如果房屋樣式 特徵 的值為 tudor、colonial 或 cape,則此條件會評估為「是」。如果房屋風格特徵的值為其他內容 (例如 ranch),這項條件就會評估為「否」。
與測試 one-hot 編碼特徵的條件相比,集合內條件通常會產生效率更高的決策樹。
執行個體
example 的同義詞。
調整指示
這是一種微調形式,可提升生成式 AI 模型遵循指令的能力。指令調整是指使用一系列指令提示訓練模型,通常涵蓋各種工作。經過指令微調的模型通常會針對各種任務的零樣本提示,生成實用的回應。
比較對象:
可解釋性
以人類可理解的用語,說明或呈現機器學習模型的推理過程。
舉例來說,大多數線性迴歸模型都具有高度可解讀性。(您只需查看每個特徵的訓練權重。)決策樹林也具有高度可解讀性。不過,部分模型仍需轉繪成複雜的圖表,才具有可解釋性。
您可以使用學習技術可解釋性工具 (LIT) 解讀機器學習模型。
資料標註一致性
這項指標可衡量資料標註人員執行工作時,判定一致的頻率。 如果評估人員意見不一致,可能需要改善工作指示。 有時也稱為「註解者間一致性」或「評估者間信度」。另請參閱 Cohen's kappa,這是最受歡迎的評估者間一致性測量方式之一。
詳情請參閱機器學習速成課程中的「類別資料:常見問題」。
交併比 (IoU)
兩個集合的交集除以聯集。在機器學習圖片偵測工作中,交併比用於測量模型預測定界框相對於實際資料定界框的準確度。在這種情況下,兩個方塊的 IoU 是重疊區域與總面積的比率,值介於 0 (預測定界框和實際定界框沒有重疊) 到 1 (預測定界框和實際定界框的座標完全相同) 之間。
舉例來說,在下圖中:
- 預測的定界框 (模型預測畫作中床頭櫃所在位置的座標) 會以紫色標示。
- 實際資料的邊界框 (標示畫中夜間桌子實際位置的座標) 會以綠色標示。
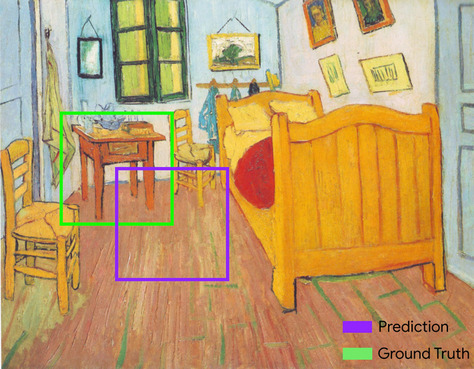
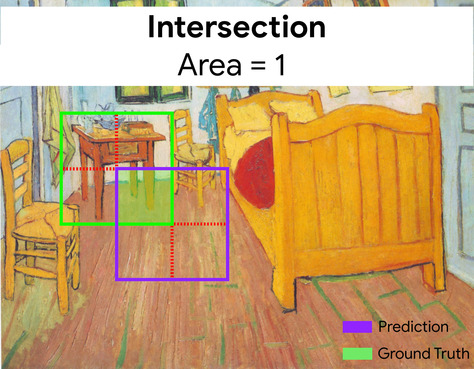
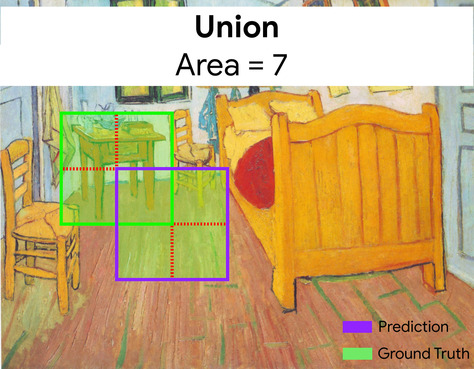
在此,預測和實際資料的定界框交集 (左下) 為 1,預測和實際資料的定界框聯集 (右下) 為 7,因此 IoU 為 \(\frac{1}{7}\)。
IoU
交集與聯集比的縮寫。
項目矩陣
在推薦系統中,矩陣分解會產生嵌入向量矩陣,其中包含每個項目的潛在信號。項目矩陣的每一列都包含所有項目的單一潛在特徵值。舉例來說,假設有電影推薦系統。項目矩陣中的每個資料欄都代表一部電影。潛在信號可能代表類型,也可能是不易解讀的信號,涉及類型、明星、電影年齡或其他因素之間的複雜互動。
項目矩陣的欄數與要分解的目標矩陣相同。舉例來說,假設電影推薦系統評估了 10,000 部電影,項目矩陣就會有 10,000 個資料欄。
項目
在推薦系統中,系統會推薦實體。舉例來說,影片是影視商店推薦的項目,書籍則是書店推薦的項目。
疊代
在訓練期間,模型的參數 (模型的權重和偏差) 會單次更新。批次大小會決定模型在單次疊代中處理的樣本數量。舉例來說,如果批次大小為 20,模型會先處理 20 個範例,再調整參數。
訓練類神經網路時,單一疊代會涉及下列兩次傳遞:
- 前向傳遞,用於評估單一批次的損失。
- 反向傳播 (反向傳播),根據損失和學習率調整模型參數。
詳情請參閱機器學習密集課程中的梯度下降。
J
JAX
陣列運算程式庫,結合 XLA (加速線性代數) 和自動微分,提供高效能的數值運算。JAX 提供簡單又強大的 API,可使用可組合的轉換來編寫加速的數值程式碼。JAX 提供下列功能:
grad(自動微分)jit(即時編譯)vmap(自動向量化或批次處理)pmap(平行化)
JAX 是一種語言,用於表示和組合數值程式碼的轉換,類似於 Python 的 NumPy 程式庫,但範圍廣大得多。(事實上,JAX 底下的 .numpy 程式庫是功能相同的 Python NumPy 程式庫,但完全經過重新編寫)。
JAX 特別適合將模型和資料轉換為適合在 GPU 和 TPU 加速器晶片上平行處理的形式,藉此加快許多機器學習工作的速度。
Flax、Optax、Pax 和許多其他程式庫都是以 JAX 基礎架構為基礎建構而成。
K
Keras
熱門的 Python 機器學習 API。 Keras 可在多種深度學習架構上執行,包括 TensorFlow,並以 tf.keras 的形式提供。
核方法支持向量機 (KSVM)
分類演算法會將輸入資料向量對應至更高維度的空間,盡可能擴大正向和負向類別之間的間距。舉例來說,假設分類問題的輸入資料集有一百個特徵。為盡量擴大正負類別之間的邊界,KSVM 可能會在內部將這些特徵對應至百萬維度空間。KSVM 使用稱為「hinge loss」的損失函式。
關鍵點
圖片中特定特徵的座標。舉例來說,對於可區分花卉品種的圖像辨識模型,關鍵點可能是每個花瓣的中心、花梗、雄蕊等。
k 折交叉驗證
預測模型歸納新資料能力的演算法。k 折交叉驗證中的 k 是指您將資料集範例劃分的相等群組數量,也就是訓練及測試模型 k 次。在每一輪訓練和測試中,測試集都是不同的群組,其餘所有群組則會成為訓練集。經過 k 輪訓練和測試後,計算所選測試指標的平均值和標準差。
舉例來說,假設您的資料集包含 120 個範例。進一步假設您決定將 k 設為 4。因此,在隨機排序範例後,您會將資料集分成四組,每組 30 個範例,並進行四輪訓練和測試:
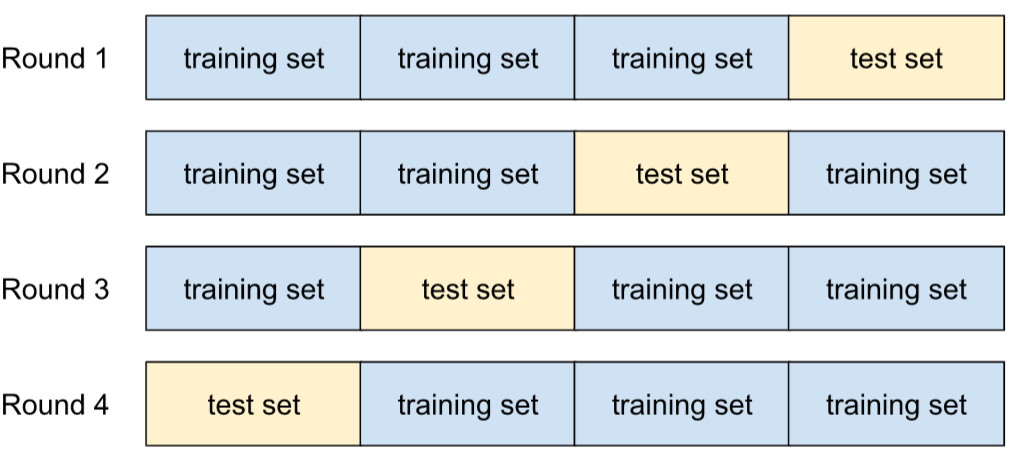
舉例來說,均方誤差 (MSE) 可能是線性迴歸模型最有意義的指標。因此,您會發現所有四輪的 MSE 平均值和標準差。
k-means
在非監督式學習中,這項熱門的分群演算法會將範例分組。k-means 演算法基本上會執行下列操作:
- 反覆判斷最佳 k 個中心點 (稱為質心)。
- 將每個範例指派給最接近的群集中心。最接近相同質心的範例屬於同一群組。
k-means 演算法會選擇群集中心位置,盡量縮短每個範例到最接近群集中心的距離平方累計值。
舉例來說,請思考以下狗狗身高與寬度的圖表:

如果 k=3,k-means 演算法會判斷出三個質心。每個範例都會指派給最接近的群集中心,產生三組:

假設某製造商想為小型、中型和大型犬隻決定理想的毛衣尺寸。這三個質心會找出該叢集中每隻狗的平均高度和平均寬度。因此,製造商可能應根據這三個質心決定毛衣尺寸。請注意,叢集的質心通常不是叢集中的範例。
上圖顯示只有兩項特徵 (高度和寬度) 的範例 k 平均值。請注意,k 平均值可跨多項特徵將範例分組。
詳情請參閱分群課程中的「什麼是 k 平均值分群?」。
k-median
與 k-means 密切相關的分群演算法。這兩者之間的實際差異如下:
- 在 k 平均演算法中,系統會先計算候選質心與每個範例之間的距離,然後找出距離平方總和最小的候選質心,做為最終的質心。
- 在 k 中位數中,決定質心的方式是盡量縮小候選質心與每個範例之間的距離總和。
請注意,距離的定義也不同:
- k-means 會根據從群集中心到範例的歐氏距離,(在二維空間中,歐幾里得距離是指使用畢氏定理計算斜邊。)舉例來說,(2,2) 和 (5,-2) 之間的 k-means 距離為:
- k 中位數會根據從群集中心到範例的 曼哈頓距離,這個距離是每個維度中絕對差異的總和。舉例來說,(2,2) 和 (5,-2) 之間的 k 中位數距離為:
L
L0 正則化
一種正規化類型,會懲罰模型中非零權重的總數。舉例來說,如果模型有 11 個非零權重,受到的懲罰會比有 10 個非零權重的類似模型更重。
L0 正則化有時也稱為 L0 範數正則化。
L1 損失
損失函式,用於計算實際標籤值與模型預測值之間的絕對差異。舉例來說,以下是五個範例的批次 L1 損失計算:
| 範例的實際值 | 模型預測值 | 差異的絕對值 |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L1 損失 | ||
平均絕對誤差是每個樣本的平均 L1 損失。
詳情請參閱機器學習速成課程中的「線性迴歸:損失」。
L1 正則化
一種正規化,會根據權重絕對值的總和,按比例進行加權。L1 正則化有助於將不相關或幾乎不相關特徵的權重設為 0。如果特徵的權重為 0,模型就會有效移除該特徵。
與 L2 正則化的對比。
L2 損失
損失函式:計算實際標籤值與模型預測值之間的差異平方。舉例來說,以下是五個範例的批次 L2 損失計算:
| 範例的實際值 | 模型預測值 | 變量的平方 |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = L2 損失 | ||
由於平方運算,L2 損失會放大離群值的影響。也就是說,相較於 L1 損失,L2 損失對錯誤預測的反應更強烈。舉例來說,前述批次的 L1 損失會是 8 而不是 16。請注意,單一離群值就占了 16 個中的 9 個。
迴歸模型通常會使用 L2 損失做為損失函式。
均方誤差是每個樣本的平均 L2 損失。平方損失是 L2 損失的別名。
詳情請參閱機器學習速成課程中的「邏輯迴歸:損失和正規化」。
L2 正則化
一種正規化,會根據權重平方的總和,按比例懲罰權重。L2 正則化有助於將離群值權重 (高正值或低負值) 調整為接近 0,但不會完全為 0。值非常接近 0 的特徵會保留在模型中,但對模型預測的影響不大。
L2 正則化一律可改善線性模型的一般化作業。
與 L1 正則化的差異。
詳情請參閱機器學習速成課程中的「過度擬合:L2 正規化」。
標籤
每個標示範例都包含一或多個特徵和標籤。舉例來說,在垃圾內容偵測資料集中,標籤可能是「垃圾內容」或「非垃圾內容」。在降雨資料集中,標籤可能是指特定期間的降雨量。
詳情請參閱「機器學習簡介」中的「監督式學習」。
有標籤樣本
包含一或多個特徵和標籤的範例。舉例來說,下表顯示房屋估價模型的三個標籤範例,每個範例都有三個特徵和一個標籤:
| 臥室數量 | 浴室數量 | 房屋屋齡 | 房屋價格 (標籤) |
|---|---|---|---|
| 3 | 2 | 15 | $345,000 |
| 2 | 1 | 72 | $179,000 |
| 4 | 2 | 34 | $392,000 |
在監督式機器學習中,模型會根據加上標籤的範例進行訓練,並對未加上標籤的範例做出預測。
對比有標籤和無標籤的範例。
詳情請參閱「機器學習簡介」中的「監督式學習」。
標籤外洩
模型設計缺陷,其中特徵是標籤的替代項。舉例來說,假設有一個二元分類模型,可預測潛在顧客是否會購買特定產品。假設模型的其中一項特徵是名為 SpokeToCustomerAgent 的布林值。進一步假設客戶服務專員只有在潛在顧客實際購買產品後,才會指派給對方。在訓練期間,模型會快速學習 SpokeToCustomerAgent 與標籤之間的關聯。
詳情請參閱機器學習速成課程中的「監控管道」。
lambda
正規化率的同義詞。
Lambda 是過載的詞彙。本文將著重於正規化中的定義。
LaMDA (對話應用程式的語言模型)
Google 開發的 Transformer 架構大型語言模型,經過大量對話資料集訓練,可生成逼真的對話回覆。
LaMDA:我們的突破性對話技術提供總覽。
地標
與 keypoints 語法相同。
語言模型
詳情請參閱機器學習速成課程中的「什麼是語言模型?」一文。
大型語言模型
至少需要具備大量參數的語言模型。更非正式地來說,任何以 Transformer 為基礎的語言模型,例如 Gemini 或 GPT。
詳情請參閱機器學習速成課程中的大型語言模型 (LLM)。
延遲時間
模型處理輸入內容並生成回覆所需的時間。 高延遲回覆的生成時間比低延遲回覆長。
影響大型語言模型延遲時間的因素包括:
- 輸入和輸出 [token] 長度
- 模型複雜性
- 模型執行的基礎架構
最佳化延遲時間是打造回應迅速且容易使用的應用程式的關鍵。
潛在空間
嵌入空間的同義詞。
圖層
舉例來說,下圖顯示的類神經網路包含一個輸入層、兩個隱藏層和一個輸出層:

在 TensorFlow 中,層也是 Python 函式,會將 Tensor 和設定選項做為輸入內容,並產生其他張量做為輸出內容。
Layers API (tf.layers)
TensorFlow API,用於建構深層類神經網路,做為層的組合。您可以使用 Layers API 建構不同類型的圖層,例如:
tf.layers.Dense,適用於全連接層。tf.layers.Conv2D代表卷積層。
Layers API 遵循 Keras Layers API 慣例。 也就是說,除了前置字元不同之外,Layers API 中的所有函式名稱和簽章,都與 Keras 層 API 中的對應函式相同。
葉子
決策樹中的任何端點。與條件不同,葉節點不會執行測試。而是可能的預測結果。葉節點也是推論路徑的終端節點。
舉例來說,下列決策樹包含三個葉節點:
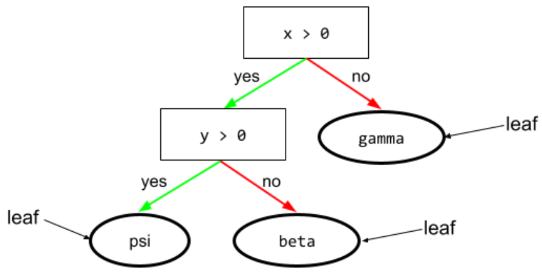
詳情請參閱「決策樹林」課程中的決策樹。
學習技術可解釋性工具 (LIT)
視覺化互動式模型解讀和資料視覺化工具。
您可以使用開放原始碼 LIT 解讀模型,或以視覺化方式呈現文字、圖片和表格資料。
學習率
浮點數,可告知梯度下降演算法,在每次疊代時,權重和偏差值應調整的幅度。舉例來說,學習率為 0.3 時,權重和偏差的調整幅度會是學習率為 0.1 時的三倍。
學習率是重要的超參數。如果學習率設定過低,訓練時間會太長。如果學習率設定過高,梯度下降通常難以達到收斂。
詳情請參閱機器學習速成課程中的「線性迴歸:超參數」。
最小平方法迴歸
Levenshtein 距離
編輯距離指標,可計算將一個字詞變更為另一個字詞所需的最少刪除、插入和替換作業次數。舉例來說,「heart」和「darts」這兩個字之間的 Levenshtein 距離為 3,因為要將一個字變成另一個字,最少需要進行下列三項編輯:
- heart → deart (將「h」替換為「d」)
- deart → dart (刪除「e」)
- dart → darts (插入「s」)
請注意,上述序列並非三項編輯作業的唯一路徑。
線性
兩個或多個變數之間的關係,只能透過加法和乘法表示。
線性關係的圖表是直線。
與非線性比較。
線性模型
模型:為每個特徵指派一個權重,以進行預測。(線性模型也會納入偏差。) 相較之下,深層模型中特徵與預測結果的關係通常是非線性。
相較於深層模型,線性模型通常更容易訓練,且可解讀性更高。不過,深層模型可以學習特徵之間的複雜關係。
線性迴歸
這類機器學習模型符合下列條件:
詳情請參閱機器學習速成課程中的線性迴歸。
LIT
學習技術可解釋性工具 (LIT) 的縮寫,先前稱為語言可解釋性工具。
LLM
大型語言模型的縮寫。
LLM 評估
這是一組指標和基準,用於評估大型語言模型 (LLM) 的效能。概略來說,LLM 評估作業:
- 協助研究人員找出需要改進的 LLM 領域。
- 有助於比較不同 LLM,並找出最適合特定工作的 LLM。
- 確保 LLM 安全且符合道德規範。
詳情請參閱機器學習速成課程中的大型語言模型 (LLM)。
邏輯迴歸
這是一種迴歸模型,可預測機率。邏輯迴歸模型具有下列特性:
- 標籤為類別。邏輯迴歸一詞通常是指二元邏輯迴歸,也就是計算標籤機率的模型,標籤有兩個可能的值。多項式邏輯迴歸是較不常見的變體,可計算標籤的機率,且標籤可有多個可能的值。
- 訓練期間的損失函式為 Log Loss。 (如果標籤有兩個以上的可能值,可以並行放置多個 Log Loss 單位)。
- 模型採用線性架構,而非深層類神經網路。 不過,這項定義的其餘部分也適用於深層模型,這類模型會預測類別標籤的機率。
舉例來說,假設有一個邏輯迴歸模型,可計算輸入電子郵件是垃圾郵件或非垃圾郵件的機率。在推論期間,假設模型預測結果為 0.72。因此,模型會估算:
- 這封電子郵件有 72% 的機率是垃圾郵件。
- 這封電子郵件有 28% 的機率不是垃圾郵件。
邏輯迴歸模型採用下列兩步驟架構:
- 模型會套用輸入特徵的線性函數,產生原始預測結果 (y')。
- 模型會將原始預測結果做為 S 函數的輸入,將原始預測結果轉換為介於 0 到 1 之間的值 (不含 0 和 1)。
與任何迴歸模型一樣,邏輯迴歸模型會預測數字。 不過,這個數字通常會成為二元分類模型的一部分,如下所示:
- 如果預測值大於分類門檻,二元分類模型就會預測正類。
- 如果預測的數字小於分類門檻,二元分類模型會預測負向類別。
詳情請參閱機器學習速成課程中的羅吉斯迴歸。
logits
分類模型產生的原始 (未正規化) 預測向量,通常會傳遞至正規化函式。如果模型要解決多類別分類問題,logit 通常會成為 softmax 函式的輸入內容。 softmax 函式接著會產生 (正規化) 機率向量,每個可能類別各有一個值。
對數損失
詳情請參閱機器學習速成課程中的邏輯迴歸:損失和正規化。
對數勝算比
某個事件發生機率的對數。
長短期記憶 (LSTM)
遞迴類神經網路中的一種儲存格,用於處理應用程式中的資料序列,例如手寫辨識、機器翻譯和圖片說明文字生成。LSTM 會根據新輸入內容和 RNN 中先前儲存格的內容,在內部記憶體狀態中保留記錄,藉此解決訓練 RNN 時因資料序列過長而發生的梯度消失問題。
LoRA
低秩適應的縮寫。
損失
損失函數會計算損失。
詳情請參閱機器學習速成課程中的「線性迴歸:損失」。
損失匯總工具
這是一種機器學習演算法,可結合多個模型的預測結果,並使用這些預測結果進行單一預測,藉此提升模型的效能。因此,損失聚合器可以減少預測的變異數,並提高預測的準確度。
損失曲線
以訓練疊代次數為函式,繪製損失的圖表。下圖顯示典型的損失曲線:
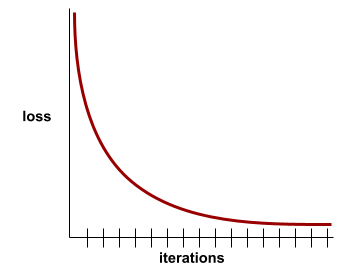
損失曲線可繪製下列所有類型的損失:
另請參閱一般化曲線。
詳情請參閱機器學習速成課程中的「過度擬合:解讀損失曲線」。
損失函數
在訓練或測試期間,計算批次範例損失的數學函式。如果模型預測結果良好,損失函式會傳回較低的損失值;如果模型預測結果不佳,則會傳回較高的損失值。
訓練的目標通常是盡量減少損失函式傳回的損失。
損失函數的種類繁多,請為您要建構的模型類型選擇適當的損失函數。例如:
損失曲面
顯示權重與損失的圖表。梯度下降法的目標是找出損失曲面達到局部最小值時的權重。
中間遺忘效應
LLM 傾向於更有效地使用長情境視窗開頭和結尾的資訊,而非中間的資訊。也就是說,在長脈絡的情況下,中間遺失效應會導致準確度:
- 相對較高:當形成回覆的相關資訊位於脈絡的開頭或結尾時。
- 如果形成回覆的相關資訊位於內容中間,則相對較低。
這個詞彙出自「Lost in the Middle: How Language Models Use Long Contexts」。
低秩適應 (LoRA)
這項參數高效微調技術會「凍結」模型的預先訓練權重 (使其無法再修改),然後在模型中插入一小組可訓練的權重。這組可訓練的權重 (也稱為「更新矩陣」) 比基礎模型小得多,因此訓練速度快得多。
LoRA 具有下列優點:
- 提升模型在套用微調的領域中進行預測的品質。
- 相較於需要微調模型「所有」參數的技術,微調速度更快。
- 啟用多個共用相同基礎模型的專業模型,同時提供服務,藉此降低推論的運算成本。
LSTM
長短期記憶的縮寫。
M
機器學習
根據輸入資料訓練模型的程式或系統。訓練好的模型能根據全新或未知資料進行實用預測,這些資料的分布情形與訓練模型時使用的資料相同。
機器學習也指涉與這些程式或系統相關的研究領域。
詳情請參閱「機器學習簡介」課程。
機器翻譯
使用軟體 (通常是機器學習模型) 將文字從一種人類語言轉換為另一種人類語言,例如從英文轉換為日文。
多數類別
類別不平衡資料集中較常見的標籤。舉例來說,如果資料集中有 99% 的負面標籤和 1% 的正面標籤,負面標籤就是多數類別。
與少數類別形成對比。
詳情請參閱機器學習速成課程中的「資料集:不平衡的資料集」。
馬可夫決策程序 (MDP)
決策模型圖,代表在馬可夫性質成立的假設下,為導覽一連串狀態而採取的決策 (或動作)。在增強式學習中,狀態之間的這些轉換會傳回數值獎勵。
馬可夫屬性
某些環境的屬性,其中狀態轉換完全取決於目前狀態和代理程式動作中隱含的資訊。
遮罩語言模型
語言模型:預測候選符記填入序列空白處的機率。舉例來說,遮罩語言模型可以計算候選字詞的機率,以取代下列句子中的底線:
The ____ in the hat came back.
文獻通常會使用「MASK」字串,而不是底線。 例如:
帽子上的「MASK」字樣又回來了。
大多數現代遮罩語言模型都是雙向。
matplotlib
開放原始碼 Python 2D 繪圖程式庫。matplotlib 可協助您將機器學習的不同面向視覺化。
矩陣分解
在數學中,這是一種機制,可找出點積近似於目標矩陣的矩陣。
在推薦系統中,目標矩陣通常會保留使用者對項目的評分。舉例來說,電影推薦系統的目標矩陣可能如下所示,其中正整數是使用者評分,0 表示使用者未評分:
| 卡薩布蘭加 | 費城故事 | 黑豹 | 神力女超人 | 黑色追緝令 | |
|---|---|---|---|---|---|
| 使用者 1 | 5.0 | 3.0 | 0.0 | 2.0 | 0.0 |
| 使用者 2 | 4.0 | 0.0 | 0.0 | 1.0 | 5.0 |
| 使用者 3 | 3.0 | 1.0 | 4.0 | 5.0 | 0.0 |
電影推薦系統的目標是預測使用者對未評分電影的評分。舉例來說,使用者 1 會喜歡《黑豹》嗎?
建議系統的一種做法是使用矩陣分解,產生下列兩個矩陣:
舉例來說,對三位使用者和五項商品執行矩陣分解,可能會產生下列使用者矩陣和商品矩陣:
User Matrix Item Matrix 1.1 2.3 0.9 0.2 1.4 2.0 1.2 0.6 2.0 1.7 1.2 1.2 -0.1 2.1 2.5 0.5
使用者矩陣和項目矩陣的點積會產生建議矩陣,其中不僅包含原始使用者評分,也包含每位使用者未看過電影的預測結果。舉例來說,假設使用者 1 給予《北非諜影》5.0 分,建議矩陣中對應於該儲存格的點積應接近 5.0,而實際值為:
(1.1 * 0.9) + (2.3 * 1.7) = 4.9更重要的是,使用者 1 會喜歡《黑豹》嗎?將第一列和第三欄對應的點積相乘,即可得出預測評分 4.3:
(1.1 * 1.4) + (2.3 * 1.2) = 4.3矩陣分解通常會產生使用者矩陣和項目矩陣,兩者加總起來比目標矩陣精簡許多。
平均絕對誤差 (MAE)
使用 L1 損失時,每個樣本的平均損失。平均絕對誤差的計算方式如下:
- 計算批次的 L1 損失。
- 將 L1 損失除以批次中的樣本數。
舉例來說,請考慮下列五個範例批次的 L1 損失計算:
| 範例的實際值 | 模型預測值 | 損失 (實際值與預測值之間的差異) |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L1 損失 | ||
因此,L1 損失為 8,範例數為 5。因此,平均絕對誤差為:
Mean Absolute Error = L1 loss / Number of Examples Mean Absolute Error = 8/5 = 1.6
前 k 項的平均精確度平均值 (mAP@k)
驗證資料集中所有「k 處的平均精確度」分數的統計平均值。在 k 處使用平均精確度,可判斷推薦系統產生的建議品質。
雖然「平均值」一詞聽起來有些多餘,但這個指標名稱很合適。畢竟這項指標會找出多個「k 處的平均精確度」值的平均值。
均方誤差 (MSE)
使用 L2 損失時,每個樣本的平均損失。均方誤差的計算方式如下:
- 計算批次的 L2 損失。
- 將 L2 損失除以批次中的樣本數。
舉例來說,請看下列五個樣本批次的損失:
| 實際值 | 模型預測 | 損失 | 平方損失 |
|---|---|---|---|
| 7 | 6 | 1 | 1 |
| 5 | 4 | 1 | 1 |
| 8 | 11 | 3 | 9 |
| 4 | 6 | 2 | 4 |
| 9 | 8 | 1 | 1 |
| 16 = L2 損失 | |||
因此,均方誤差為:
Mean Squared Error = L2 loss / Number of Examples Mean Squared Error = 16/5 = 3.2
TensorFlow Playground 會使用均方差計算損失值。
網格
在機器學習平行程式設計中,這個詞彙與將資料和模型指派給 TPU 晶片,以及定義這些值如何分片或複製有關。
「網格」一詞有多種含意,可能指下列任一項目:
- TPU 晶片的實體配置。
- 抽象邏輯建構體,用於將資料和模型對應至 TPU 晶片。
無論是哪種情況,網格都會指定為形狀。
元學習
機器學習的子集,可探索或改良學習演算法。 元學習系統的目標也可以是訓練模型,以便從少量資料或先前工作獲得的經驗中,快速學習新工作。元學習演算法通常會嘗試達成下列目標:
- 改善或學習手動設計的特徵 (例如初始值設定器或最佳化工具)。
- 更有效率地運用資料和運算資源。
- 改善一般化功能。
元學習與少量樣本學習相關。
指標
您重視的統計資料。
目標是機器學習系統嘗試最佳化的指標。
指標 API (tf.metrics)
用於評估模型的 TensorFlow API。舉例來說,tf.metrics.accuracy 可判斷模型的預測結果與標籤相符的頻率。
小批
在一次疊代中處理的批次資料中,隨機選取的一小部分子集。迷你批次的批次大小通常介於 10 到 1,000 個樣本之間。
舉例來說,假設整個訓練集 (完整批次) 包含 1,000 個範例。假設您將每個迷你批次的批次大小設為 20。因此,每次疊代都會從 1,000 個範例中隨機選取 20 個,判斷損失,然後據此調整權重和偏差。
計算迷你批次的損失,比計算完整批次中所有範例的損失更有效率。
詳情請參閱機器學習速成課程中的「線性迴歸:超參數」。
小批隨機梯度下降法
使用小批次的梯度下降演算法。換句話說,小批隨機梯度下降法會根據一小部分的訓練資料估算梯度。一般隨機梯度下降法會使用大小為 1 的小批。
minimax loss
生成對抗網路的損失函式,以生成資料和真實資料分布之間的交叉熵為依據。
第一篇論文使用極小極大損失來描述生成對抗網路。
詳情請參閱「生成對抗網路」課程中的損失函式。
少數類別
在類別不平衡的資料集中,較不常見的標籤。舉例來說,假設資料集包含 99% 的負面標籤和 1% 的正面標籤,則正面標籤屬於少數類別。
與多數類別形成對比。
詳情請參閱機器學習速成課程中的「資料集:不平衡的資料集」。
專家混合
這項機制只會使用部分參數 (稱為「專家」) 處理特定輸入權杖或範例,藉此提高類神經網路效率。閘道網路會將每個輸入權杖或範例,傳送給適當的專家。
詳情請參閱下列任一論文:
ML
機器學習的縮寫。
MMIT
多模態指令調整的縮寫。
MNIST
由 LeCun、Cortes 和 Burges 彙整的公有領域資料集,內含 60,000 張圖片,每張圖片都顯示人類手動寫下特定數字 (0 到 9) 的方式。每張圖片都會儲存為 28x28 的整數陣列,其中每個整數都是介於 0 到 255 之間的灰階值 (含首尾)。
MNIST 是機器學習的標準資料集,通常用於測試新的機器學習做法。詳情請參閱「 手寫數字的 MNIST 資料庫」。
模態
高階資料類別。舉例來說,數字、文字、圖片、影片和音訊是五種不同的模態。
模型
一般來說,任何可處理輸入資料並傳回輸出內容的數學建構體,換句話說,模型是系統進行預測時所需的一組參數和結構。在監督式機器學習中,模型會將範例做為輸入內容,並推斷預測結果做為輸出內容。在監督式機器學習中,模型會有些許差異。例如:
您可以儲存、還原或複製模型。
非監督式機器學習也會產生模型,通常是可將輸入範例對應至最合適叢集的函式。
模型容量
模型可學習的問題複雜程度。模型能學習的問題越複雜,模型的能力就越高。模型容量通常會隨著模型參數數量增加。如要瞭解分類模型容量的正式定義,請參閱「VC 維度」。
模型串聯
系統會為特定推論查詢挑選理想的模型。
假設有一組模型,從非常大 (大量參數) 到小得多 (參數少得多) 都有。與較小的模型相比,超大型模型在推論時會消耗更多運算資源。不過,大型模型通常能推斷出比小型模型更複雜的要求。模型串聯會判斷推論查詢的複雜程度,然後選擇合適的模型執行推論。模型串聯的主要動機是選取較小的模型,並只針對較複雜的查詢選取較大的模型,藉此降低推論成本。
假設手機上執行的是小型模型,而遠端伺服器上執行的是該模型較大的版本。良好的模型串聯可讓較小的模型處理簡單要求,並只呼叫遠端模型處理複雜要求,進而降低成本和延遲時間。
另請參閱模型路由器。
模型平行處理
一種訓練或推論的擴充方式,可將一個模型的不同部分放在不同的裝置上。模型平行化可讓模型在單一裝置上執行,即使模型過大也沒問題。
如要實作模型平行化,系統通常會執行下列操作:
- 將模型分割成較小的部分。
- 將這些較小部分的訓練作業分配到多個處理器。 每個處理器都會訓練模型的一部分。
- 合併結果以建立單一模型。
模型平行處理會減緩訓練速度。
另請參閱資料平行處理。
模型路由器
這個演算法會決定 模型串聯中推論的理想模型。模型路由器本身通常是機器學習模型,會逐步學習如何為特定輸入內容挑選最佳模型。不過,模型路由器有時可能是較簡單的非機器學習演算法。
模型訓練
判斷最佳模型的過程。
MOE
專家混合的縮寫。
累積熱度
這是一種進階的梯度下降演算法,學習步驟不僅取決於目前步驟的導數,也取決於前一個或多個步驟的導數。動量涉及計算一段時間內梯度指數加權移動平均值,類似於物理學中的動量。動量有時可避免學習過程停滯在局部最小值。
MT
機器翻譯的縮寫。
多元分類
在監督式學習中,資料集包含兩個以上的標籤類別,就是分類問題。舉例來說,Iris 資料集中的標籤必須是下列三種類別之一:
- 剛毛鳶尾
- Iris virginica
- 變色鳶尾
以 Iris 資料集訓練的模型可預測新樣本的 Iris 類型,這就是多元分類。
相反地,如果分類問題要區分兩個類別,則為二元分類模型。舉例來說,如果電子郵件模型預測結果為「垃圾郵件」或「非垃圾郵件」,就是二元分類模型。
在叢集問題中,多元分類是指兩個以上的叢集。
詳情請參閱機器學習速成課程中的「類神經網路:多類別分類」。
多重類別邏輯迴歸
多頭自注意力
自注意力的擴充功能,會針對輸入序列中的每個位置,多次套用自注意力機制。
Transformer 導入了多頭自注意力機制。
多模態指令微調
經過指令微調的模型,可處理文字以外的輸入內容,例如圖片、影片和音訊。
多模態模型
輸入、輸出或兩者包含多種「模態」的模型。舉例來說,假設模型會將圖片和文字說明 (兩種模態) 做為特徵,並輸出分數,指出文字說明是否適合圖片。因此,這個模型的輸入內容是多模態,輸出內容則是單模態。
多元分類
與多元分類同義。
多元迴歸
多重類別邏輯迴歸的同義詞。
多工
多工作模型是透過適合各項不同工作的資料訓練而成。模型可藉此學會在各項工作之間分享資訊,進而更有效率地學習。
經過多項任務訓練的模型通常具有更強大的泛化能力,且能更穩健地處理不同類型的資料。
否
Nano
相對較小的 Gemini 模型,專為裝置端使用而設計。詳情請參閱「Gemini Nano」。
NaN 陷阱
當模型中的某個數字在訓練期間變成 NaN 時,模型中許多或所有其他數字最終都會變成 NaN。
NaN 是「Not a Number」(非數字) 的縮寫。
自然語言處理
這個領域的目標是教導電腦使用語言規則,處理使用者說出或輸入的內容。幾乎所有現代自然語言處理技術都仰賴機器學習。自然語言理解
自然語言處理的子集,可判斷說話或輸入內容的意圖。自然語言理解技術可超越自然語言處理,考量語言的複雜層面,例如脈絡、諷刺和情緒。
負類
在二元分類中,一個類別稱為「正向」,另一個類別稱為「負向」。正類是模型測試的項目或事件,負類則是其他可能性。例如:
- 醫療檢測的負面類別可能是「非腫瘤」。
- 在電子郵件分類模型中,負面類別可能是「非垃圾內容」。
與正類形成對比。
負例取樣
與候選抽樣同義。
神經架構搜尋 (NAS)
自動設計類神經網路架構的技術。NAS 演算法可減少訓練神經網路所需的時間和資源。
NAS 通常會使用:
- 搜尋空間,也就是一組可能的架構。
- 適應度函式,用於衡量特定架構在指定工作上的成效。
NAS 演算法通常會從一小組可能的架構開始,並隨著演算法進一步瞭解哪些架構有效,逐步擴大搜尋空間。適應度函式通常以架構在訓練集上的效能為準,而演算法通常是使用強化學習技術訓練而成。
NAS 演算法已證明能有效找出各種工作的高效能架構,包括圖像分類、文字分類和機器翻譯。
輸出內容
至少包含一個隱藏層的模型。深層類神經網路是一種類神經網路,含有多個隱藏層。舉例來說,下圖顯示包含兩個隱藏層的深層類神經網路。
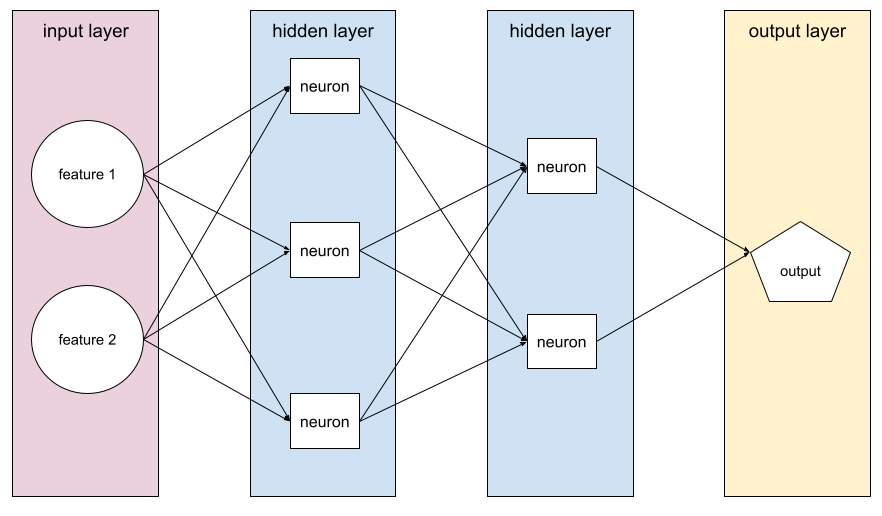
類神經網路中的每個神經元都會連結至下一層的所有節點。舉例來說,在上圖中,請注意第一個隱藏層中的三個神經元,分別連線至第二個隱藏層中的兩個神經元。
在電腦上實作的類神經網路有時稱為「人工類神經網路」,以區別於大腦和其他神經系統中的類神經網路。
部分類神經網路可以模擬不同特徵與標籤之間極為複雜的非線性關係。
詳情請參閱機器學習速成課程中的類神經網路。
神經元
在機器學習中,類神經網路隱藏層中的獨立單元。每個神經元會執行下列兩步驟動作:
第一個隱藏層中的神經元會接受輸入層中的特徵值輸入。第一個隱藏層之後的任何隱藏層神經元,都會接受前一個隱藏層神經元的輸入內容。舉例來說,第二個隱藏層中的神經元會接受第一個隱藏層中神經元的輸入內容。
下圖標示出兩個神經元及其輸入內容。
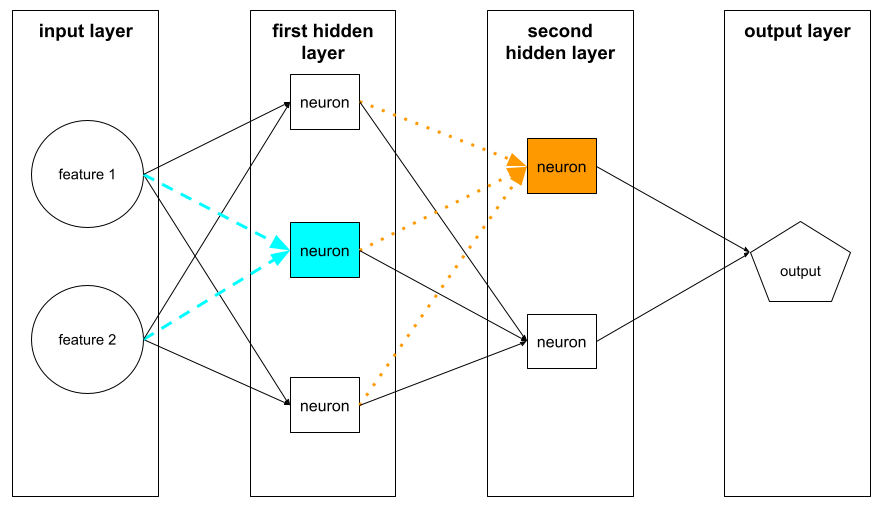
類神經網路中的神經元會模擬大腦和其他神經系統部位的神經元行為。
N 元語法
N 個字詞的排序序列。舉例來說,「truly madly」是 2-gram。由於順序很重要,因此「madly truly」與「truly madly」是不同的 2-gram。
| 否 | 這類 N 元語的名稱 | 範例 |
|---|---|---|
| 2 | 雙連詞或 2 連詞 | to go、go to、eat lunch、eat dinner |
| 3 | 三元或 3 元 | 吃太多、從此過著幸福快樂的日子、喪鐘響起 |
| 4 | 4 公克 | walk in the park, dust in the wind, the boy ate lentils |
許多自然語言理解模型會根據 N 元語法,預測使用者接下來會輸入或說出哪個字詞。舉例來說,假設使用者輸入「happily ever」。以三元組為基礎的 NLU 模型可能會預測使用者接下來會輸入「after」這個字。
與詞袋 (無序的字詞集合) 形成對比。
詳情請參閱機器學習速成課程中的大型語言模型。
自然語言處理
自然語言處理的縮寫。
自然語言理解
自然語言理解的縮寫。
節點 (決策樹)

詳情請參閱決策樹林課程中的決策樹。
節點 (類神經網路)
詳情請參閱機器學習速成課程中的類神經網路。
節點 (TensorFlow 圖表)
TensorFlow 圖形中的運算。
噪音
廣義來說,任何會遮蓋資料集信號的內容。資料可能會因為各種原因而出現雜訊。例如:
- 人工評估人員在標記時出錯。
- 人為或儀器記錄錯誤或遺漏特徵值。
非二元條件
條件包含兩種以上的可能結果。舉例來說,下列非二元條件包含三種可能結果:
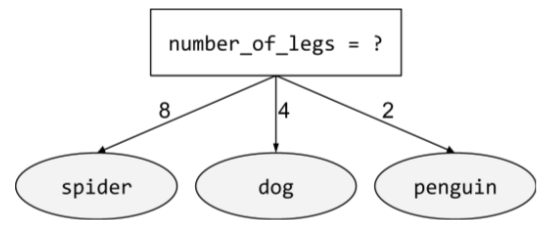
詳情請參閱「決策樹林」課程中的「條件類型」。
非線性
兩個或多個變數之間的關係,無法單純透過加法和乘法表示。線性關係可以表示為一條線,非線性關係則無法。舉例來說,假設有兩個模型,分別將單一特徵與單一標籤建立關聯。左側模型為線性,右側模型為非線性:

如要試用各種非線性函式,請參閱機器學習速成課程中的「類神經網路:節點和隱藏層」。
無反應偏誤
請參閱選擇偏誤。
非平穩性
值會在一或多個維度 (通常是時間) 之間變更的特徵。舉例來說,請參考下列非平穩性範例:
- 特定商店的泳衣銷售量會因季節而異。
- 特定區域在一年中的大部分時間,某種水果的收成量為零,但短時間內收成量很大。
- 由於氣候變遷,年平均溫度正在轉移。
與平穩性形成對比。
沒有唯一正確的答案 (NORA)
講個關於大象的有趣笑話。
評估「沒有正確答案」提示的回覆,通常比評估「只有一個正確答案」提示的回覆更主觀。舉例來說,評估大象笑話需要有系統性的方法,判斷笑話有多好笑。
NORA
沒有哪種格式一定比較好的縮寫。
正規化
廣義來說,將變數的實際值範圍轉換為標準值範圍的過程,例如:
- -1 至 +1
- 0 至 1
- Z 分數 (約 -3 至 +3)
舉例來說,假設某個特徵的實際值範圍是 800 到 2,400,在特徵工程中,您可以將實際值正規化為標準範圍,例如 -1 到 +1。
在特徵工程中,正規化是常見的工作。如果特徵向量中的每個數值特徵範圍大致相同,模型通常會訓練得更快 (並產生更準確的預測)。
另請參閱Z 分數正規化。
詳情請參閱機器學習速成課程中的「數值資料:正規化」。
Notebook LM
這項工具以 Gemini 為基礎,可讓使用者上傳文件,然後使用提示詢問、摘要或整理這些文件。舉例來說,作者可以上傳多篇短篇故事,並要求 NotebookLM 找出共同主題,或判斷哪一篇最適合改編成電影。
新穎性偵測
判斷新 (新穎) 樣本是否與訓練集來自相同分布的過程。換句話說,在訓練集上訓練後,新奇偵測會判斷新樣本 (在推論或額外訓練期間) 是否為離群值。
與離群值偵測形成對比。
數值資料
以整數或實數表示的特徵。舉例來說,房屋估價模型可能會將房屋大小 (以平方英尺或平方公尺為單位) 表示為數值資料。將特徵表示為數值資料,表示特徵值與標籤之間存在數學關係。也就是說,房屋的平方公尺數可能與房屋價值存在某種數學關係。
並非所有整數資料都應以數值資料表示。舉例來說,世界某些地區的郵遞區號是整數,但整數郵遞區號不應以模型中的數值資料表示。這是因為郵遞區號 20000 的效力並非郵遞區號 10000 的兩倍 (或一半)。此外,雖然不同郵遞區號確實與不同的房地產價值相關,但我們無法假設郵遞區號 20000 的房地產價值是郵遞區號 10000 的兩倍。郵遞區號應改為以類別資料表示。
詳情請參閱機器學習速成課程的「處理數值資料」。
NumPy
開放原始碼數學程式庫,可在 Python 中提供有效率的陣列運算。pandas 是以 NumPy 為基礎建構而成。
O
目標
演算法嘗試最佳化的指標。
目標函式
模型要盡量提升的數學公式或指標。 舉例來說,線性迴歸的目標函式通常是均方損失。因此,訓練線性迴歸模型時,訓練目標是盡量減少均方損失。
在某些情況下,目標是盡量提高目標函式。舉例來說,如果目標函式是準確度,目標就是盡可能提高準確度。
另請參閱「損失」。
斜向條件
在決策樹中,條件涉及多個特徵。舉例來說,如果高度和寬度都是特徵,則以下是斜交條件:
height > width
與軸對齊條件形成對比。
詳情請參閱「決策樹林」課程中的「條件類型」。
離線
static 的同義詞。
離線推論
模型產生一批預測結果,然後快取 (儲存) 這些預測結果的過程。應用程式接著可以從快取存取推斷的預測結果,而不必重新執行模型。
舉例來說,假設模型每四小時會產生一次當地天氣預報 (預測)。每次執行模型後,系統都會快取所有當地天氣預報。天氣應用程式會從快取擷取預報。
離線推論也稱為「靜態推論」。
與線上推論形成對比。 詳情請參閱機器學習密集課程的「正式版 ML 系統:靜態與動態推論」。
one-hot 編碼
將類別資料表示為向量,其中:
- 其中一個元素設為 1。
- 所有其他元素都設為 0。
One-hot 編碼通常用於表示具有有限可能值的字串或 ID。舉例來說,假設名為 Scandinavia 的特定類別特徵有五個可能值:
- 「丹麥」
- 「瑞典」
- 「挪威」
- 「芬蘭」
- 「冰島」
One-hot 編碼可將這五個值分別表示如下:
| 國家/地區 | 向量 | ||||
|---|---|---|---|---|---|
| 「丹麥」 | 1 | 0 | 0 | 0 | 0 |
| 「瑞典」 | 0 | 1 | 0 | 0 | 0 |
| 「挪威」 | 0 | 0 | 1 | 0 | 0 |
| 「芬蘭」 | 0 | 0 | 0 | 1 | 0 |
| 「冰島」 | 0 | 0 | 0 | 0 | 1 |
由於採用獨熱編碼,模型可以根據這五個國家/地區的資料,學習不同的連結。
將特徵表示為數值資料是 one-hot 編碼的替代做法。很抱歉,以數字代表斯堪地那維亞國家/地區並非好選擇。舉例來說,請參考下列數字表示法:
- 「丹麥」為 0
- 「瑞典」為 1
- 「挪威」為 2
- 「芬蘭」是 3
- 「冰島」是 4
如果使用數值編碼,模型會以數學方式解讀原始數字,並嘗試根據這些數字進行訓練。但冰島的某項事物並非挪威的兩倍 (或一半),因此模型會得出一些奇怪的結論。
詳情請參閱機器學習速成課程中的「類別資料:詞彙和獨熱編碼」。
一個正確答案 (ORA)
是非題:土星比火星大。
唯一正確的答案是 true。
與「沒有哪種格式一定比較好」形成對比。
單樣本學習
機器學習方法通常用於物件分類,旨在從單一訓練範例中學習有效的分類模型。
單樣本提示
包含一個範例的提示,說明大型語言模型應如何回應。舉例來說,下列提示包含一個範例,向大型語言模型說明如何回答查詢。
| 提示的組成部分 | 附註 |
|---|---|
| 指定國家/地區的官方貨幣為何? | 您希望 LLM 回答的問題。 |
| 法國:歐元 | 舉例來說。 |
| 印度: | 實際查詢。 |
比較單次提示與下列詞彙的異同:
一對多分類法
假設分類問題有 N 個類別,解決方案會包含 N 個獨立的二元分類模型,每個可能的結果都有一個二元分類模型。舉例來說,假設模型會將樣本分類為動物、植物或礦物,一對多解決方案會提供下列三個獨立的二元分類模型:
- 動物與非動物
- 蔬菜與非蔬菜
- 礦物與非礦物
線上
與 dynamic 語法相同。
線上推論
依需求生成預測。舉例來說,假設應用程式將輸入內容傳遞至模型,並發出預測要求。使用線上推論的系統會執行模型,然後將預測結果傳回應用程式,以回應要求。
與離線推論形成對比。
詳情請參閱機器學習密集課程的「正式版 ML 系統:靜態與動態推論」。
作業 (op)
在 TensorFlow 中,凡是建立、操控或毀損 Tensor 的程序,舉例來說,矩陣相乘作業會將兩個張量做為輸入,並產生一個張量做為輸出。
Optax
適用於 JAX 的梯度處理和最佳化程式庫。 Optax 提供可自訂重組的建構區塊,有助於研究人員最佳化深層類神經網路等參數模型。其他目標包括:
- 提供可讀、經過充分測試且有效率的核心元件實作項目。
- 可將低階成分組合成自訂最佳化工具 (或其他梯度處理元件),進而提高生產力。
- 讓任何人都能輕鬆貢獻,加快採用新想法的腳步。
最佳化工具
梯度下降演算法的特定實作方式。熱門最佳化器包括:
- AdaGrad,是「自適應梯度下降」的簡稱。
- Adam,代表「ADAptive with Momentum」(適應性動量)。
ORA
一個正確答案的縮寫。
外團體同質性偏誤
與同類群體成員相比,傾向認為異類群體成員更為相似,並比較態度、價值觀、人格特質和其他特徵。群內是指經常互動的對象;群外是指不常互動的對象。如果您要求使用者提供外部群組的屬性,這些屬性可能比參與者列出的內部群組屬性更缺乏細微差異,也更刻板印象。
舉例來說,小人國人可能會詳細描述其他小人國人的房屋,並指出建築風格、窗戶、門和大小的細微差異。然而,小人國人可能只是宣稱巨人國人全都住在相同的房子裡。
外團體同質性偏誤是團體歸因偏誤的一種形式。
另請參閱內團體偏誤。
離群值偵測
與新穎性偵測形成對比。
成效突出的影片
與大多數其他值相差甚遠的值。在機器學習中,下列任一項目都屬於離群值:
- 輸入值與平均值相差超過約 3 個標準差的資料。
- 權重的絕對值較高。
- 預測值與實際值相差甚遠。
舉例來說,假設 widget-price 是特定模型的特徵。
假設平均值 widget-price 為 7 歐元,標準差為 1 歐元。因此,widget-price 為 12 歐元或 2 歐元的例子會被視為離群值,因為這些價格與平均值相差五個標準差。
離群值通常是因輸入錯誤或筆誤所致。在其他情況下,離群值並非錯誤;畢竟,與平均值相差五個標準差的值雖然罕見,但並非不可能。
離群值通常會導致模型訓練發生問題。裁剪是管理離群值的其中一種方式。
詳情請參閱機器學習速成課程的「處理數值資料」。
袋外評估 (OOB 評估)
評估決策樹林品質的機制,方法是針對範例測試每個決策樹,這些範例不會用於該決策樹的訓練。舉例來說,在下圖中,系統會針對約三分之二的樣本訓練每個決策樹,然後根據其餘三分之一的樣本進行評估。
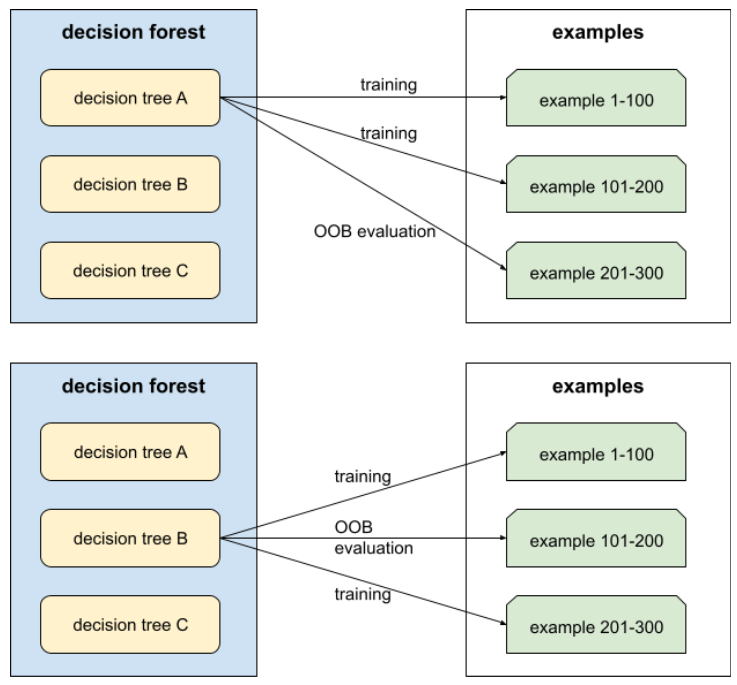
袋外評估是交叉驗證機制,可有效率地估算保守值。在交叉驗證中,每個交叉驗證回合都會訓練一個模型 (例如,在 10 折交叉驗證中,會訓練 10 個模型)。使用 OOB 評估時,系統會訓練單一模型。由於裝袋會在訓練期間保留每棵樹的部分資料,因此 OOB 評估可使用這些資料來近似交叉驗證。
詳情請參閱決策樹林課程中的袋外評估。
輸出層
類神經網路的「最終」層。輸出層包含預測結果。
下圖顯示一個小型深層類神經網路,包含輸入層、兩個隱藏層和輸出層:
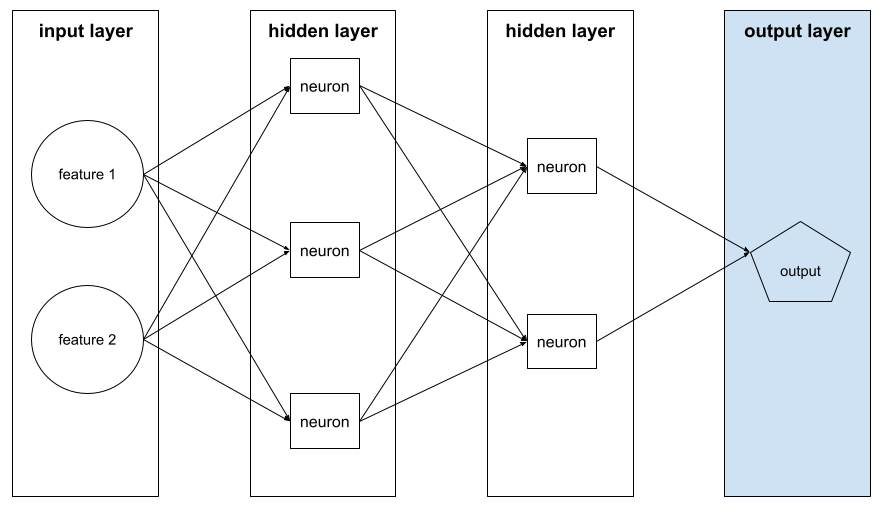
過度配適
建立與訓練資料過於相符的模型,導致模型無法對新資料做出正確預測。
正則化可減少過度配適的情況。 以大型且多元的訓練集進行訓練,也能減少過度配適。
詳情請參閱機器學習速成課程中的「過度擬合」。
過度取樣
在類別不平衡的資料集中,重複使用少數類別的範例,建立更平衡的訓練集。
舉例來說,假設某個二元分類問題中,多數類別與少數類別的比例為 5,000:1。如果資料集包含一百萬個範例,則少數類別的範例只約有 200 個,這可能不足以有效訓練模型。為克服這項缺點,您可能會多次過度取樣 (重複使用) 這 200 個範例,或許能產生足夠的範例,以利訓練。
過度取樣時,請務必小心過度擬合。
與欠採樣形成對比。
P
封裝資料
更有效率的資料儲存方式。
封裝資料會使用壓縮格式或其他方式儲存資料,以便更有效率地存取資料。封裝資料可將存取資料所需的記憶體和運算量降至最低,進而加快訓練速度,並提升模型推論效率。
打包資料通常會搭配其他技術 (例如資料擴增和正則化) 使用,進一步提升模型的效能。
PaLM
pandas
以 numpy 為基礎建構的欄導向資料分析 API。許多機器學習架構 (包括 TensorFlow) 都支援將 pandas 資料結構做為輸入內容。詳情請參閱 pandas 說明文件。
參數
模型在訓練期間學到的權重和偏誤。舉例來說,在線性迴歸模型中,參數包含下列公式中的偏差 (b) 和所有權重 (w1、w2 等等):
相較之下,超參數是您 (或超參數微調服務) 提供給模型的值。舉例來說,學習率就是超參數。
高效參數調整
這是一組技術,可比完整微調更有效率地微調大型預先訓練語言模型 (PLM)。與完整微調相比,高效參數微調通常微調的參數少得多,但一般來說,產生的大型語言模型效能與完整微調建立的大型語言模型相同 (或幾乎相同)。
比較具參數運用效率的調整機制與下列項目:
高效參數調整也稱為「高效參數微調」。
參數伺服器 (PS)
這項工作會在分散式環境中追蹤模型的參數。
參數更新
在訓練期間調整模型參數的作業,通常是在單一疊代梯度下降中進行。
偏導數
其中一個變數以外的所有變數都視為常數的衍生值。 舉例來說,f(x, y) 對 x 的偏導數,就是將 f 視為僅以 x 為變數的函式 (也就是將 y 視為常數) 所得的導數。f 對 x 的偏導數只著重於 x 的變化,並忽略方程式中的所有其他變數。
參與偏誤
無反應偏誤的同義詞。請參閱選擇偏誤。
分區策略
將變數分配到參數伺服器的演算法。
pass at k (pass@k)
這項指標可判斷大型語言模型生成的程式碼 (例如 Python) 品質。具體來說,k 代表在 k 個生成的程式碼區塊中,至少有一個程式碼區塊通過所有單元測試的機率。
大型語言模型通常難以針對複雜的程式設計問題生成優質程式碼。軟體工程師會適應這個問題,提示大型語言模型為同一問題生成多個 (k) 解決方案。接著,軟體工程師會針對單元測試,測試每項解決方案。k 的通過計算取決於單元測試的結果:
- 如果一或多個解決方案通過單元測試,LLM 就通過該程式碼生成挑戰。
- 如果沒有任何解決方案通過單元測試,LLM 就無法通過程式碼生成挑戰。
k 的傳遞公式如下:
\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]
一般而言,k 值越高,通過 k 分數就越高;不過,k 值越高,需要的大型語言模型和單元測試資源就越多。
Pathways 語言模型 (PaLM)
是 Gemini 模型的前身,也是較舊的模型。
Pax
程式設計架構,專為訓練大規模類神經網路 模型而設計,模型規模龐大,可跨越多個 TPU 加速器晶片 切片或 Pod。
Pax 是以 Flax 為基礎建構,而 Flax 則是以 JAX 為基礎建構。
感知器
系統 (硬體或軟體) 會接收一或多個輸入值,對輸入值的加權總和執行函式,並計算單一輸出值。在機器學習中,這類函式通常為非線性,例如 ReLU、sigmoid 或 tanh。舉例來說,下列感知器會依賴 Sigmoid 函式處理三個輸入值:
在下圖中,感知器會接收三項輸入內容,每項內容都會先經過權重修改,再輸入感知器:

performance
多重意義的字詞:
- 軟體工程中的標準意義。也就是:這段軟體執行的速度 (或效率) 有多快?
- 機器學習中的意義。這裡的「成效」會回答下列問題:這個模型有多正確?也就是說,模型的預測結果有多準確?
排序變數重要性
一種變數重要性,用於評估模型在特徵值經過排列後,預測錯誤率的增幅。排序變數重要性是與模型無關的指標。
困惑度
用來評估模型完成工作的程度。舉例來說,假設您的工作是讀取使用者在手機鍵盤上輸入的字詞前幾個字母,並提供可能的完成字詞清單。這項工作的困惑度 P 大約是您需要提供的猜測次數,才能讓清單包含使用者嘗試輸入的實際字詞。
困惑度與交叉熵的關係如下:
pipeline
機器學習演算法周圍的基礎架構。管道包括收集資料、將資料放入訓練資料檔案、訓練一或多個模型,以及將模型匯出至正式環境。
詳情請參閱「管理機器學習專案」課程中的機器學習管道。
管道化
一種模型平行化形式,模型處理作業會分成連續階段,每個階段都在不同裝置上執行。當某個階段處理一個批次時,前一個階段可以處理下一個批次。
另請參閱階段式訓練。
pjit
JAX 函式,可將程式碼分割,在多個加速器晶片上執行。使用者會將函式傳遞至 pjit,而 pjit 會傳回具有同等語意的函式,但會編譯成在多個裝置 (例如 GPU 或 TPU 核心) 上執行的 XLA 運算。
使用者可以透過 pjit,使用 SPMD 分區器,將運算作業分片,不必重新編寫。
自 2023 年 3 月起,pjit 已併入 jit。詳情請參閱「分散式陣列和自動平行化」。
PLM
預先訓練語言模型的縮寫。
pmap
JAX 函式,可在多個基礎硬體裝置 (CPU、GPU 或 TPU) 上執行輸入函式的副本,並使用不同的輸入值。pmap 依賴 SPMD。
政策
彙整
將先前卷積層建立的矩陣縮減為較小的矩陣。匯總通常會取匯總區域的最大值或平均值。舉例來說,假設我們有下列 3x3 矩陣:
![3x3 矩陣 [[5,3,1], [8,2,5], [9,4,3]]。](https://developers.google.com/static/machine-learning/glossary/images/PoolingStart.svg?authuser=1&hl=zh-tw)
與卷積運算一樣,集區運算會將矩陣分割成切片,然後以步幅滑動卷積運算。舉例來說,假設集區化作業將捲積矩陣劃分為 2x2 的切片,步幅為 1x1。如下圖所示,會進行四項集區作業。假設每個集區作業都會選取該切片中四個值的最大值:
![輸入矩陣為 3x3,值為:[[5,3,1], [8,2,5], [9,4,3]]。
輸入矩陣的左上 2x2 子矩陣為 [[5,3], [8,2]],因此左上池化作業會產生值 8 (這是 5、3、8 和 2 的最大值)。輸入矩陣的右上角 2x2 子矩陣為 [[3,1], [2,5]],因此右上角匯總作業會產生值 5。輸入矩陣的左下角 2x2 子矩陣為 [[8,2], [9,4]],因此左下角集區化作業會產生值 9。輸入矩陣的右下 2x2 子矩陣為 [[2,5], [4,3]],因此右下集區化作業會產生值 5。總而言之,集區運算會產生 2x2 矩陣 [[8,5], [9,5]]。](https://developers.google.com/static/machine-learning/glossary/images/PoolingConvolution.svg?authuser=1&hl=zh-tw)
集區化有助於在輸入矩陣中強制執行平移不變性。
視覺應用程式的集區化更正式的名稱是「空間集區化」。時序應用程式通常將集區化稱為「時間集區化」。非正式來說,集區化通常稱為「子取樣」或「下取樣」。
請參閱 ML Practicum:圖片分類課程中的「卷積類神經網路簡介」。
位置編碼
這項技術可將序列中權杖的位置相關資訊新增至權杖的嵌入。Transformer 模型會使用位置編碼,進一步瞭解序列不同部分之間的關係。
位置編碼的常見實作方式是使用正弦函數。(具體來說,正弦函數的頻率和振幅是由序列中符記的位置決定)。這項技術可讓 Transformer 模型根據序列中的位置,學習關注序列的不同部分。
正類
您要測試的類別。
舉例來說,癌症模型中的正向類別可能是「腫瘤」。 電子郵件分類模型中的正類可能是「垃圾郵件」。
與負類形成對比。
後續處理
在模型執行後調整輸出內容。 後續處理可用於強制執行公平性限制,而不必修改模型本身。
舉例來說,您可以設定分類門檻,對二元分類模型套用後續處理,確保某個屬性的機會均等,方法是檢查該屬性所有值的真正陽性率是否相同。
後訓練模型
這個詞彙的定義較為寬鬆,通常是指經過一些後續處理的預先訓練模型,例如:
PR AUC (PR 曲線下面積)
內插精確度與喚回度曲線下的面積,是透過繪製不同分類門檻值的 (喚回度、精確度) 點取得。
Praxis
Pax 的核心高效能機器學習程式庫。Praxis 通常稱為「層級程式庫」。
Praxis 不僅包含 Layer 類別的定義,也包含大部分的支援元件,包括:
Praxis 提供 Model 類別的定義。
精確性
分類模型的指標,可用來回答下列問題:
模型預測正類時,預測正確的百分比是多少?
公式如下:
其中:
- 真陽性是指模型正確預測正類。
- 偽陽性是指模型錯誤預測正類。
舉例來說,假設模型做出 200 項正向預測。在這 200 項正向預測中:
- 其中 150 個是真陽性。
- 其中 50 個是誤判。
在這種情況下:
詳情請參閱機器學習速成課程中的「分類:準確度、喚回率、精確度和相關指標」。
前 k 項的查準率 (precision@k)
用於評估排序 (已排序) 項目清單的指標。 「前 k 項的準確率」是指清單中前 k 個項目中「相關」項目的比例。也就是:
\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]
k 的值必須小於或等於傳回清單的長度。 請注意,傳回清單的長度不屬於計算範圍。
關聯性通常是主觀的,即使是人工評估人員也經常對哪些項目相關意見不合。
比較時段:
精確度與喚回度曲線
預測
模型的輸出內容。例如:
- 二元分類模型的預測結果不是正類就是負類。
- 多元分類模型會預測一個類別。
- 線性迴歸模型的預測結果是數字。
預測偏誤
這個值表示資料集中預測�的平均值與標籤的平均值之間的差距。
請勿與機器學習模型中的偏誤項混淆,也不要與倫理和公平性方面的偏誤混淆。
預測機器學習
任何標準 (「傳統」) 機器學習系統。
「預測型機器學習」一詞沒有正式定義。這個詞彙是用來區分不以生成式 AI 為基礎的機器學習系統類別。
預測同位
公平性指標:檢查特定分類模型的準確率是否對所考量的子群組而言相等。
舉例來說,如果模型預測大學錄取結果時,對小人國人和大人國人的預測精確度相同,就符合國籍的預測同等性。
預測同等價格有時也稱為預測同等價格率。
如要進一步瞭解預測均等性,請參閱「公平性定義說明」(第 3.2.1 節)。
預測價格一致性
預測同位的別名。
預先處理
在資料用於訓練模型前進行處理。前處理可能很簡單,例如從英文文字語料庫中移除英文字典中沒有的字詞,也可能很複雜,例如以盡可能消除與敏感屬性相關聯的屬性方式,重新表示資料點。前處理有助於滿足公平性限制。預先訓練模型
雖然這個詞彙可能指任何訓練過的模型或訓練過的嵌入向量,但預先訓練模型現在通常是指訓練過的大型語言模型,或是其他形式的訓練過的生成式 AI 模型。
訓練前
模型在大型資料集上的初始訓練。部分預先訓練模型是笨拙的巨人,通常必須透過額外訓練來精進。舉例來說,機器學習專家可能會先在大量文字資料集 (例如 Wikipedia 中所有英文網頁) 上,預先訓練大型語言模型。預先訓練完成後,您可以透過下列任一技術進一步調整模型:
先驗信念
開始訓練資料前,您對資料的看法。舉例來說,L2 正則化是根據先前的信念,認為權重應較小,且通常會以零為中心呈常態分布。
Pro
Gemini 模型的參數比 Ultra 少,但比 Nano 多。詳情請參閱「Gemini Pro」。
機率迴歸模型
迴歸模型,不僅會使用每個特徵的權重,還會使用這些權重的不確定性。機率迴歸模型會產生預測結果,以及該預測結果的不確定性。舉例來說,機率迴歸模型可能會產生 325 的預測值,標準差為 12。如要進一步瞭解機率迴歸模型,請參閱 tensorflow.org 上的這個 Colab。
機率密度函式
這個函式會找出資料樣本完全符合特定值的頻率。如果資料集的值是連續的浮點數,就很少會出現完全相符的情況。不過,從值 x 到值 y整合機率密度函式,會產生 x 和 y 之間資料樣本的預期頻率。
舉例來說,假設常態分布的平均值為 200,標準差為 30。如要判斷落在 211.4 到 218.7 範圍內的資料樣本預期頻率,您可以整合常態分布的機率密度函式 (從 211.4 到 218.7)。
提示詞
輸入大型語言模型的任何文字,可讓模型以特定方式運作。提示可以短至片語,也可以任意長 (例如整本小說的內容)。提示可分為多個類別,包括下表所示的類別:
| 提示類別 | 範例 | 附註 |
|---|---|---|
| 問題 | 鴿子能飛多快? | |
| 指示 | 寫一首關於套利的打油詩。 | 要求大型語言模型執行某項動作的提示。 |
| 範例 | 將 Markdown 程式碼轉換為 HTML。例如:
Markdown:* list item HTML:<ul> <li>list item</li> </ul> |
這個範例提示的第一句話是指令。 提示的其餘部分是範例。 |
| 角色 | 向物理學博士說明為何機器學習訓練會使用梯度下降法。 | 句子的第一部分是指令,而「物理學博士」則是角色部分。 |
| 模型可補完的部分輸入內容 | 英國首相住在 | 部分輸入提示詞可以突然結束 (如本例所示), 也可以底線結尾。 |
生成式 AI 模型可以根據提示生成文字、程式碼、圖片、嵌入內容、影片等幾乎任何內容。
提示型學習
特定模型的一項功能,可根據任意文字輸入內容 (提示) 調整行為。在典型的提示式學習範例中,大型語言模型會生成文字來回應提示。舉例來說,假設使用者輸入下列提示:
總結牛頓第三運動定律。
能夠根據提示學習的模型並非經過特別訓練,因此無法回答先前的提示。而是「知道」許多物理學事實、一般語言規則,以及一般實用答案的構成要素。這些知識足以提供 (希望) 有用的答案。額外的人工回饋 (例如「這個答案太複雜了」或「什麼是反應?」) 可讓某些以提示為基礎的學習系統逐步提升答案的實用性。
提示設計
提示工程的同義詞。
提示工程
提示設計是指建立提示,從大型語言模型中提取所需回應的程序。人類會執行提示工程。撰寫結構良好的提示是確保大型語言模型提供實用回覆的關鍵。提示工程取決於許多因素,包括:
提示設計是提示工程的同義詞。
如要進一步瞭解如何撰寫實用提示,請參閱「提示設計簡介」。
提示集
一組用於評估大型語言模型的提示。舉例來說,下圖顯示的提示集包含三則提示:
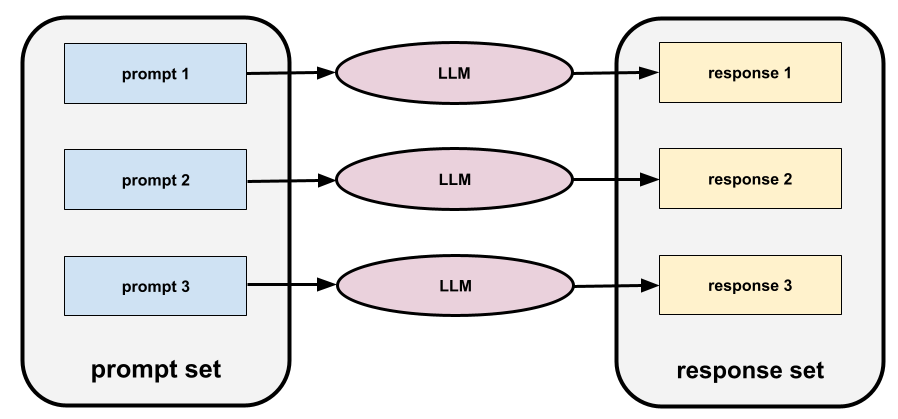
優質的提示集包含足夠「廣泛」的提示,可全面評估大型語言模型的安全性與實用性。
另請參閱「回應集」。
調整提示
參數效率調整機制,可學習系統在實際提示前預先加入的「前置字元」。
提示調整的一種變化形式 (有時稱為「前置字元調整」) 是在每個層級前面加上前置字元。相較之下,大多數的提示調整作業只會將前置字串加到輸入層。
Proxy (敏感屬性)
用來替代私密屬性的屬性。舉例來說,個人的郵遞區號可能用來代表其收入、種族或族裔。代理標籤
資料集中沒有直接提供用於估算標籤的資料。
舉例來說,假設您必須訓練模型來預測員工壓力程度,您的資料集包含許多預測特徵,但沒有名為「壓力程度」的標籤。您不氣餒,選擇「工作場所事故」做為壓力程度的替代標籤。畢竟,壓力大的員工比冷靜的員工更容易發生意外。還是會?或許工作場所事故的發生率會因為多種原因而起伏。
再舉一例,假設您想將「下雨了嗎?」設為資料集的布林標籤,但資料集不含降雨資料。如果有相片,您可以將「有人拿傘」的圖片設為「是否正在下雨?」的替代標籤。這是合適的代理標籤嗎?可能,但某些文化的人可能比較常攜帶雨傘來遮陽,而不是擋雨。
Proxy 標籤通常不完美。請盡可能選擇實際標籤,而非替代標籤。也就是說,如果沒有實際標籤,請非常謹慎地挑選替代標籤,選擇最不糟糕的替代標籤候選項目。
詳情請參閱機器學習密集課程中的「資料集:標籤」。
純函式
輸出結果僅根據輸入內容,且沒有任何副作用的函式。具體來說,純函式不會使用或變更任何全域狀態,例如檔案內容或函式外部變數的值。
您可以使用純函式建立執行緒安全程式碼,在多個加速器晶片之間對 模型程式碼進行分片時,這項功能非常實用。
JAX 的函式轉換方法要求輸入函式為純函式。
Q
Q 函式
在強化學習中,函式會預測在狀態中採取動作,然後遵循特定政策,所產生的預期回報。
Q 函式也稱為狀態動作值函式。
Q 學習
在強化學習中,演算法可讓代理程式套用 Bellman 方程式,藉此瞭解 Markov 決策程序的最佳 Q 函式。馬可夫決策程序會模擬環境。
分位數
分位數分組中的每個 bucket。
分位數分組
將特徵值分配到值區,讓每個值區包含相同 (或幾乎相同) 數量的範例。舉例來說,下圖將 44 點分成 4 個區間,每個區間包含 11 點。為確保圖中的每個值區都包含相同數量的點,部分值區的 x 值範圍寬度會有所不同。

詳情請參閱機器學習速成課程中的「數值資料:分組」。
量化
過度使用的字詞,可能用於下列任一用途:
- 在特定特徵上實作分位數值區化。
- 將資料轉換為 0 和 1,以便更快儲存、訓練及推論。由於布林資料比其他格式更不容易受到雜訊和錯誤影響,量化作業可以提升模型正確性。量化技術包括捨入、截斷和分箱。
減少用於儲存模型參數的位元數。舉例來說,假設模型的參數是以 32 位元浮點數儲存。量化會將這些參數從 32 位元轉換為 4、8 或 16 位元。量化會減少下列項目:
- 運算、記憶體、磁碟和網路用量
- 推斷預測結果所需的時間
- 耗電量
不過,量化有時會降低模型預測的正確性。
佇列
實作佇列資料結構的 TensorFlow Operation。通常用於 I/O。
R
RAG
檢索增強生成的縮寫。
隨機森林
決策樹集合,其中每棵決策樹都會以特定隨機雜訊訓練,例如袋裝。
隨機樹系是決策樹系的一種。
詳情請參閱決策樹課程中的「隨機森林」。
隨機政策
等級 (序數)
機器學習問題中類別的序數位置,可將類別從最高到最低排序。舉例來說,行為排序系統可能會將狗狗的獎勵從最高 (牛排) 到最低 (枯萎的羽衣甘藍) 排序。
秩 (Tensor)
Tensor中的維度數量。舉例來說,純量的等級為 0、向量的等級為 1,而矩陣的等級為 2。
請勿與排名 (序數)混淆。
排名
一種監督式學習,目標是排序項目清單。
評分人員
詳情請參閱機器學習速成課程中的「類別資料:常見問題」。
召回
分類模型的指標,可用來回答下列問題:
公式如下:
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
其中:
- 真陽性是指模型正確預測正類。
- 偽陰性表示模型錯誤預測為負類。
舉例來說,假設模型對基準真相為正類的樣本做出 200 項預測。在這 200 項預測中:
- 其中 180 個是真陽性。
- 其中 20 個是偽陰性。
在這種情況下:
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
詳情請參閱「分類:準確度、查全率、查準率和相關指標」。
k 時的召回率 (recall@k)
這項指標用於評估輸出排序 (依序) 項目清單的系統。「前 k 項的召回率」是指清單中前 k 項的相關項目比例,以傳回的相關項目總數為分母。
\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]
對比度為 k 的精確度。
推薦系統
這類系統會從大量語料庫中,為每位使用者選取相對較少的理想項目。舉例來說,影片推薦系統可能會從 10 萬部影片中推薦兩部影片,為一位使用者選擇《北非諜影》和《費城故事》,為另一位使用者選擇《神力女超人》和《黑豹》。影片推薦系統可能會根據下列因素推薦影片:
- 類似使用者評分或觀看的電影。
- 類型、導演、演員、目標客層...
詳情請參閱推薦系統課程。
線性整流函數 (ReLU)
具有下列行為的啟動函式:
- 如果輸入值為負數或零,輸出值則為 0。
- 如果輸入為正數,輸出會等於輸入。
例如:
- 如果輸入 -3,輸出結果為 0。
- 如果輸入為 +3,則輸出為 3.0。
以下是 ReLU 的繪圖:
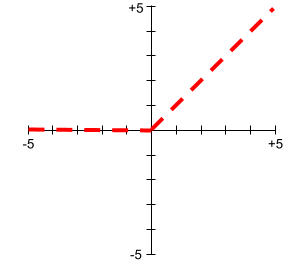
ReLU 是非常熱門的活化函式。雖然 ReLU 的行為很簡單,但仍可讓類神經網路學習非線性關係,也就是特徵與標籤之間的關係。
循環類神經網路
類神經網路會刻意多次執行,每次執行都會將部分結果做為下次執行的輸入內容。具體來說,前一次執行的隱藏層會提供部分輸入內容,供下一次執行的相同隱藏層使用。循環類神經網路特別適合評估序列,因此隱藏層可以從先前對序列較早部分執行的類神經網路中學習。
舉例來說,下圖顯示執行四次的循環神經網路。請注意,第一次執行時隱藏層中學習到的值,會成為第二次執行時相同隱藏層的輸入內容。同樣地,第二次執行時隱藏層中學到的值,會成為第三次執行時相同隱藏層的輸入內容。這樣一來,遞迴神經網路就能逐步訓練並預測整個序列的意義,而不只是個別字詞的意義。

參考文字
專家對提示的回覆。舉例來說,假設您輸入下列提示:
將「What is your name?」這個問題從英文翻譯成法文。
專家可能會回覆:
Comment vous appelez-vous?
各種指標 (例如 ROUGE) 會評估參照文字與 ML 模型生成的文字的相符程度。
反思
這項策略可檢查 (反思) 步驟的輸出內容,再將該輸出內容傳遞至下一個步驟,藉此提升代理工作流程的品質。
審查員通常是生成回覆的LLM (但也有可能是其他 LLM)。生成回覆的 LLM 如何公正評估自己的回覆?「訣竅」是讓 LLM 處於批判性 (反思) 狀態。這個過程類似於作家先以創意的心態撰寫初稿,然後切換到批判的心態進行編輯。
舉例來說,假設某個代理工作流程的第一步是建立咖啡杯的文字。這個步驟的提示可能如下:
你是創意人員,生成適合印在咖啡杯上、長度少於 50 個半形字元的原創幽默文字。
現在,請想像下列反思提示:
你是咖啡愛好者。您覺得先前的回覆有趣嗎?
工作流程接著可能只會將獲得高反思分數的文字傳遞至下一個階段。
迴歸模型
簡單來說,就是產生數值預測結果的模型。(相較之下,分類模型會產生類別預測結果)。舉例來說,下列皆為迴歸模型:
- 預測特定房屋價值 (以歐元計) 的模型,例如 423,000。
- 模型會預測特定樹木的預期壽命 (以年為單位),例如 23.2 年。
- 模型會預測特定城市在未來六小時內的降雨量 (以英吋為單位),例如 0.18。
迴歸模型有兩種常見類型:
並非所有輸出數值預測結果的模型都是迴歸模型。 在某些情況下,數值預測實際上只是類別名稱為數值的分類模型。舉例來說,預測數字郵遞區號的模型是分類模型,而非迴歸模型。
正則化
任何可減少過度擬合的機制。 常見的正規化類型包括:
正規化也可以定義為模型複雜度的懲罰。
詳情請參閱機器學習速成課程中的「過度擬合:模型複雜度」。
正規化率
這個數字會指定訓練期間正規化的相對重要性。提高正規化率可減少過度配適,但可能會降低模型的預測能力。反之,降低或省略正規化率會增加過度擬合。
詳情請參閱機器學習速成課程中的「過度擬合:L2 正規化」。
增強學習 (RL)
這是一系列演算法,可學習最佳政策,目標是在與環境互動時,盡量提高報酬。舉例來說,大多數遊戲的最終獎勵都是勝利。強化學習系統會評估先前遊戲中最終導致獲勝的動作序列,以及最終導致落敗的動作序列,進而成為複雜遊戲的專家。
人類回饋增強學習 (RLHF)
根據人工評估員的意見回饋,提升模型回覆的品質。舉例來說,RLHF 機制可以要求使用者以「👍」或「👎」表情符號評估模型回覆的品質。系統就能根據意見回饋調整日後的回覆。
ReLU
線性整流函數的縮寫。
重播緩衝區
在 DQN 類似演算法中,代理程式使用的記憶體會儲存狀態轉換,以用於經驗重播。
副本
訓練集或模型的副本 (或部分),通常儲存在另一部機器上。舉例來說,系統可以採用下列策略,實作資料平行處理:
- 在多部機器上放置現有模型的副本。
- 將訓練集的不同子集傳送至每個副本。
- 匯總參數更新。
副本也可以參照另一個推論伺服器的副本。增加副本數量可提高系統能同時處理的要求數量,但也會增加放送費用。
通報偏誤
人們撰寫有關動作、結果或屬性的頻率,並不能反映這些動作、結果或屬性在現實世界中的頻率,也不能反映屬性對某類別個人的特徵程度。報告偏差可能會影響機器學習系統學習的資料組成。
舉例來說,在書籍中,「笑」這個字比「呼吸」更常見。如果機器學習模型是根據書籍語料庫估算笑聲和呼吸的相對頻率,可能會判斷笑聲比呼吸更常見。
詳情請參閱機器學習速成課程中的「公平性:偏見類型」。
兩者的向量表示法
將資料對應至實用特徵的程序。
重新排名
推薦系統的最後階段,在此階段中,系統可能會根據其他 (通常是非機器學習) 演算法,重新評估評分項目。重新排序會評估評分階段產生的項目清單,並採取下列動作:
- 排除使用者已購買的項目。
- 提高較新項目的分數。
詳情請參閱推薦系統課程中的重新排序。
回應
生成式 AI 模型推論的文字、圖片、音訊或影片。換句話說,提示是生成式 AI 模型的輸入內容,而回覆則是輸出內容。
回覆集
檢索增強生成 (RAG)
這項技術可利用模型訓練後檢索到的知識來源建立基準,增進大型語言模型 (LLM) 輸出內容的品質。RAG 可讓經過訓練的 LLM 存取從可信知識庫或文件擷取的資訊,藉此提升 LLM 回覆的準確度。
使用檢索增強生成技術的常見動機包括:
- 提高模型生成回覆的準確度。
- 讓模型存取未經訓練的知識。
- 變更模型使用的知識。
- 讓模型引用來源。
舉例來說,假設化學應用程式使用 PaLM API 生成與使用者查詢相關的摘要。應用程式後端收到查詢時,後端會執行下列操作:
- 搜尋 (「擷取」) 與使用者查詢相關的資料。
- 在使用者查詢中附加 (「擴增」) 相關化學資料。
- 指示 LLM 根據附加資料建立摘要。
回攻
在強化學習中,如果指定政策和狀態,回報值就是代理程式預期在從狀態到集數結尾期間,遵循政策時收到的所有獎勵總和。代理會根據取得獎勵所需的狀態轉換,折算獎勵金額,藉此考量預期獎勵的延遲性質。
因此,如果折扣係數為 \(\gamma\),且 \(r_0, \ldots, r_{N}\)表示集數結束前的獎勵,則回報計算方式如下:
獎勵
在強化學習中,於「狀態」中採取「動作」後獲得的數值結果,由「環境」定義。
嶺迴歸正則化
與 L2 正則化同義。「嶺迴歸正規化」一詞較常出現在純統計學情境中,而「L2 正規化」則較常出現在機器學習情境中。
RNN
循環類神經網路的縮寫。
ROC 曲線
ROC 曲線的形狀代表二元分類模型區分正類和負類的能力。舉例來說,假設二元分類模型完美區分所有負類和正類:
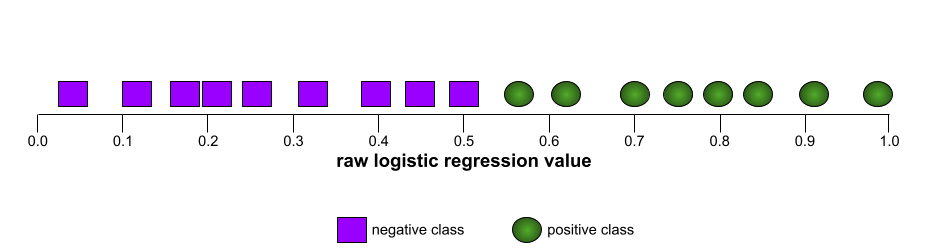
上述模型的 ROC 曲線如下所示:
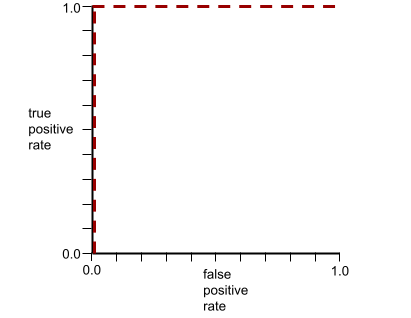
相較之下,下圖繪製出一個糟糕模型的原始邏輯迴歸值,這個模型完全無法區分負面類別和正面類別:
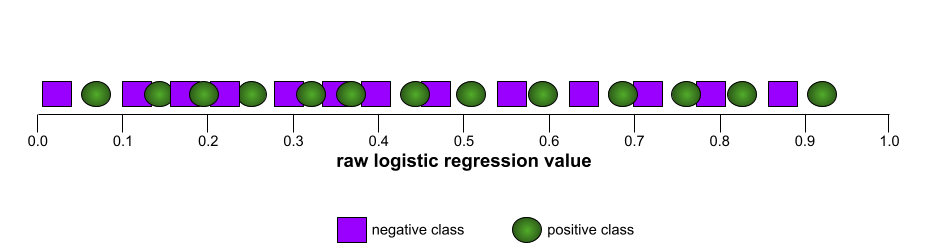
這個模型的 ROC 曲線如下所示:
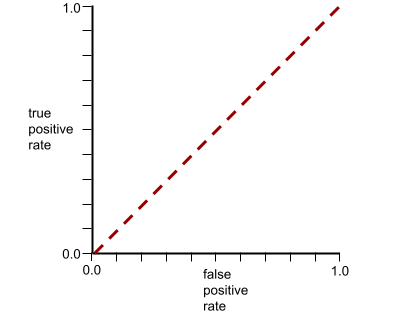
同時,在現實世界中,大多數二元分類模型都會在某種程度上區分正類和負類,但通常不會完美區分。因此,典型的 ROC 曲線會落在兩個極端之間:
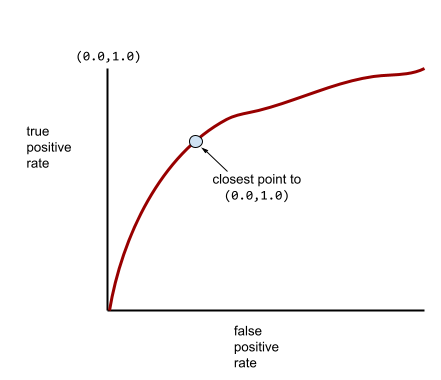
ROC 曲線最接近 (0.0,1.0) 的點,理論上會找出理想的分類門檻。不過,其他幾個現實世界的問題會影響理想分類門檻的選取。舉例來說,偽陰性造成的困擾可能遠大於偽陽性。
AUC 這項數值指標會將 ROC 曲線匯總為單一浮點數值。
角色提示
提示通常以代名詞「你」開頭,會要求生成式 AI 模型在生成回覆時,扮演特定人物或角色。角色提示可協助生成式 AI 模型進入正確的「思維模式」,進而生成更有用的回覆。舉例來說,視您想獲得的回覆類型而定,下列任何角色提示可能都適用:
您擁有電腦科學博士學位。
你是一位軟體工程師,喜歡向程式設計新手耐心說明 Python。
您是動作英雄,具備非常特殊的程式設計技能。 請向我保證您會在 Python 清單中找到特定項目。
根
決策樹中的起始節點 (第一個條件)。按照慣例,圖表會將根節點放在決策樹的頂端。例如:
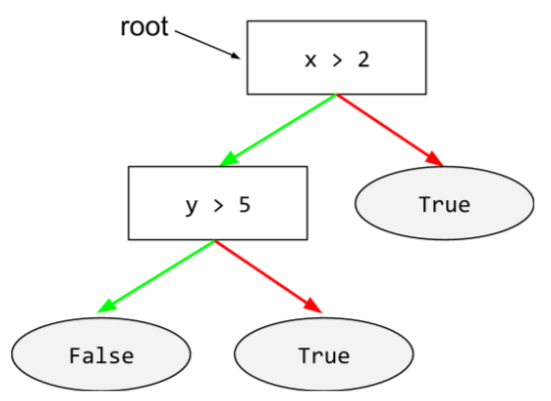
根目錄
您指定的目錄,用於代管多個模型的 TensorFlow 檢查點和事件檔案的子目錄。
均方根誤差 (RMSE)
均方誤差的平方根。
旋轉不變性
在圖片分類問題中,演算法即使在圖片方向改變時,仍能成功分類圖片。舉例來說,演算法仍可辨識網球拍,無論網球拍是朝上、朝側或朝下。請注意,旋轉不變性不一定適用於所有情況;舉例來說,倒過來的 9 不應分類為 9。
ROUGE (Recall-Oriented Understudy for Gisting Evaluation)
這是一系列指標,用於評估自動摘要和機器翻譯模型。ROUGE 指標會判斷參考文字與機器學習模型生成的文字重疊的程度。ROUGE 系列的每個成員都會以不同方式測量重疊程度。ROUGE 分數越高,表示參考文字和生成文字的相似度越高。
每個 ROUGE 系列成員通常會產生下列指標:
- 精確度
- 喚回度
- F1
如需詳細資料和範例,請參閱:
ROUGE-L
ROUGE 系列的指標,著重於參考文字和生成文字中最長共同子序列的長度。下列公式會計算 ROUGE-L 的召回率和精確度:
然後使用 F1,將 ROUGE-L 喚回率和 ROUGE-L 精確度匯總為單一指標:
ROUGE-L 會忽略參考文字和生成文字中的任何換行符,因此最長共同子序列可能會跨越多個句子。如果參考文字和生成的文字包含多個句子,一般來說,ROUGE-Lsum (ROUGE-L 的變體) 是較好的指標。ROUGE-Lsum 會判斷段落中每個句子的最長共同子序列,然後計算這些最長共同子序列的平均值。
ROUGE-N
ROUGE 系列指標集,用於比較參考文字和生成文字中特定大小的共用 N 元語。例如:
- ROUGE-1 會計算參考文字和生成文字中共同的符記數量。
- ROUGE-2 會測量參考文字和生成文字中,共用的二元語法 (2 元語法) 數量。
- ROUGE-3 會測量參考文字和生成文字中,共用三元語法 (3 元語法) 的數量。
您可以使用下列公式,計算 ROUGE-N 系列中任何成員的 ROUGE-N 召回率和 ROUGE-N 精確度:
接著,您可以使用 F1,將 ROUGE-N 喚回率和 ROUGE-N 精確度匯總為單一指標:
ROUGE-S
寬容形式的 ROUGE-N,可啟用 skip-gram 比對。也就是說,ROUGE-N 只會計算完全相符的 N 元語法,但 ROUGE-S 也會計算以一或多個字詞分隔的 N 元語法。舉例來說,您可以嘗試:
計算 ROUGE-N 時,2-gram「White clouds」與「White billowing clouds」不符。不過,在計算 ROUGE-S 時,「White clouds」(白雲)確實與「White billowing clouds」(白色的積雲)相符。
R 平方
迴歸指標,指出標籤的變異程度是由個別特徵或特徵集所造成。R 平方是介於 0 和 1 之間的值,解讀方式如下:
- R 平方值為 0 表示標籤的變異完全與特徵集無關。
- R 平方值為 1 表示標籤的所有變異都是由特徵集所致。
- 介於 0 和 1 之間的 R 平方值,表示可從特定特徵或特徵集預測標籤變異的程度。舉例來說,R 平方值為 0.10 表示標籤的變異數有 10% 是由特徵集造成,R 平方值為 0.20 表示有 20% 是由特徵集造成,依此類推。
日
取樣偏誤
請參閱選擇偏誤。
放回取樣
從一組候選項目中挑選項目,且同一項目可挑選多次。「含替換」一詞表示每次選取後,所選項目會返回候選項目集區。反向方法「無放回抽樣」表示候選項目只能挑選一次。
舉例來說,請考量下列水果組合:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}假設系統隨機挑選 fig 做為第一個項目。
如果使用放回抽樣,系統會從下列集合中挑選第二個項目:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}沒錯,這與先前的設定相同,因此系統可能會再次選取 fig。
如果使用無替代的抽樣方式,一旦選取樣本,就無法再次選取。舉例來說,如果系統隨機選取 fig 做為第一個樣本,就不能再次選取 fig。因此,系統會從下列 (縮減) 集合中挑選第二個樣本:
fruit = {kiwi, apple, pear, cherry, lime, mango}SavedModel
建議用來儲存及復原 TensorFlow 模型的格式。SavedModel 是適用於各語言且可復原的序列化格式,可讓高階系統和工具產生、使用及轉換 TensorFlow 模型。
如需完整詳細資料,請參閱 TensorFlow 程式設計人員指南的「儲存及還原」一節。
平價
負責儲存模型檢查點的 TensorFlow 物件。
純量
單一數字或單一字串,可表示為張量,等級為 0。舉例來說,下列程式碼行會在 TensorFlow 中各建立一個純量:
breed = tf.Variable("poodle", tf.string)
temperature = tf.Variable(27, tf.int16)
precision = tf.Variable(0.982375101275, tf.float64)資源調度
任何數學轉換或技術,可移動標籤、特徵值或兩者的範圍。某些形式的縮放對於正規化等轉換非常有用。
機器學習中常用的縮放形式包括:
- 線性縮放,通常會結合減法和除法,將原始值替換為介於 -1 和 +1 之間,或介於 0 和 1 之間的數字。
- 對數縮放,將原始值替換為對數。
- Z 分數常態化:將原始值替換為浮點值,代表與該特徵平均值的標準差數量。
scikit-learn
熱門的開放原始碼機器學習平台。詳情請參閱 scikit-learn.org。
計分
推薦系統的一部分,可為候選項目產生階段產生的每個項目提供值或排名。
選擇偏誤
由於選取程序會在資料中觀察到的樣本與未觀察到的樣本之間產生系統性差異,因此從樣本資料得出的結論可能會有錯誤。選擇偏誤的形式如下:
- 涵蓋偏誤:資料集中代表的族群與機器學習模型預測的族群不符。
- 取樣偏誤:資料並非從目標群組隨機收集。
- 無回應偏差 (也稱為參與偏差):特定群組的使用者選擇不參與問卷調查的比率,與其他群組的使用者不同。
舉例來說,假設您要建立機器學習模型,預測使用者對電影的喜好程度。如要收集訓練資料,請向電影院前排的所有人發放問卷調查。乍看之下,這似乎是收集資料集的合理方式,但這種資料收集方式可能會導致下列形式的選擇偏差:
- 涵蓋範圍偏差:如果從選擇觀看電影的人口中取樣,模型預測結果可能無法推廣給未對電影表現出同等興趣的使用者。
- 抽樣偏差:您並未從目標母體 (所有電影觀眾) 隨機抽樣,而是只從前排觀眾抽樣。前排觀眾可能比其他排的觀眾更感興趣。
- 無回應偏差:一般而言,與意見溫和的人相比,意見強烈的人往往更常回應選填問卷調查。由於電影問卷調查為選填,因此回應很可能形成雙峰分布,而非常態 (鐘形) 分布。
自注意 (也稱為自注意層)
類神經網路層,可將嵌入序列 (例如 權杖嵌入) 轉換為另一個嵌入序列。輸出序列中的每個嵌入內容,都是透過注意力機制整合輸入序列元素中的資訊所建構而成。
自注意中的「自」是指序列會注意自身,而非其他脈絡。自我注意力是 Transformer 的主要建構區塊之一,並使用字典查詢術語,例如「查詢」、「鍵」和「值」。
自注意力層會從一系列輸入表示法開始,每個字詞各有一個表示法。單字的輸入表示法可以是簡單的嵌入。對於輸入序列中的每個字詞,神經網路會評估該字詞與整個字詞序列中每個元素的相關性。相關性分數會決定字詞的最終表示方式,以及納入其他字詞表示方式的程度。
舉例來說,請看以下句子:
這隻動物太累了,所以沒有過馬路。
下圖 (取自「Transformer: A Novel Neural Network Architecture for Language Understanding」) 顯示代名詞「it」的自注意力層注意力模式,每條線的深淺代表每個字詞對表示法的貢獻程度:
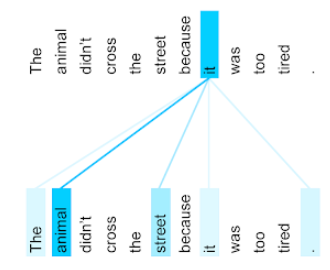
自注意層會醒目顯示與「it」相關的字詞。在本例中,注意力層已學會醒目顯示可能指涉的字詞,並為「動物」指派最高權重。
對於 n 個權杖序列,自我注意力會轉換 n 次嵌入序列,序列中的每個位置各轉換一次。
自我監督式學習
這類技術可將非監督式機器學習問題轉換為監督式機器學習問題,方法是從未標註的範例建立替代標籤。
部分以 Transformer 為基礎的模型 (例如 BERT) 會使用自我監督式學習。
自我監督式訓練是半監督式學習方法。
自修
自我監督式學習的變體,在符合下列所有條件時特別實用:
自我訓練的運作方式是反覆執行下列兩個步驟,直到模型不再進步為止:
- 使用監督式機器學習,根據已加上標籤的範例訓練模型。
- 使用步驟 1 中建立的模型,對未標記的樣本產生預測 (標籤),並將模型判斷結果信心度高的樣本,連同預測標籤移至標記樣本。
請注意,步驟 2 的每次疊代都會為步驟 1 新增更多標示範例,以供訓練。
半監督式學習
根據部分訓練樣本有標籤,但其他樣本沒有標籤的資料訓練模型。半監督式學習的一種技術是推斷未標註範例的標籤,然後根據推斷的標籤進行訓練,建立新模型。如果取得標籤的成本很高,但未標註的範例很多,半監督式學習就很有用。
自我訓練是半監督式學習的一種技術。
敏感屬性
可能因法律、道德、社會或個人因素而受到特別考量的使用者屬性。情緒分析
使用統計或機器學習演算法,判斷群組對服務、產品、機構或主題的整體態度 (正面或負面)。舉例來說,演算法可使用自然語言理解技術,對大學課程的文字意見回饋進行情緒分析,判斷學生普遍喜歡或不喜歡該課程的程度。
詳情請參閱文字分類指南。
序列模型
輸入內容具有序列依附關係的模型。舉例來說,根據先前觀看的影片序列,預測下一個觀看的影片。
序列到序列工作
這項工作會將輸入的符記序列轉換為輸出符記序列。舉例來說,序列對序列的熱門工作有以下兩種:
- 譯者:
- 輸入序列範例:「I love you.」
- 輸出序列範例:「Je t'aime.」
- 回答問題:
- 輸入範例:「我需要開車去紐約市嗎?」
- 輸出內容範例:「否。請將車輛停在家中。」
人份
將訓練好的模型提供給使用者,透過線上推論或離線推論提供預測。
形狀 (張量)
張量每個維度中的元素數量。形狀會以整數清單表示。舉例來說,下列二維張量的形狀為 [3,4]:
[[5, 7, 6, 4], [2, 9, 4, 8], [3, 6, 5, 1]]
TensorFlow 使用以列為主的 (C 樣式) 格式表示維度順序,因此 TensorFlow 中的形狀為 [3,4],而非 [4,3]。換句話說,在二維 TensorFlow 張量中,形狀為 [列數、欄數]。
靜態形狀是指編譯時已知的張量形狀。
動態形狀在編譯時為不明,因此取決於執行階段資料。這個張量可能會以 TensorFlow 中的預留位置維度表示,如 [3, ?] 所示。
shard
訓練集或模型的邏輯劃分。通常,某些程序會將範例或參數分成 (通常) 大小相等的區塊,藉此建立分片。然後將每個分片指派給不同的機器。
模型分片稱為「模型平行處理」;資料分片稱為「資料平行處理」。
縮水
超參數,用於控制梯度提升中的過度擬合。梯度提升的縮減與梯度下降中的學習率類似。縮放比例是介於 0.0 和 1.0 之間的小數值。與較大的縮減值相比,較小的縮減值可更有效地減少過度擬合。
並排比較
比較兩個模型的回覆品質,判斷模型對相同提示的回覆。舉例來說,假設您為兩個不同模型提供下列提示:
製作一隻可愛的狗在玩三顆球的圖像。
在並排評估中,評估人員會選擇「較佳」的圖片 (更準確?更美觀?更可愛?)。
S 函數
這個數學函式會將輸入值「擠壓」到受限範圍內,通常是 0 到 1 或 -1 到 +1。也就是說,您可以將任何數字 (2、100 萬、負 10 億等) 傳遞至 Sigmoid 函數,輸出結果仍會落在受限範圍內。Sigmoid 啟動函式的繪圖如下所示:

Sigmoid 函數在機器學習中有幾種用途,包括:
相似度指標
在分群演算法中,這個指標用於判斷任意兩個樣本的相似程度。
單一程式 / 多個資料 (SPMD)
這項平行處理技術會在不同裝置上,針對不同的輸入資料平行執行相同運算。SPMD 的目標是更快取得結果。這是最常見的平行程式設計風格。
縮放不變性
在圖像分類問題中,演算法即使在圖像大小改變時,仍能成功分類圖像。舉例來說,演算法無論是使用 200 萬像素或 20 萬像素,都能辨識出貓。請注意,即使是最佳的圖像分類演算法,在大小不變性方面仍有實際限制。舉例來說,如果貓咪圖片只佔 20 像素,演算法 (或人) 就不太可能正確分類。
詳情請參閱分群課程。
素描
在非監督式機器學習中,演算法類別會對範例執行初步相似度分析。草圖演算法會使用 位置感應雜湊函式 找出可能相似的點,然後將這些點分組到儲存區。
草圖可減少大型資料集相似度計算所需的運算量。我們不會計算資料集中每對範例的相似度,只會計算每個 bucket 中每對點的相似度。
skip-gram
N 元語法可能會省略 (或「略過」) 原始內容中的字詞,也就是說,N 個字詞原本可能並非相鄰。更精確地說,「k-skip-n-gram」是 n 元語法,最多可略過 k 個字詞。
舉例來說,「the quick brown fox」可能會有以下 2-gram:
- 「the quick」
- 「quick brown」
- 「brown fox」
「1-skip-2-gram」是指兩個字詞之間最多間隔 1 個字詞。因此,「敏捷的棕色狐狸」的 1-skip 2-gram 如下:
- 「the brown」
- 「quick fox」
此外,所有 2-gram 都是 1-skip-2-gram,因為可略過的字詞少於一個。
Skip-gram 有助於進一步瞭解字詞周圍的脈絡。在範例中,「fox」直接與 1-skip-2-gram 集合中的「quick」相關聯,但與 2-gram 集合中的「quick」無關。
Skip-gram 可協助訓練字詞嵌入模型。
softmax
這個函式會判斷多元分類模型中每個可能類別的機率。機率總和必須為 1.0。舉例來說,下表顯示 Softmax 如何分配各種機率:
| 圖片為... | 機率 |
|---|---|
| 狗 | .85 |
| cat | .13 |
| 馬 | .02 |
Softmax 也稱為「完整 softmax」。
與候選人抽樣形成對比。
詳情請參閱機器學習速成課程中的「類神經網路:多類別分類」。
軟提示調整
這項技術可針對特定工作調整大型語言模型,不必進行耗費資源的微調。軟提示調整功能會自動調整提示,達到與重新訓練模型中所有權重相同的目標。
收到文字提示時,軟提示調整通常會將額外的權杖嵌入內容附加至提示,並使用反向傳播來最佳化輸入內容。
「硬」提示包含實際權杖,而非權杖嵌入。
稀疏特徵
值主要為零或空白的特徵。舉例來說,如果特徵包含單一 1 值和一百萬個 0 值,就是稀疏特徵。相反地,密集特徵的值大多不是零或空白。
在機器學習中,有許多特徵都是稀疏特徵。類別特徵通常是稀疏特徵。 舉例來說,森林中可能有 300 種樹木,但單一範例可能只會識別出楓樹。或者,在影片庫中數百萬部可能的影片中,單一範例可能只會識別出「北非諜影」。
在模型中,您通常會使用 one-hot 編碼表示稀疏特徵。如果 one-hot 編碼很大,您可能會在 one-hot 編碼的頂端放置嵌入層,以提高效率。
稀疏表示法
只儲存稀疏特徵中非零元素的位置。
舉例來說,假設名為 species 的類別特徵可識別特定森林中的 36 種樹木。此外,假設每個範例只會識別單一物種。
您可以使用 one-hot 向量表示每個範例中的樹種。獨熱向量會包含單一 1 (代表該範例中的特定樹種) 和 35 個 0 (代表該範例中不存在的 35 個樹種)。因此,maple 的 one-hot 表示法可能如下所示:

或者,稀疏表示法只會識別特定物種的位置。如果 maple 位於位置 24,則 maple 的稀疏表示法會是:
24
請注意,稀疏表示法比 one-hot 表示法精簡許多。
詳情請參閱機器學習速成課程中的「使用類別型資料」。
稀疏向量
稀疏度
向量或矩陣中設為零 (或空值) 的元素數量,除以該向量或矩陣中的項目總數。舉例來說,假設有一個 100 個元素的矩陣,其中 98 個儲存格包含零。稀疏度的計算方式如下:
特徵稀疏性是指特徵向量的稀疏性;模型稀疏性是指模型權重的稀疏性。
空間彙整
請參閱集區。
specificational coding
以人類語言 (例如英文) 編寫及維護檔案,說明軟體。然後,您可以請生成式 AI 模型或其他軟體工程師,根據該說明建立軟體。
自動生成的程式碼通常需要經過疊代。在規格編碼中,您會疊代說明檔。相較之下,在對話式程式碼編寫中,您會在提示方塊中疊代。在實務上,自動生成程式碼有時會結合規格化編碼和對話式編碼。
分割
分割器
訓練決策樹時,負責在每個節點尋找最佳條件的常式 (和演算法)。
SPMD
單一程式 / 多個資料的縮寫。
SQuAD
史丹佛問答資料集的縮寫,在論文《SQuAD:100,000+ Questions for Machine Comprehension of Text》中介紹。這個資料集中的問題來自使用者對維基百科文章提出的問題。SQuAD 中的部分問題有答案,但其他問題刻意沒有答案。因此,您可以使用 SQuAD 評估 LLM 的能力,判斷模型是否能:
- 回答可以回答的問題。
- 找出無法回答的問題。
完全比對搭配 F1 是評估 LLM 相對 SQuAD 的最常見指標。
平方轉折損失
轉折損失的平方。平方轉折損失對離群值的懲罰比一般轉折損失更嚴厲。
平方損失
L2 損失 的同義詞。
階段式訓練
這項策略會分階段訓練模型。目標可以是加快訓練程序,或是提升模型品質。
以下是漸進式堆疊方法的說明圖:
- 第 1 階段包含 3 個隱藏層,第 2 階段包含 6 個隱藏層,第 3 階段則包含 12 個隱藏層。
- 第 2 階段會使用第 1 階段 3 個隱藏層中學到的權重開始訓練。第 3 階段會使用第 2 階段 6 個隱藏層中學到的權重,開始訓練。
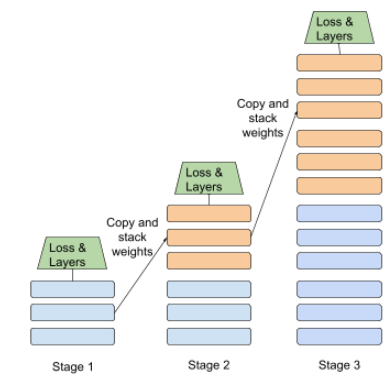
另請參閱「管道化」。
州
在強化學習中,參數值會說明環境的目前設定,代理程式會使用這些參數值選擇動作。
狀態動作價值函式
Q 函式的同義詞。
靜態
一次性作業,而非持續進行的作業。 「靜態」和「離線」是同義詞。 以下是機器學習中 static 和 offline 的常見用途:
- 靜態模型 (或離線模型) 是指訓練一次後,可使用一段時間的模型。
- 靜態訓練 (或離線訓練) 是指訓練靜態模型的過程。
- 靜態推論 (或離線推論) 是指模型一次生成一批預測結果的程序。
與動態對比。
靜態推論
離線推論的同義詞。
平穩性
值在一或多個維度 (通常是時間) 中不會變更的特徵。舉例來說,如果特徵在 2021 年和 2023 年的值大致相同,就表示該特徵具有平穩性。
在現實世界中,很少有特徵呈現平穩性。即使是與穩定性同義的特徵 (例如海平面),也會隨時間變化。
與非平穩性形成對比。
點選 [下一步]
一個批次的前向傳遞和後向傳遞。
如要進一步瞭解正向傳遞和反向傳遞,請參閱反向傳播。
步距
學習率的同義詞。
隨機梯度下降 (SGD)
梯度下降演算法,其中批次大小為 1。換句話說,SGD 會從訓練集中隨機選擇一個範例進行訓練。
詳情請參閱機器學習速成課程中的「線性迴歸:超參數」。
步幅
在卷積運算或集區化中,下一系列輸入切片的每個維度都會有差異。舉例來說,下列動畫展示了卷積運算期間的 (1,1) 步幅。因此,下一個輸入片段會從前一個輸入片段右側的一個位置開始。當作業到達右側邊緣時,下一個切片會向左移動,但會向下一個位置移動。
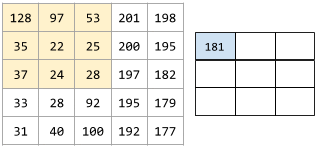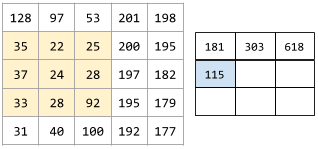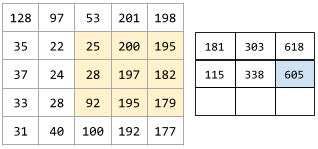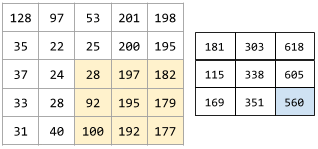
上例示範的是二維步幅。如果輸入矩陣是三維,步幅也會是三維。
結構風險最小化 (SRM)
這項演算法會兼顧兩大目標:
- 需要建構預測能力最強的模型 (例如損失最低)。
- 需要盡可能簡化模型 (例如強正規化)。
舉例來說,在訓練集上將損失 + 正規化降到最低的函式,就是結構風險最小化演算法。
與經驗風險最小化形成對比。
向下取樣
請參閱集區。
子字詞權杖
舉例來說,「itemize」一字可能會拆解為「item」(字根) 和「ize」(字尾),每個部分都以自己的符記表示。將不常見的字詞拆成這些片段 (稱為子字詞),可讓語言模型處理字詞中較常見的組成部分,例如前置字元和後置字元。
反之,「going」等常見字詞可能不會拆開,而是以單一符記表示。
摘要
在 TensorFlow 中,於特定步驟計算出的值或一組值,通常用於在訓練期間追蹤模型指標。
監督式機器學習
從特徵和對應的標籤訓練模型。監督式機器學習類似於學習某個主題,方法是研究一組問題及其對應的答案。掌握問題與答案之間的對應關係後,學生就能回答同一主題的新問題 (從未見過的問題)。
與非監督式機器學習比較。
詳情請參閱「機器學習簡介」課程的「監督式學習」。
合成特徵
特徵並未出現在輸入特徵中,但由一或多個輸入特徵組合而成。建立合成特徵的方法包括:
- 分組:將連續特徵分組到範圍值區。
- 建立特徵交集。
- 將一個特徵值乘以 (或除以) 其他特徵值或本身。舉例來說,如果
a和b是輸入特徵,則下列為合成特徵的範例:- ab
- a2
- 將超越函數套用至特徵值。舉例來說,如果
c是輸入特徵,則下列為合成特徵的範例:- sin(c)
- ln(c)
T
T5
這是 Google AI 在 2020 年推出的轉移學習 模型,可將文字轉換為文字。 T5 是以 Transformer 架構為基礎的編碼器-解碼器模型,並使用極為龐大的資料集進行訓練。這類模型擅長處理各種自然語言處理工作,例如生成文字、翻譯語言,以及以對話方式回答問題。
T5 的名稱來自「Text-to-Text Transfer Transformer」中的五個字母 T。
T5X
開放原始碼的機器學習架構,專為建構及訓練大規模自然語言處理 (NLP) 模型而設計。T5 是在 T5X 程式碼集上實作 (以 JAX 和 Flax 為基礎)。
表格型 Q-learning
在強化學習中,實作 Q-learning 時,會使用表格儲存每個狀態和動作組合的 Q 函式。
目標
label 的同義詞。
目標聯播網
在深度 Q 學習中,類神經網路是主要類神經網路的穩定近似值,而主要類神經網路會實作 Q 函式或政策。接著,您可以使用目標網路預測的 Q 值訓練主要網路。因此,您可以避免主要網路根據自身預測的 Q 值進行訓練時,發生回饋迴路。避免這類意見回饋可提高訓練穩定性。
任務
可使用機器學習技術解決的問題,例如:
溫度
超參數,可控制模型輸出內容的隨機程度。溫度越高,輸出內容的隨機性就越高;溫度越低,輸出內容的隨機性就越低。
選擇最佳溫度取決於特定應用程式和/或字串值。
時序資料
在不同時間點記錄的資料。舉例來說,一年中每天記錄的冬季外套銷售量就是時間資料。
Tensor
TensorFlow 程式中的主要資料結構。張量是 N 維 (N 可能非常大) 資料結構,最常見的是純量、向量或矩陣。Tensor 的元素可以保存整數、浮點數或字串值。
TensorBoard
這個資訊主頁會顯示執行一或多個 TensorFlow 程式期間儲存的摘要。
TensorFlow
大規模分散式機器學習平台。這個詞彙也指 TensorFlow 堆疊中的基本 API 層,支援資料流圖的一般運算。
雖然 TensorFlow 主要用於機器學習,但您也可以將 TensorFlow 用於非機器學習工作,這類工作需要使用資料流圖形進行數值運算。
TensorFlow Playground
這項程式會以視覺化方式呈現不同的超參數如何影響模型 (主要是神經網路) 訓練。前往 http://playground.tensorflow.org ,試用 TensorFlow Playground。
TensorFlow Serving
用於在實際工作環境中部署訓練好的模型。
Tensor Processing Unit (TPU)
特殊應用積體電路 (ASIC),可提升機器學習工作負載的效能。這些 ASIC 會以多個 TPU 晶片的形式部署在 TPU 裝置上。
張量的秩
請參閱「秩 (張量)」。
張量形狀
Tensor在各個維度中包含的元素數量。舉例來說,[5, 10] 張量在一個維度中的形狀為 5,在另一個維度中則為 10。
張量大小
Tensor所含的純量總數。舉例來說,[5, 10] 張量的大小為 50。
TensorStore
這個程式庫可有效率地讀取及寫入大型多維陣列。
終止條件
在強化學習中,決定集數何時結束的條件,例如代理程式達到特定狀態或超過狀態轉換的門檻次數。舉例來說,在井字遊戲中,當玩家標記三個連續空格,或所有空格都標記完畢時,一集就會結束。
test
測試損失
代表模型對測試集的損失的指標。建構模型時,您通常會盡量減少測試損失。這是因為相較於低訓練損失或低驗證損失,低測試損失是更強大的品質信號。
如果測試損失與訓練損失或驗證損失之間存在巨大差距,有時表示您需要提高正規化率。
測試集
傳統上,資料集中的範例會分成下列三個不同的子集:
資料集中的每個範例都只能屬於上述其中一個子集。舉例來說,單一範例不應同時屬於訓練集和測試集。
訓練集和驗證集都與模型訓練密切相關。 由於測試集只與訓練間接相關,因此測試損失是比訓練損失或驗證損失更優質且偏差較少的指標。
詳情請參閱機器學習速成課程中的「資料集:分割原始資料集」。
文字範圍
與文字字串特定子區段相關聯的陣列索引範圍。
舉例來說,Python 字串 s="Be good now" 中的字詞 good 佔用從 3 到 6 的文字範圍。
tf.Example
標準通訊協定緩衝區,用於說明機器學習模型訓練或推論的輸入資料。
tf.keras
整合至 TensorFlow 的 Keras 實作項目。
門檻 (適用於決策樹)
在軸對齊條件中,特徵要比較的值。舉例來說,在下列條件中,75 是門檻值:
grade >= 75
詳情請參閱決策樹林課程中的「Exact splitter for binary classification with numerical features」。
時間序列分析
機器學習和統計學的子領域,用於分析時間序列資料。許多類型的機器學習問題都需要時間序列分析,包括分類、分群、預測和異常偵測。舉例來說,您可以根據歷來銷售資料,使用時間序列分析按月預測冬季大衣的未來銷售量。
timestep
循環類神經網路中的一個「未捲動」儲存格。舉例來說,下圖顯示三個時間步 (標示為 t-1、t 和 t+1 下標):

token
在語言模型中,模型訓練和預測所用的最小單位。權杖通常是下列其中一種:
- 一個字,例如「狗喜歡貓」這個詞組包含三個字詞符記:「狗」、「喜歡」和「貓」。
- 一個字元,例如「bike fish」這個詞組包含九個字元權杖。(請注意,空白字元也算做一個符記)。
- 子字詞:單一字詞可以是單一符記或多個符記。子字詞由字根、前置字串或後置字串組成。舉例來說,如果語言模型使用子字做為權杖,可能會將「dogs」一字視為兩個權杖 (字根「dog」和複數後綴「s」)。同一個語言模型可能會將單字「taller」視為兩個子字 (字根「tall」和字尾「er」)。
在語言模型以外的網域中,權杖可以代表其他種類的原子單元。舉例來說,在電腦視覺中,權杖可能是圖片的子集。
詳情請參閱機器學習速成課程中的大型語言模型。
tokenizer
這類系統或演算法會將一連串的輸入資料轉換為符記。
大多數現代基礎模型都是多模態,多模態系統的權杖化工具必須將每種輸入類型轉換為適當格式。舉例來說,如果輸入資料包含文字和圖像,權杖化工具可能會將輸入文字轉換為子字,並將輸入圖片轉換為小塊。然後,權杖化工具必須將所有權杖轉換為單一統一的嵌入空間,模型才能「瞭解」多模態輸入串流。
前 k 項準確率
在生成清單的前 k 個位置中,「目標標籤」出現的百分比。清單可以是個人化建議,也可以是依 softmax 排序的項目清單。
Top-k 準確率也稱為「k 準確率」。
塔
深層類神經網路的元件,本身也是深層類神經網路。在某些情況下,每個塔式結構都會從獨立的資料來源讀取資料,且這些塔式結構會保持獨立,直到輸出內容在最終層級中合併為止。在其他情況下 (例如在編碼器和解碼器塔中,有許多 Transformer),塔之間會彼此交叉連接。
毒性
內容是否具有辱罵、威脅或令人反感的程度。許多機器學習模型都能辨識及評估毒性。這類模型大多會根據多項參數 (例如濫用和威脅性語言的程度) 判斷是否含有有害內容。
TPU
TPU 晶片
可程式化的線性代數加速器,搭載晶片內高頻寬記憶體,專為機器學習工作負載最佳化。TPU 裝置上部署了多個 TPU 晶片。
TPU 裝置
印刷電路板 (PCB),內含多個 TPU 晶片、高頻寬網路介面和系統冷卻硬體。
TPU 節點
Google Cloud 上的 TPU 資源,具有特定 TPU 類型。TPU 節點會從對等互連虛擬私有雲網路連線至虛擬私有雲網路。TPU 節點是 Cloud TPU API 中定義的資源。
TPU Pod
Google 資料中心內的TPU 裝置特定配置。TPU Pod 中的所有裝置都會透過專用高速網路互相連線。TPU Pod 是特定 TPU 版本可用的最大TPU 裝置配置。
TPU 資源
您在 Google Cloud 上建立、管理或使用的 TPU 實體。舉例來說,TPU 節點和 TPU 類型都是 TPU 資源。
TPU 配量
TPU 配量是 TPU Pod 中 TPU 裝置的一小部分。TPU 配量中的所有裝置都會透過專用高速網路互相連線。
TPU 類型
一或多個 TPU 裝置的設定,具有特定 TPU 硬體版本。在 Google Cloud 上建立 TPU 節點時,您會選取 TPU 類型。舉例來說,v2-8 TPU 類型是具有 8 個核心的單一 TPU v2 裝置。v3-2048 TPU 類型有 256 部聯網 TPU v3 裝置,總共有 2048 個核心。TPU 類型是Cloud TPU API 中定義的資源。
TPU 工作站
在主機上執行的程序,可在 TPU 裝置上執行機器學習程式。
訓練
決定構成模型的理想參數 (權重和偏差) 的過程。在訓練期間,系統會讀取範例,並逐步調整參數。訓練會使用每個範例,次數從幾次到數十億次不等。
詳情請參閱「機器學習簡介」課程的「監督式學習」。
訓練損失
代表模型在特定訓練疊代期間的損失指標。舉例來說,假設損失函式為平均平方誤差。舉例來說,第 10 次疊代的訓練損失 (均方誤差) 為 2.2,第 100 次疊代的訓練損失為 1.9。
損失曲線會繪製訓練損失與疊代次數的關係圖。損失曲線可提供下列訓練提示:
- 如果斜率向下,表示模型正在進步。
- 向上傾斜表示模型品質變差。
- 平緩的斜率表示模型已達到收斂。
舉例來說,以下經過某種程度理想化的損失曲線顯示:
- 在初始反覆執行階段,斜率大幅下降,表示模型快速改善。
- 斜率逐漸趨緩 (但仍向下),直到訓練接近尾聲為止,這表示模型持續進步,但速度比初期反覆執行階段稍慢。
- 訓練結束時斜率趨緩,表示模型已收斂。
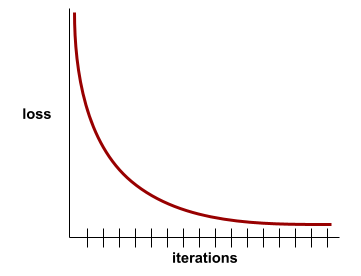
雖然訓練損失很重要,但請參閱一般化。
訓練/應用偏差
訓練集
傳統上,資料集中的樣本會分成下列三個不同的子集:
理想情況下,資料集中的每個樣本都應只屬於上述其中一個子集。舉例來說,單一範例不應同時屬於訓練集和驗證集。
詳情請參閱機器學習速成課程中的「資料集:分割原始資料集」。
軌跡
在強化學習中,一連串的元組代表代理程式的一連串狀態轉換,其中每個元組都對應至特定狀態轉換的狀態、動作、獎勵和下一個狀態。
遷移學習
將資訊從一個機器學習工作轉移至另一個工作。舉例來說,在多工學習中,單一模型會解決多項工作,例如深層模型,這類模型會為不同工作提供不同的輸出節點。遷移學習可能涉及將較簡單工作的解決方案知識轉移至較複雜的工作,或將資料較多的工作知識轉移至資料較少的工作。
大多數機器學習系統都只解決單一工作。遷移學習是人工智慧的一小步,單一程式可以解決多項工作。
Transformer
Google 開發的神經網路架構,採用自我注意力機制,將輸入嵌入序列轉換為輸出嵌入序列,而不依賴捲積或遞迴神經網路。Transformer 可視為一疊自注意層。
轉換器可包含下列任一項目:
編碼器會將嵌入序列轉換為長度相同的新序列。編碼器包含 N 個相同層,每個層都包含兩個子層。這兩個子層會套用至輸入嵌入序列的每個位置,將序列的每個元素轉換為新的嵌入。第一個編碼器子層會匯總輸入序列中的資訊。第二個編碼器子層會將匯總資訊轉換為輸出嵌入。
解碼器會將輸入嵌入序列轉換為輸出嵌入序列,長度可能不同。解碼器也包含 N 個相同層,其中有三個子層,兩個子層與編碼器子層類似。第三個解碼器子層會接收編碼器的輸出內容,並套用自注意機制,從中收集資訊。
網誌文章「Transformer:語言理解的全新類神經網路架構」對 Transformer 做了很好的介紹。
詳情請參閱機器學習速成課程中的「大型語言模型:什麼是大型語言模型?」。
平移不變性
在圖像分類問題中,演算法即使在圖像中物體的位置改變時,仍能成功分類圖像的能力。舉例來說,無論狗位於影格中央或左端,演算法都能辨識。
trigram
三元語法,其中 N=3。
真陰性 (TN)
舉例來說,模型正確預測負類。舉例來說,模型推斷某封電子郵件不是垃圾郵件,而該電子郵件確實不是垃圾郵件。
真陽性 (TP)
舉例來說,模型正確預測正類。舉例來說,模型推斷特定電子郵件是垃圾郵件,而該電子郵件確實是垃圾郵件。
真陽率 (TPR)
與「召回」語法相同。也就是:
真陽率是 ROC 曲線的 y 軸。
存留時間
存留時間的縮寫。
U
Ultra
參數最多的 Gemini 模型。詳情請參閱「Gemini Ultra」。
未察覺 (敏感屬性)
存在敏感屬性,但未納入訓練資料。由於敏感屬性通常與資料的其他屬性相關聯,因此即使模型訓練時未考量敏感屬性,仍可能對該屬性造成差異影響,或違反其他公平性限制。
欠擬合
模型未能充分掌握訓練資料的複雜度,導致模型的預測能力不佳。許多問題都可能導致欠擬合,包括:
詳情請參閱機器學習速成課程中的「過度擬合」。
欠採樣
從類別不平衡的資料集中移除多數類別的範例,建立更平衡的訓練集。
舉例來說,假設資料集中多數類別與少數類別的比例為 20:1。為解決這個類別不平衡的問題,您可以建立訓練集,其中包含所有少數類別的樣本,但只包含十分之一的多數類別樣本,這樣訓練集的類別比例就會是 2:1。由於採用欠採樣,這個更平衡的訓練集可能會產生更優質的模型。或者,這個更均衡的訓練集可能包含的範例不足,無法訓練出有效的模型。
與過度取樣形成對比。
單向
這個系統只會評估目標文字區段之前的文字。相較之下,雙向系統會評估目標文字區段「之前」和「之後」的文字。詳情請參閱雙向。
單向語言模型
語言模型:這類模型只會根據目標權杖之前出現的權杖計算機率,不會根據目標權杖之後出現的權杖計算機率。與雙向語言模型形成對比。
無標籤樣本
包含特徵,但不含標籤的範例。 舉例來說,下表顯示房屋估價模型中的三個未標記範例,每個範例都有三項特徵,但沒有房屋價值:
| 臥室數量 | 浴室數量 | 房屋屋齡 |
|---|---|---|
| 3 | 2 | 15 |
| 2 | 1 | 72 |
| 4 | 2 | 34 |
在監督式機器學習中,模型會根據加上標籤的範例進行訓練,並對未加上標籤的範例做出預測。
請比較有標籤樣本和無標籤樣本。
非監督式機器學習
訓練模型,找出資料集中的模式,通常是未標記的資料集。
非監督式機器學習最常見的用途是將資料分群,分成類似範例的群組。舉例來說,非監督式機器學習演算法可以根據音樂的各種屬性,將歌曲分群。產生的叢集可做為其他機器學習演算法的輸入內容 (例如音樂推薦服務)。如果沒有或很少有實用標籤,分群功能就很有幫助。 舉例來說,在反濫用和詐欺等領域,叢集可協助使用者進一步瞭解資料。
與監督式機器學習形成對比。
詳情請參閱「機器學習簡介」課程中的「什麼是機器學習?」。
升幅模型
這項模型技術常用於行銷領域,可模擬「處理」對「個人」的「因果效應」(也稱為「增量影響」)。我們來看看下面兩個範例:
- 醫生可能會使用提升模型,根據病患 (個人) 的年齡和病史,預測醫療程序 (治療) 的死亡率降幅 (因果效應)。
- 行銷人可能會使用升幅模型,預測廣告 (處理) 對個人造成的購買機率增加 (因果效應)。
升幅模型與分類或迴歸不同,因為升幅模型一律會缺少部分標籤 (例如二元處理中的一半標籤)。舉例來說,病患可能接受治療,也可能不接受治療;因此,我們只能觀察病患在其中一種情況下是否會痊癒 (但絕不會同時觀察兩種情況)。升幅模型的主要優點是可針對未觀察到的情況 (反事實) 產生預測,並用於計算因果效應。
加權
將權重套用至 下採樣類別,權重值等於下採樣的因數。
使用者矩陣
在推薦系統中,矩陣分解會產生嵌入向量,其中包含使用者偏好的潛在信號。使用者矩陣的每一列都包含單一使用者各種潛在信號的相對強度資訊。舉例來說,假設有電影推薦系統。在這個系統中,使用者矩陣中的潛在信號可能代表每位使用者對特定類型的興趣,也可能是不易解讀的信號,涉及多個因素的複雜互動。
使用者矩陣的每一欄代表一個潛在特徵,每一列代表一位使用者。 也就是說,使用者矩陣的資料列數量與要進行因數分解的目標矩陣相同。舉例來說,如果電影推薦系統有 1,000,000 位使用者,使用者矩陣就會有 1,000,000 列。
V
驗證
模型的初步品質評估結果。 驗證會根據驗證集檢查模型預測的品質。
您可以將針對驗證集評估模型視為第一輪測試,而針對測試集評估模型則視為第二輪測試。
驗證損失
另請參閱一般化曲線。
驗證集
資料集的子集,用於對訓練完成的模型進行初步評估。通常您會先針對驗證集多次評估訓練好的模型,再針對測試集評估模型。
傳統上,您會將資料集中的範例分成下列三個不同的子集:
理想情況下,資料集中的每個樣本都應只屬於上述其中一個子集。舉例來說,單一範例不應同時屬於訓練集和驗證集。
詳情請參閱機器學習速成課程中的「資料集:分割原始資料集」。
價值插補
以可接受的替代值取代遺漏值的程序。如果缺少值,您可以捨棄整個範例,也可以使用值插補來挽救範例。
舉例來說,假設資料集包含 temperature 特徵,且應每小時記錄一次。不過,系統無法提供特定時段的溫度讀數。以下是資料集的一部分:
| 時間戳記 | 溫度 |
|---|---|
| 1680561000 | 10 |
| 1680564600 | 12 |
| 1680568200 | 遺漏 |
| 1680571800 | 20 |
| 1680575400 | 21 |
| 1680579000 | 21 |
系統可能會刪除缺少的範例,或根據插補演算法,將缺少的溫度插補為 12、16、18 或 20。
梯度消失問題
某些深層類神經網路的早期隱藏層梯度會變得異常平緩 (低)。梯度越小,深層類神經網路中節點的權重變化就越小,導致學習效果不佳或沒有學習效果。如果模型出現梯度消失問題,訓練就會變得困難或無法進行。長期短期記憶單元可解決這個問題。
請與梯度爆炸問題比較。
變數重要性
一組分數,代表各特徵對模型的重要性。
舉例來說,假設您要使用決策樹估算房價。假設這個決策樹使用三項特徵:尺寸、年齡和風格。如果計算出三個特徵的變數重要性為 {size=5.8, age=2.5, style=4.7},則對決策樹而言,尺寸比年齡或風格更重要。
變數重要性指標有很多種,可讓 ML 專家瞭解模型的不同層面。
變分自動編碼器 (VAE)
一種自動編碼器,可利用輸入和輸出之間的差異,產生輸入內容的修改版本。變分自動編碼器適用於生成式 AI。
VAE 是以變分推論為基礎,這項技術可用於估算機率模型的參數。
向量
這個詞彙的意義非常廣泛,在不同數學和科學領域中各有不同。在機器學習中,向量有兩項屬性:
- 資料型別:機器學習中的向量通常會保留浮點數。
- 元素數量:這是向量的長度或維度。
舉例來說,假設特徵向量包含八個浮點數。這個特徵向量的長度或維度為八。 請注意,機器學習向量通常有大量維度。
您可以將許多不同種類的資訊表示為向量。例如:
- 地球表面的任何位置都可以表示為 2 維向量,其中一個維度是緯度,另一個是經度。
- 500 檔股票的目前價格可以表示為 500 維向量。
- 有限數量的類別機率分布可以向量表示。舉例來說,如果多元分類系統會預測三種輸出顏色 (紅色、綠色或黃色) 的其中一種,則可輸出向量
(0.3, 0.2, 0.5),表示P[red]=0.3, P[green]=0.2, P[yellow]=0.5。
向量可以串連,因此各種不同的媒體都能以單一向量表示。部分模型會直接對許多one-hot 編碼的串連進行運算。
TPU 等專用處理器經過最佳化,可對向量執行數學運算。
Vertex
Google Cloud 的 AI 和機器學習平台。Vertex 提供多種工具和基礎架構,可建構、部署及管理 AI 應用程式,包括存取 Gemini 模型。直覺式程式開發
提示生成式 AI 模型建立軟體。也就是說,提示會說明軟體的用途和功能,生成式 AI 模型則會將提示轉換為原始碼。產生的程式碼不一定符合您的意圖,因此通常需要疊代。
Andrej Karpathy 在這則 X 貼文中提出「氛圍編碼」一詞。 在 X 貼文中,Karpathy 將其描述為「一種新的程式碼編寫方式...完全投入氛圍...」因此,這個詞彙原本是指有意寬鬆的軟體建立方法,您甚至可能不會檢查產生的程式碼。不過,這個詞彙在許多領域迅速演變,現在是指任何形式的 AI 生成程式碼。
如要進一步瞭解氛圍編碼,請參閱 什麼是直覺式程式開發?
此外,請比較直覺式程式開發與下列項目的異同:
W
Wasserstein 損失
這是生成對抗網路中常用的損失函式之一,以生成資料和真實資料分布之間的地球移動距離為依據。
重量
模型要與另一個值相乘的值。 訓練是決定模型理想權重的程序;推論則是使用這些學到的權重進行預測的程序。
詳情請參閱機器學習速成課程中的線性迴歸。
加權交替最小平方 (WALS)
在矩陣因式分解期間,用於盡量減少推薦系統中目標函式的演算法,可降低遺漏範例的權重。WALS 會交替修正列因數分解和欄因數分解,盡量減少原始矩陣與重構矩陣之間的加權平方誤差。這些最佳化問題都可以透過最小平方法凸面最佳化解決。詳情請參閱推薦系統課程。
加權總和
所有相關輸入值乘以對應權重的總和。舉例來說,假設相關輸入內容如下:
| 輸入值 | 輸入權重 |
| 2 | -1.3 |
| -1 | 0.6 |
| 3 | 0.4 |
因此加權總和為:
weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0
加權總和是啟動函式的輸入引數。
寬模型
線性模型,通常具有許多稀疏輸入特徵。我們稱之為「廣泛」,因為這類模型是類神經網路的特殊類型,具有大量直接連線至輸出節點的輸入。與深層模型相比,寬鬆模型通常更容易偵錯和檢查。 雖然寬模型無法透過隱藏層表示非線性,但寬模型可以使用特徵交叉和分組等轉換,以不同方式模擬非線性。
與深層模型形成對比。
寬度
群眾智慧
這個概念是指,平均大量人群 (「群眾」) 的意見或估計值,通常會產生出乎意料的好結果。舉例來說,假設有一款遊戲是讓玩家猜測大罐子裡裝了多少顆軟糖。雖然大多數人的猜測都不準確,但實證結果顯示,所有猜測的平均值與罐子裡實際的糖豆數量非常接近。
集合是群眾智慧的軟體類比。 即使個別模型做出極度不準確的預測,平均多個模型的預測結果通常會產生出乎意料的良好預測。舉例來說,雖然個別決策樹可能做出不佳的預測,但決策樹林通常會做出非常準確的預測。
字詞嵌入
以嵌入向量表示字集中的每個字詞,也就是將每個字詞表示為介於 0.0 和 1.0 之間的浮點值向量。與不同意義的字詞相比,意義相似的字詞會有更相似的表示方式。舉例來說,紅蘿蔔、芹菜和小黃瓜的表示方式會相對類似,但與飛機、太陽眼鏡和牙膏的表示方式則大相逕庭。
X
XLA (加速線性代數)
開放原始碼機器學習編譯器,適用於 GPU、CPU 和機器學習加速器。
XLA 編譯器會採用熱門機器學習架構 (例如 PyTorch、TensorFlow 和 JAX) 的模型,並針對 GPU、CPU 和機器學習加速器等各種硬體平台進行最佳化,以高效執行。
Z
零樣本學習
這是一種機器學習訓練,模型會針對未接受過特定訓練的工作推斷預測結果。換句話說,模型會收到零個特定任務的訓練範例,但需要對該任務進行推論。
零樣本提示
| 提示的組成部分 | 附註 |
|---|---|
| 指定國家/地區的官方貨幣為何? | 您希望 LLM 回答的問題。 |
| 印度: | 實際查詢。 |
大型語言模型可能會回覆下列任一內容:
- 盧比符號
- 印度盧比
- ₹
- 印度盧比
- 盧比
- 印度盧比
所有答案都正確,但您可能會偏好特定格式。
比較並對照零樣本提示與下列術語:
標準分數正規化
縮放技術,可將原始特徵值替換為浮點值,代表該特徵與平均值的標準差數。舉例來說,假設某項特徵的平均值為 800,標準差為 100。下表顯示 Z 分數常態化如何將原始值對應至 Z 分數:
| 原始值 | Z 分數 |
|---|---|
| 800 | 0 |
| 950 | +1.5 |
| 575 | -2.25 |
接著,機器學習模型會根據該特徵的 Z 分數而非原始值進行訓練。
詳情請參閱機器學習速成課程中的「數值資料:正規化」。
本詞彙表定義了機器學習用語。