На этой странице представлены термины глоссария метрик. Для просмотра всех терминов глоссария нажмите здесь .
А
точность
Количество правильных классификационных прогнозов, деленное на общее количество прогнозов. То есть:
Например, модель, сделавшая 40 правильных и 10 неправильных прогнозов, будет иметь точность:
Бинарная классификация предоставляет конкретные названия для различных категорий правильных и неправильных прогнозов . Таким образом, формула точности для бинарной классификации выглядит следующим образом:
где:
- TP — это количество истинно положительных результатов (правильных прогнозов).
- TN — это количество истинно отрицательных результатов (правильных предсказаний).
- FP — это количество ложноположительных результатов (неверных прогнозов).
- FN — это количество ложноотрицательных результатов (неверных прогнозов).
Сравните и сопоставьте точность с прецизией и полнотой .
Дополнительную информацию см. в разделе «Классификация: точность, полнота, прецизионность и связанные с ними показатели» в кратком курсе по машинному обучению.
площадь под кривой PR
См. PR AUC (площадь под кривой PR) .
площадь под кривой ROC
См. AUC (площадь под ROC-кривой) .
AUC (Площадь под ROC-кривой)
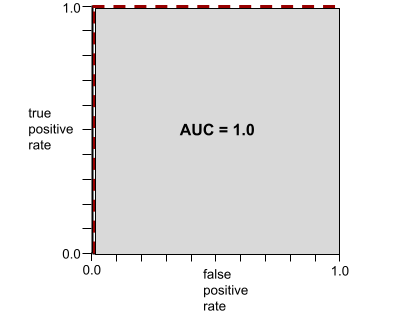
Число от 0,0 до 1,0, представляющее способность модели бинарной классификации разделять положительные и отрицательные классы . Чем ближе AUC к 1,0, тем лучше модель способна разделять классы.
Например, на следующем рисунке показана модель классификации , которая идеально разделяет положительные классы (зеленые овалы) от отрицательных классов (фиолетовые прямоугольники). Эта нереалистично идеальная модель имеет показатель AUC, равный 1,0:

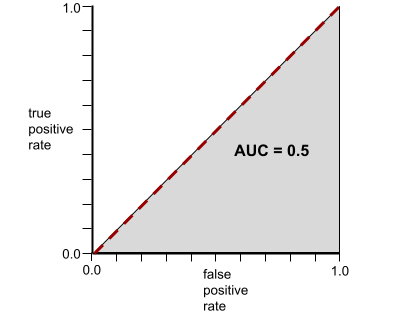
Напротив, на следующем рисунке показаны результаты для модели классификации , которая генерировала случайные результаты. Для этой модели показатель AUC равен 0,5:

Да, у предыдущей модели показатель AUC равен 0,5, а не 0,0.
Большинство моделей находятся где-то между этими двумя крайностями. Например, следующая модель несколько разделяет положительные и отрицательные значения, и поэтому имеет AUC где-то между 0,5 и 1,0:

AUC игнорирует любые значения, которые вы задаете для порога классификации . Вместо этого AUC учитывает все возможные пороги классификации.
Дополнительную информацию см. в разделе «Классификация: ROC и AUC в экспресс-курсе по машинному обучению».
средняя точность при k
Метрика, суммирующая производительность модели при обработке одного запроса, генерирующего ранжированные результаты, например, нумерованный список рекомендаций книг. Средняя точность в точке k — это, собственно, среднее значение точности в точке k для каждого релевантного результата. Формула для расчета средней точности в точке k выглядит следующим образом:
\[{\text{average precision at k}} = \frac{1}{n} \sum_{i=1}^n {\text{precision at k for each relevant item} } \]
где:
- \(n\) — это количество релевантных элементов в списке.
Сравните с результатами запоминания в точке k .
Б
исходный уровень
Модель, используемая в качестве эталона для сравнения эффективности другой модели (как правило, более сложной). Например, модель логистической регрессии может служить хорошей базовой моделью для глубокой модели .
Для решения конкретной задачи базовый уровень помогает разработчикам моделей количественно оценить минимальную ожидаемую производительность, которую должна достичь новая модель, чтобы быть полезной.
Логические вопросы (BoolQ)
Набор данных для оценки умения студентов магистратуры отвечать на вопросы с вариантами ответа «да» или «нет». Каждое из заданий в наборе данных состоит из трех компонентов:
- Запрос
- Отрывок, подразумевающий ответ на вопрос.
- Правильный ответ — да или нет .
Например:
- Вопрос : Есть ли в Мичигане атомные электростанции?
- Текст : ...три атомные электростанции обеспечивают штат Мичиган примерно 30% его электроэнергии.
- Правильный ответ : Да
Исследователи собрали вопросы из анонимизированных, агрегированных поисковых запросов Google, а затем использовали страницы Википедии для подтверждения полученной информации.
Для получения дополнительной информации см. BoolQ: Изучение удивительной сложности естественных вопросов типа «да/нет» .
BoolQ является компонентом ансамбля SuperGLUE .
BoolQ
Сокращение для логических вопросов .
С
КБ
Сокращенное название CommitmentBank .
F-мера N-граммы символа (ChrF)
Метрика для оценки моделей машинного перевода . Показатель F-меры для N-грамм символов определяет степень перекрытия N-грамм в эталонном тексте с N-граммами в тексте, сгенерированном моделью машинного перевода.
Показатель F-меры для N-грамм символов аналогичен метрикам семейств ROUGE и BLEU , за исключением того, что:
- Показатель F-score для символьных N-грамм применяется к символьным N-граммам.
- ROUGE и BLEU работают с N-граммами или токенами слов .
Выбор правдоподобных альтернатив (COPA)
Набор данных для оценки того, насколько хорошо LLM может определить лучший из двух альтернативных ответов на предпосылку. Каждое из заданий в наборе данных состоит из трех компонентов:
- Предпосылка, которая обычно представляет собой утверждение, за которым следует вопрос.
- На поставленный в предпосылке вопрос можно ответить двумя способами, один из которых верен, а другой неверен.
- Правильный ответ
Например:
- Исходное предположение: Мужчина сломал палец на ноге. В чём причина этого?
- Возможные ответы:
- У него в носке образовалась дырка.
- Он уронил молоток себе на ногу.
- Правильный ответ: 2
COPA является компонентом ансамбля SuperGLUE .
CommitmentBank (CB)
Набор данных для оценки уровня владения студентом магистратуры правом определять, верит ли автор отрывка текста целевому предложению в этом отрывке. Каждая запись в наборе данных содержит:
- Отрывок
- Целевое предложение в этом отрывке
- Логическое значение, указывающее, верит ли автор отрывка целевому предложению.
Например:
- Отрывок: Как же приятно слышать смех Артемиды. Она такая серьёзная девочка. Я и не знала, что у неё есть чувство юмора.
- Целевое условие: у неё было чувство юмора
- Логическое значение : True, что означает, что автор верит целевому предложению.
CommitmentBank является компонентом комплекса SuperGLUE .
КОПА
Сокращение от "Выбор правдоподобных альтернатив" .
расходы
Синоним слова « потеря» .
контрфактуальная справедливость
Метрика справедливости , которая проверяет, дает ли модель классификации одинаковый результат для одного человека и для другого человека, идентичного первому, за исключением одного или нескольких конфиденциальных атрибутов . Оценка модели классификации на предмет контрфактической справедливости — один из методов выявления потенциальных источников предвзятости в модели.
Для получения более подробной информации обратитесь к одному из следующих источников:
- Справедливость: контрфактуальная справедливость в кратком курсе по машинному обучению.
- Когда миры сталкиваются: интеграция различных контрфактических предположений в контексте справедливости
перекрестная энтропия
Обобщение функции логарифмической потери на задачи многоклассовой классификации . Перекрестная энтропия количественно оценивает разницу между двумя распределениями вероятностей. См. также перплексию .
Функция кумулятивного распределения (ФКР)
Функция, определяющая частоту выборок, меньших или равных целевому значению. Например, рассмотрим нормальное распределение непрерывных значений. Функция распределения показывает, что приблизительно 50% выборок должны быть меньше или равны среднему значению, а приблизительно 84% выборок должны быть меньше или равны одному стандартному отклонению выше среднего значения.
Д
демографическое равенство
Показатель справедливости , который считается выполненным, если результаты классификации модели не зависят от заданного конфиденциального атрибута .
Например, если в университет Глуббдубдриба подают заявки как лилипуты, так и бробдингнаги, демографическое равенство достигается, если процент принятых лилипутов совпадает с процентом принятых бробдингнагов, независимо от того, является ли одна группа в среднем более квалифицированной, чем другая.
В отличие от принципов выравнивания шансов и равенства возможностей , которые допускают зависимость результатов классификации в целом от конфиденциальных атрибутов, но не допускают зависимости результатов классификации для определенных заданных эталонных меток от конфиденциальных атрибутов. См. «Борьба с дискриминацией с помощью более интеллектуального машинного обучения» для визуализации, демонстрирующей компромиссы при оптимизации для достижения демографического равенства.
Дополнительную информацию см. в разделе «Справедливость: демографическое равенство» в кратком курсе по машинному обучению.
Е
Расстояние перемещения экскаватора (EMD)
Мера относительного сходства двух распределений . Чем меньше расстояние, пройденное землеройной машиной, тем больше сходство распределений.
расстояние редактирования
Показатель степени сходства двух текстовых строк. В машинном обучении расстояние редактирования полезно по следующим причинам:
- Расстояние редактирования вычислить несложно.
- Функция Edit Distance позволяет сравнивать две строки, заведомо похожие друг на друга.
- Расстояние редактирования может определять степень сходства различных строк с заданной строкой.
Существует несколько определений расстояния редактирования, каждое из которых использует различные строковые операции. Пример можно найти в расстоянии Левенштейна .
эмпирическая кумулятивная функция распределения (eCDF или EDF)
Кумулятивная функция распределения, основанная на эмпирических измерениях из реального набора данных. Значение функции в любой точке вдоль оси x представляет собой долю наблюдений в наборе данных, которые меньше или равны заданному значению.
энтропия
В теории информации энтропия — это описание непредсказуемости распределения вероятностей. В качестве альтернативы, энтропия также определяется как количество информации, содержащейся в каждом примере . Распределение имеет максимально возможную энтропию, когда все значения случайной переменной одинаково вероятны.
Энтропия множества с двумя возможными значениями «0» и «1» (например, метки в задаче бинарной классификации ) имеет следующую формулу:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
где:
- H — это энтропия.
- p — это доля примеров с "1" результатом.
- q — это доля примеров с "0" значениями. Заметим, что q = (1 - p)
- Обычно log равен log 2. В данном случае единицей измерения энтропии является бит.
Например, предположим следующее:
- 100 примеров содержат значение «1»
- В 300 примерах содержится значение «0».
Следовательно, значение энтропии равно:
- p = 0,25
- q = 0,75
- H = (-0,25)log 2 (0,25) - (0,75)log 2 (0,75) = 0,81 бит на пример
Идеально сбалансированный набор (например, 200 нулей и 200 единиц) будет иметь энтропию 1,0 бит на пример. По мере того, как набор становится всё более несбалансированным , его энтропия стремится к 0,0.
В деревьях решений энтропия помогает сформулировать информационный выигрыш , который позволяет алгоритму разделения выбирать условия в процессе построения дерева решений для классификации.
Сравните энтропию с:
- примесь Джини
- функция потерь перекрестной энтропии
Энтропию часто называют энтропией Шеннона .
Для получения дополнительной информации см. раздел «Точный разделитель для бинарной классификации с использованием числовых признаков» в курсе «Лесто решений».
равенство возможностей
Показатель справедливости, позволяющий оценить, насколько хорошо модель предсказывает желаемый результат для всех значений чувствительного атрибута . Другими словами, если желаемый результат для модели — положительный класс , цель состоит в том, чтобы доля истинно положительных результатов была одинаковой для всех групп.
Равенство возможностей связано с выравниванием шансов , что требует, чтобы как показатели истинно положительных результатов, так и показатели ложноположительных результатов были одинаковыми для всех групп.
Предположим, что Университет Глуббдубдриб принимает как лилипутов, так и бробдингнагцев на строгую математическую программу. Средние школы лилипутов предлагают насыщенную программу по математике, и подавляющее большинство учеников соответствуют требованиям для поступления в университет. Средние школы бробдингнагцев вообще не предлагают математических классов, и в результате гораздо меньше их учеников соответствуют требованиям. Равенство возможностей для предпочтительного статуса «принят» в зависимости от национальности (лилипут или бробдингнагец), если вероятность приема квалифицированных студентов одинакова независимо от того, являются ли они лилипутами или бробдингнагцами.
Например, предположим, что 100 лилипутов и 100 бробдингнагцев подают заявления в университет Глуббдубдриб, и решения о приеме принимаются следующим образом:
Таблица 1. Лилипуты среди претендентов (90% соответствуют требованиям)
| Квалифицированный | Неквалифицированный | |
|---|---|---|
| Допущенный | 45 | 3 |
| Отклоненный | 45 | 7 |
| Общий | 90 | 10 |
| Процент принятых студентов, отвечающих требованиям: 45/90 = 50% Процент студентов, не прошедших отбор, составляет 7/10 = 70%. Общий процент принятых студентов-лилипутов: (45+3)/100 = 48% | ||
Таблица 2. Огромное количество претендентов (10% соответствуют требованиям):
| Квалифицированный | Неквалифицированный | |
|---|---|---|
| Допущенный | 5 | 9 |
| Отклоненный | 5 | 81 |
| Общий | 10 | 90 |
| Процент принятых студентов, отвечающих требованиям: 5/10 = 50% Процент студентов, не прошедших отбор, составляет: 81/90 = 90%. Общий процент принятых студентов из Бробдингнага: (5+9)/100 = 14% | ||
Приведенные выше примеры удовлетворяют условию равенства возможностей для приема квалифицированных студентов, поскольку и лилипуты, и бробдингнаги имеют 50%-ный шанс быть принятыми.
Хотя принцип равенства возможностей соблюдается, следующие два показателя справедливости не соблюдаются:
- Демографическое равенство : лилипуты и бробдингнаги поступают в университет с разной частотой; принимается 48% студентов-лилипутов, но только 14% студентов-бробдингнагов.
- Уравненные шансы : Хотя у квалифицированных студентов-лилипутов и студентов-бробдингнагов одинаковые шансы на поступление, дополнительное ограничение, согласно которому у неквалифицированных лилипутов и студентов-бробдингнагов одинаковые шансы на отказ, не выполняется. У неквалифицированных лилипутов процент отказов составляет 70%, а у неквалифицированных студентов-бробдингнагов — 90%.
Дополнительную информацию см. в разделе «Справедливость: равенство возможностей в экспресс-курсе по машинному обучению».
уравненные шансы
Показатель справедливости, позволяющий оценить, насколько хорошо модель прогнозирует результаты для всех значений чувствительного атрибута как для положительного , так и для отрицательного класса, а не только для одного класса в отдельности. Другими словами, как показатель истинно положительных результатов , так и показатель ложноотрицательных результатов должны быть одинаковыми для всех групп.
Принцип выравнивания шансов связан с равенством возможностей , который фокусируется только на частоте ошибок для одного класса (положительного или отрицательного).
Например, предположим, что Университет Глуббдубдриб принимает как лилипутов, так и бробдингнагцев на строгую математическую программу. Средние школы лилипутов предлагают насыщенную программу по математике, и подавляющее большинство учеников соответствуют требованиям для поступления в университет. Средние школы бробдингнагцев вообще не предлагают математических курсов, и в результате гораздо меньше их учеников соответствуют требованиям. Уравненные шансы выполняются при условии, что независимо от того, является ли абитуриент лилипутом или бробдингнагцем, если он соответствует требованиям, у него одинаковая вероятность быть принятым в программу, а если он не соответствует требованиям, у него одинаковая вероятность получить отказ.
Предположим, 100 лилипутов и 100 бробдингнагцев подают заявления в университет Глуббдубдриб, и решения о приеме принимаются следующим образом:
Таблица 3. Лилипуты среди претендентов (90% соответствуют требованиям)
| Квалифицированный | Неквалифицированный | |
|---|---|---|
| Допущенный | 45 | 2 |
| Отклоненный | 45 | 8 |
| Общий | 90 | 10 |
| Процент принятых студентов, отвечающих требованиям: 45/90 = 50% Процент студентов, не прошедших отбор, составляет 8/10 = 80%. Общий процент принятых студентов-лилипутов: (45+2)/100 = 47% | ||
Таблица 4. Огромное количество претендентов (10% соответствуют требованиям):
| Квалифицированный | Неквалифицированный | |
|---|---|---|
| Допущенный | 5 | 18 |
| Отклоненный | 5 | 72 |
| Общий | 10 | 90 |
| Процент принятых студентов, отвечающих требованиям: 5/10 = 50% Процент студентов, не прошедших отбор, составил: 72/90 = 80%. Общий процент принятых студентов из Бробдингнага: (5+18)/100 = 23% | ||
Уравненные шансы соблюдены, поскольку у квалифицированных студентов уровня лилипута и бробдингнага вероятность поступления составляет 50%, а у неквалифицированных студентов уровня лилипута и бробдингнага — 80%.
В работе «Равенство возможностей в контролируемом обучении» формально определяется принцип выравнивания шансов следующим образом: «предиктор Ŷ удовлетворяет принципу выравнивания шансов по отношению к защищаемому атрибуту A и результату Y, если Ŷ и A независимы при условии Y».
оценки
В основном используется как аббревиатура для обозначения оценок в рамках магистерских программ . В более широком смысле, «оценки» — это аббревиатура для любой формы оценки .
оценка
Процесс оценки качества модели или сравнения различных моделей друг с другом.
Для оценки модели машинного обучения с учителем обычно проводят сравнение с проверочным и тестовым наборами данных . Оценка модели машинного обучения с учителем, как правило, включает в себя более широкие оценки качества и безопасности.
точное совпадение
Метрика типа «всё или ничего», при которой выходные данные модели либо точно соответствуют истинным значениям или эталонному тексту , либо нет. Например, если истинные значения — «оранжевый» , то единственным результатом работы модели, удовлетворяющим условию точного совпадения, будет «оранжевый» .
Точное совпадение также может оценивать модели, выходные данные которых представляют собой последовательность (ранжированный список элементов). В общем случае, для точного совпадения требуется, чтобы сгенерированный ранжированный список точно соответствовал истинным значениям; то есть каждый элемент в обоих списках должен быть в одном и том же порядке. Однако, если истинные значения состоят из нескольких правильных последовательностей, то для точного совпадения достаточно, чтобы выходные данные модели совпадали только с одной из правильных последовательностей.
Экстремальное суммирование (xsum)
Набор данных для оценки способности магистра права (LLM) обобщать содержание одного документа. Каждая запись в наборе данных состоит из:
- Документ, подготовленный Британской вещательной корпорацией (BBC).
- Краткое изложение этого документа в одном предложении.
Подробности см. в статье «Не вдавайтесь в подробности, только краткое изложение! Тематически ориентированные сверточные нейронные сети для экстремального суммирования» .
Ф
Ф 1
Сводная метрика бинарной классификации , основанная как на точности , так и на полноте . Вот формула:
метрика справедливости
Математическое определение «справедливости», поддающееся измерению. К числу часто используемых показателей справедливости относятся:
- уравненные шансы
- прогнозируемая паритетность
- контрфактуальная справедливость
- демографическое равенство
Многие показатели справедливости являются взаимоисключающими; см. несовместимость показателей справедливости .
ложноотрицательный результат (FN)
Пример, в котором модель ошибочно предсказывает отрицательный класс . Например, модель предсказывает, что конкретное электронное письмо не является спамом (отрицательный класс), но на самом деле это письмо является спамом .
частота ложноотрицательных результатов
Доля фактически положительных примеров, для которых модель ошибочно предсказала отрицательный класс. Следующая формула вычисляет частоту ложноотрицательных результатов:
Более подробную информацию см. в разделе «Пороги и матрица ошибок» в кратком курсе по машинному обучению.
ложноположительный результат (FP)
Пример, в котором модель ошибочно предсказывает положительный класс . Например, модель предсказывает, что конкретное электронное письмо является спамом (положительный класс), но на самом деле это электронное письмо не является спамом .
Более подробную информацию см. в разделе «Пороги и матрица ошибок» в кратком курсе по машинному обучению.
Частота ложноположительных результатов (FPR)
Доля фактически отрицательных примеров, для которых модель ошибочно предсказала положительный класс. Следующая формула вычисляет частоту ложноположительных результатов:
Показатель ложноположительных результатов отображается по оси X на ROC-кривой .
Дополнительную информацию см. в разделе «Классификация: ROC и AUC в экспресс-курсе по машинному обучению».
важность функций
Синоним переменных важностей .
фундаментальная модель
Очень большая предварительно обученная модель, обученная на огромном и разнообразном обучающем наборе данных . Базовая модель может выполнять обе следующие функции:
- Умеет оперативно реагировать на широкий круг запросов.
- Служит базовой моделью для дальнейшей тонкой настройки или других модификаций.
Иными словами, базовая модель уже в общем смысле очень функциональна, но её можно дополнительно адаптировать, чтобы сделать ещё более полезной для решения конкретной задачи.
доля успехов
Метрика для оценки текста, сгенерированного моделью машинного обучения. Доля успешных результатов — это количество «успешных» сгенерированных текстовых результатов, деленное на общее количество сгенерированных текстовых результатов. Например, если большая языковая модель сгенерировала 10 блоков кода, пять из которых были успешными, то доля успешных результатов составит 50%.
Хотя показатель доли успешных результатов широко используется в статистике, в машинном обучении он в первую очередь полезен для оценки проверяемых задач, таких как генерация кода или решение математических задач.
Г
примесь Джини
Метрика, аналогичная энтропии . Разделители используют значения, полученные либо из коэффициента Джини, либо из энтропии, для составления условий для деревьев решений классификации. Прирост информации выводится из энтропии. Универсально принятого эквивалентного термина для метрики, полученной из коэффициента Джини, не существует; однако эта неназванная метрика так же важна, как и прирост информации.
Коэффициент Джини также называют индексом Джини или просто Джини .
ЧАС
потеря шарнира
Семейство функций потерь для классификации , предназначенных для нахождения границы принятия решения как можно дальше от каждого обучающего примера, тем самым максимизируя расстояние между примерами и границей. KSVM используют функцию потерь типа «шарнир» (или аналогичную функцию, например, квадратичную функцию потерь типа «шарнир»). Для бинарной классификации функция потерь типа «шарнир» определяется следующим образом:
где y — истинная метка, либо -1, либо +1, а y' — исходный результат работы модели классификации :
Следовательно, график зависимости потерь шарнира от (y * y') выглядит следующим образом:
я
несовместимость метрик справедливости
Идея заключается в том, что некоторые понятия справедливости взаимоисключающи и не могут быть удовлетворены одновременно. В результате не существует единой универсальной метрики для количественной оценки справедливости, применимой ко всем задачам машинного обучения.
Хотя это может показаться обескураживающим, несовместимость метрик справедливости не означает, что усилия по обеспечению справедливости бесплодны. Напротив, это говорит о том, что справедливость должна определяться контекстуально для конкретной задачи машинного обучения с целью предотвращения вреда, специфичного для ее вариантов использования.
Более подробное обсуждение несовместимости показателей справедливости см. в разделе "О (не)возможности справедливости" .
индивидуальная справедливость
Показатель справедливости, проверяющий, классифицируются ли похожие люди одинаково. Например, Бробдингнагианская академия может стремиться к обеспечению индивидуальной справедливости, гарантируя, что два студента с одинаковыми оценками и результатами стандартизированных тестов имеют равные шансы на поступление.
Следует отметить, что индивидуальная справедливость полностью зависит от того, как вы определяете «сходство» (в данном случае, оценки и результаты тестов), и вы рискуете столкнуться с новыми проблемами справедливости, если ваш показатель сходства не учитывает важную информацию (например, сложность учебной программы студента).
Более подробное обсуждение индивидуальной справедливости см. в разделе «Справедливость через осведомленность» .
получение информации
В деревьях решений энтропия узла определяется как разница между энтропией узла и взвешенной (по количеству примеров) суммой энтропий его дочерних узлов. Энтропия узла — это энтропия примеров в этом узле.
Например, рассмотрим следующие значения энтропии:
- энтропия родительского узла = 0,6
- Энтропия одного дочернего узла с 16 релевантными примерами = 0,2
- Энтропия другого дочернего узла с 24 релевантными примерами = 0,1
Таким образом, 40% примеров находятся в одном дочернем узле, а 60% — в другом дочернем узле. Следовательно:
- Взвешенная сумма энтропии дочерних узлов = (0,4 * 0,2) + (0,6 * 0,1) = 0,14
Таким образом, прирост информации составляет:
- Прирост информации = энтропия родительского узла - взвешенная сумма энтропий дочерних узлов
- Прирост информации = 0,6 - 0,14 = 0,46
Большинство разделителей стремятся создать условия , которые максимизируют прирост информации.
согласованность между экспертами
Показатель того, насколько часто мнения экспертов-оценщиков совпадают при выполнении задания. Если мнения экспертов расходятся, возможно, необходимо улучшить инструкции к заданию. Иногда также называется межэкспертным согласием или межэкспертной надежностью . См. также коэффициент Каппа Коэна , который является одним из наиболее популярных показателей межэкспертного согласия.
Дополнительную информацию см. в разделе «Категориальные данные: распространенные проблемы в курсе машинного обучения».
Л
Потеря L 1
Функция потерь , которая вычисляет абсолютное значение разницы между фактическими значениями меток и значениями, предсказанными моделью . Например, вот расчет функции потерь L1 для группы из пяти примеров :
| Фактическая ценность примера | Прогнозируемое значение модели | Абсолютное значение дельты |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L 1 потеря | ||
Функция потерь L1 менее чувствительна к выбросам , чем функция потерь L2 .
Средняя абсолютная ошибка — это средняя ошибка L1 на пример.
Дополнительную информацию см. в разделе «Линейная регрессия: функция потерь в машинном обучении» (краткий курс).
Потеря L 2
Функция потерь , которая вычисляет квадрат разницы между фактическими значениями меток и значениями, предсказанными моделью . Например, вот расчет функции потерь L2 для группы из пяти примеров :
| Фактическая ценность примера | Прогнозируемое значение модели | Квадрат дельты |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = L 2 потери | ||
Вследствие возведения в квадрат, функция потерь L2 усиливает влияние выбросов . То есть, функция потерь L2 реагирует на плохие прогнозы сильнее, чем функция потерь L1 . Например, функция потерь L1 для предыдущей партии составила бы 8, а не 16. Обратите внимание, что один выброс объясняет 9 из 16.
В регрессионных моделях в качестве функции потерь обычно используется L2- функция потерь.
Среднеквадратичная ошибка — это средняя ошибка L2 -пространства на пример. Квадратичная ошибка — это другое название ошибки L2 - пространства.
Дополнительную информацию см. в разделе «Логистическая регрессия: функция потерь и регуляризация» в книге «Краткий курс по машинному обучению».
Оценка программ магистратуры в области права (LLM)
Набор метрик и критериев для оценки производительности больших языковых моделей (БЛМ). В общих чертах, оценка БЛМ включает в себя:
- Помогите исследователям выявить области, в которых программы обучения лингвистическим навыкам нуждаются в улучшении.
- Они полезны для сравнения различных моделей обучения и определения наилучшей модели обучения для конкретной задачи.
- Помогите обеспечить безопасность и этичность использования LLM-ов.
See Large language models (LLMs) in Machine Learning Crash Course for more information.
потеря
During the training of a supervised model , a measure of how far a model's prediction is from its label .
A loss function calculates the loss.
See Linear regression: Loss in Machine Learning Crash Course for more information.
функция потерь
During training or testing, a mathematical function that calculates the loss on a batch of examples. A loss function returns a lower loss for models that makes good predictions than for models that make bad predictions.
The goal of training is typically to minimize the loss that a loss function returns.
Many different kinds of loss functions exist. Pick the appropriate loss function for the kind of model you are building. For example:
- L 2 loss (or Mean Squared Error ) is the loss function for linear regression .
- Log Loss is the loss function for logistic regression .
М
матричная факторизация
In math, a mechanism for finding the matrixes whose dot product approximates a target matrix.
In recommendation systems , the target matrix often holds users' ratings on items . For example, the target matrix for a movie recommendation system might look something like the following, where the positive integers are user ratings and 0 means that the user didn't rate the movie:
| Касабланка | The Philadelphia Story | Чёрная Пантера | Чудо-женщина | Криминальное чтиво | |
|---|---|---|---|---|---|
| Пользователь 1 | 5.0 | 3.0 | 0.0 | 2.0 | 0.0 |
| Пользователь 2 | 4.0 | 0.0 | 0.0 | 1.0 | 5.0 |
| Пользователь 3 | 3.0 | 1.0 | 4.0 | 5.0 | 0.0 |
The movie recommendation system aims to predict user ratings for unrated movies. For example, will User 1 like Black Panther ?
One approach for recommendation systems is to use matrix factorization to generate the following two matrixes:
- A user matrix , shaped as the number of users X the number of embedding dimensions.
- An item matrix , shaped as the number of embedding dimensions X the number of items.
For example, using matrix factorization on our three users and five items could yield the following user matrix and item matrix:
User Matrix Item Matrix 1.1 2.3 0.9 0.2 1.4 2.0 1.2 0.6 2.0 1.7 1.2 1.2 -0.1 2.1 2.5 0.5
The dot product of the user matrix and item matrix yields a recommendation matrix that contains not only the original user ratings but also predictions for the movies that each user hasn't seen. For example, consider User 1's rating of Casablanca , which was 5.0. The dot product corresponding to that cell in the recommendation matrix should hopefully be around 5.0, and it is:
(1.1 * 0.9) + (2.3 * 1.7) = 4.9More importantly, will User 1 like Black Panther ? Taking the dot product corresponding to the first row and the third column yields a predicted rating of 4.3:
(1.1 * 1.4) + (2.3 * 1.2) = 4.3Matrix factorization typically yields a user matrix and item matrix that, together, are significantly more compact than the target matrix.
МБПП
Abbreviation for Mostly Basic Python Problems .
Mean Absolute Error (MAE)
The average loss per example when L 1 loss is used. Calculate Mean Absolute Error as follows:
- Calculate the L 1 loss for a batch.
- Divide the L 1 loss by the number of examples in the batch.
For example, consider the calculation of L 1 loss on the following batch of five examples:
| Actual value of example | Model's predicted value | Loss (difference between actual and predicted) |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = L 1 loss | ||
So, L 1 loss is 8 and the number of examples is 5. Therefore, the Mean Absolute Error is:
Mean Absolute Error = L1 loss / Number of Examples Mean Absolute Error = 8/5 = 1.6
Contrast Mean Absolute Error with Mean Squared Error and Root Mean Squared Error .
mean average precision at k (mAP@k)
The statistical mean of all average precision at k scores across a validation dataset. One use of mean average precision at k is to judge the quality of recommendations generated by a recommendation system .
Although the phrase "mean average" sounds redundant, the name of the metric is appropriate. After all, this metric finds the mean of multiple average precision at k values.
Среднеквадратичная ошибка (MSE)
The average loss per example when L 2 loss is used. Calculate Mean Squared Error as follows:
- Calculate the L 2 loss for a batch.
- Divide the L 2 loss by the number of examples in the batch.
For example, consider the loss on the following batch of five examples:
| Фактическая стоимость | Model's prediction | Потеря | Squared loss |
|---|---|---|---|
| 7 | 6 | 1 | 1 |
| 5 | 4 | 1 | 1 |
| 8 | 11 | 3 | 9 |
| 4 | 6 | 2 | 4 |
| 9 | 8 | 1 | 1 |
| 16 = L 2 loss | |||
Therefore, the Mean Squared Error is:
Mean Squared Error = L2 loss / Number of Examples Mean Squared Error = 16/5 = 3.2
Mean Squared Error is a popular training optimizer , particularly for linear regression .
Contrast Mean Squared Error with Mean Absolute Error and Root Mean Squared Error .
TensorFlow Playground uses Mean Squared Error to calculate loss values.
метрика
A statistic that you care about.
An objective is a metric that a machine learning system tries to optimize.
Metrics API (tf.metrics)
A TensorFlow API for evaluating models. For example, tf.metrics.accuracy determines how often a model's predictions match labels.
minimax loss
A loss function for generative adversarial networks , based on the cross-entropy between the distribution of generated data and real data.
Minimax loss is used in the first paper to describe generative adversarial networks.
See Loss Functions in the Generative Adversarial Networks course for more information.
model capacity
The complexity of problems that a model can learn. The more complex the problems that a model can learn, the higher the model's capacity. A model's capacity typically increases with the number of model parameters. For a formal definition of classification model capacity, see VC dimension .
Импульс
A sophisticated gradient descent algorithm in which a learning step depends not only on the derivative in the current step, but also on the derivatives of the step(s) that immediately preceded it. Momentum involves computing an exponentially weighted moving average of the gradients over time, analogous to momentum in physics. Momentum sometimes prevents learning from getting stuck in local minima.
Mostly Basic Python Problems (MBPP)
A dataset for evaluating an LLM's proficiency in generating Python code. Mostly Basic Python Problems provides about 1,000 crowd-sourced programming problems. Each problem in the dataset contains:
- A task description
- Код решения
- Three automated test cases
Н
negative class
In binary classification , one class is termed positive and the other is termed negative . The positive class is the thing or event that the model is testing for and the negative class is the other possibility. For example:
- The negative class in a medical test might be "not tumor."
- The negative class in an email classification model might be "not spam."
Contrast with positive class .
О
цель
A metric that your algorithm is trying to optimize.
целевая функция
The mathematical formula or metric that a model aims to optimize. For example, the objective function for linear regression is usually Mean Squared Loss . Therefore, when training a linear regression model, training aims to minimize Mean Squared Loss.
In some cases, the goal is to maximize the objective function. For example, if the objective function is accuracy, the goal is to maximize accuracy.
See also loss .
П
pass at k (pass@k)
A metric to determine the quality of code (for example, Python) that a large language model generates. More specifically, pass at k tells you the likelihood that at least one generated block of code out of k generated blocks of code will pass all of its unit tests.
Large language models often struggle to generate good code for complex programming problems. Software engineers adapt to this problem by prompting the large language model to generate multiple ( k ) solutions for the same problem. Then, software engineers test each of the solutions against unit tests. The calculation of pass at k depends on the outcome of the unit tests:
- If one or more of those solutions pass the unit test, then the LLM Passes that code generation challenge.
- If none of the solutions pass the unit test, then the LLM Fails that code generation challenge.
The formula for pass at k is as follows:
\[\text{pass at k} = \frac{\text{total number of passes}} {\text{total number of challenges}}\]
In general, higher values of k produce higher pass at k scores; however, higher values of k require more large language model and unit testing resources.
производительность
Overloaded term with the following meanings:
- The standard meaning within software engineering. Namely: How fast (or efficiently) does this piece of software run?
- The meaning within machine learning. Here, performance answers the following question: How correct is this model ? That is, how good are the model's predictions?
permutation variable importances
A type of variable importance that evaluates the increase in the prediction error of a model after permuting the feature's values. Permutation variable importance is a model-independent metric.
недоумение
One measure of how well a model is accomplishing its task. For example, suppose your task is to read the first few letters of a word a user is typing on a phone keyboard, and to offer a list of possible completion words. Perplexity, P, for this task is approximately the number of guesses you need to offer in order for your list to contain the actual word the user is trying to type.
Perplexity is related to cross-entropy as follows:
positive class
The class you are testing for.
For example, the positive class in a cancer model might be "tumor." The positive class in an email classification model might be "spam."
Contrast with negative class .
PR AUC (area under the PR curve)
Area under the interpolated precision-recall curve , obtained by plotting (recall, precision) points for different values of the classification threshold .
точность
A metric for classification models that answers the following question:
When the model predicted the positive class , what percentage of the predictions were correct?
Here is the formula:
где:
- true positive means the model correctly predicted the positive class.
- false positive means the model mistakenly predicted the positive class.
For example, suppose a model made 200 positive predictions. Of these 200 positive predictions:
- 150 were true positives.
- 50 were false positives.
В этом случае:
Contrast with accuracy and recall .
See Classification: Accuracy, recall, precision and related metrics in Machine Learning Crash Course for more information.
precision at k (precision@k)
A metric for evaluating a ranked (ordered) list of items. Precision at k identifies the fraction of the first k items in that list that are "relevant." That is:
\[\text{precision at k} = \frac{\text{relevant items in first k items of the list}} {\text{k}}\]
The value of k must be less than or equal to the length of the returned list. Note that the length of the returned list is not part of the calculation.
Relevance is often subjective; even expert human evaluators often disagree on which items are relevant.
Сравните с:
precision-recall curve
A curve of precision versus recall at different classification thresholds .
prediction bias
A value indicating how far apart the average of predictions is from the average of labels in the dataset.
Not to be confused with the bias term in machine learning models or with bias in ethics and fairness .
predictive parity
A fairness metric that checks whether, for a given classification model , the precision rates are equivalent for subgroups under consideration.
For example, a model that predicts college acceptance would satisfy predictive parity for nationality if its precision rate is the same for Lilliputians and Brobdingnagians.
Predictive parity is sometime also called predictive rate parity .
See "Fairness Definitions Explained" (section 3.2.1) for a more detailed discussion of predictive parity.
predictive rate parity
Another name for predictive parity .
функция плотности вероятности
A function that identifies the frequency of data samples having exactly a particular value. When a dataset's values are continuous floating-point numbers, exact matches rarely occur. However, integrating a probability density function from value x to value y yields the expected frequency of data samples between x and y .
For example, consider a normal distribution having a mean of 200 and a standard deviation of 30. To determine the expected frequency of data samples falling within the range 211.4 to 218.7, you can integrate the probability density function for a normal distribution from 211.4 to 218.7.
Р
Reading Comprehension with Commonsense Reasoning Dataset (ReCoRD)
A dataset to evaluate an LLM's ability to perform commonsense reasoning. Each example in the dataset contains three components:
- A paragraph or two from a news article
- A query in which one of the entities explicitly or implicitly identified in the passage is masked .
- The answer (the name of the entity that belongs in the mask)
See ReCoRD for an extensive list of examples.
ReCoRD is a component of the SuperGLUE ensemble.
RealToxicityPrompts
A dataset that contains a set of sentence beginnings that might contain toxic content. Use this dataset to evaluate an LLM's ability to generate non-toxic text to complete the sentence. Typically, you use the Perspective API to determine how well the LLM performed at this task.
See RealToxicityPrompts: Evaluating Neural Toxic Degeneration in Language Models for details.
отзывать
A metric for classification models that answers the following question:
When ground truth was the positive class , what percentage of predictions did the model correctly identify as the positive class?
Here is the formula:
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
где:
- true positive means the model correctly predicted the positive class.
- false negative means that the model mistakenly predicted the negative class .
For instance, suppose your model made 200 predictions on examples for which ground truth was the positive class. Of these 200 predictions:
- 180 were true positives.
- 20 were false negatives.
В этом случае:
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
See Classification: Accuracy, recall, precision and related metrics for more information.
recall at k (recall@k)
A metric for evaluating systems that output a ranked (ordered) list of items. Recall at k identifies the fraction of relevant items in the first k items in that list out of the total number of relevant items returned.
\[\text{recall at k} = \frac{\text{relevant items in first k items of the list}} {\text{total number of relevant items in the list}}\]
Contrast with precision at k .
Recognizing Textual Entailment (RTE)
A dataset for evaluating an LLM's ability to determine whether a hypothesis can be entailed (logically drawn) from a text passage. Each example in an RTE evaluation consists of three parts:
- A passage, typically from news or Wikipedia articles
- A hypothesis
- The correct answer, which is either:
- True, meaning the hypothesis can be entailed from the passage
- False, meaning the hypothesis can't be entailed from the passage
Например:
- Passage: The Euro is the currency of the European Union.
- Hypothesis: France uses the Euro as currency.
- Entailment: True, because France is part of the European Union.
RTE is a component of the SuperGLUE ensemble.
Записывать
Abbreviation for Reading Comprehension with Commonsense Reasoning Dataset .
ROC (receiver operating characteristic) Curve
A graph of true positive rate versus false positive rate for different classification thresholds in binary classification.
The shape of an ROC curve suggests a binary classification model's ability to separate positive classes from negative classes. Suppose, for example, that a binary classification model perfectly separates all the negative classes from all the positive classes:
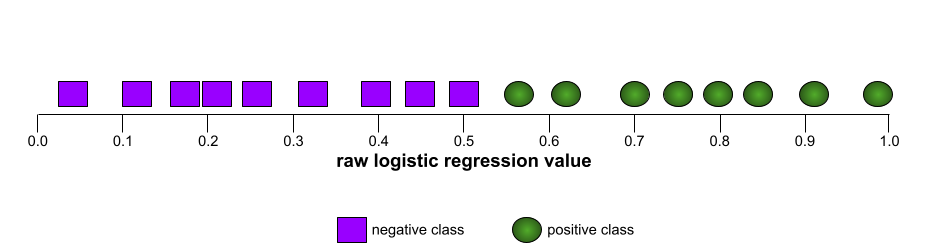
The ROC curve for the preceding model looks as follows:
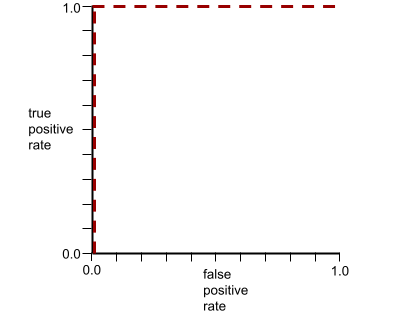
In contrast, the following illustration graphs the raw logistic regression values for a terrible model that can't separate negative classes from positive classes at all:
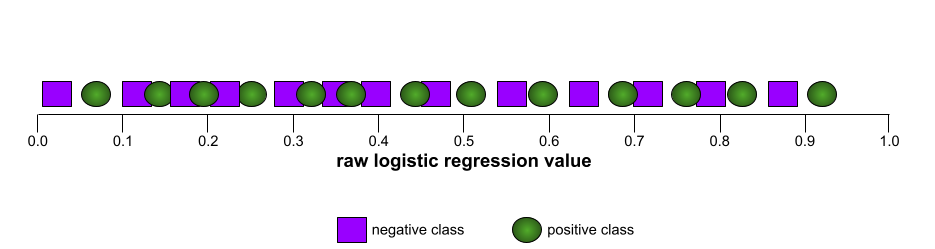
The ROC curve for this model looks as follows:
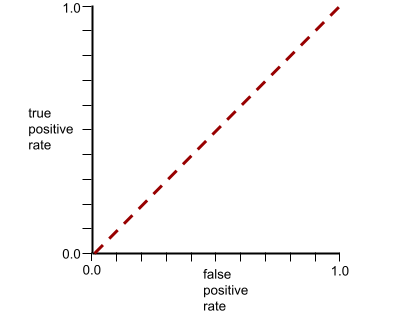
Meanwhile, back in the real world, most binary classification models separate positive and negative classes to some degree, but usually not perfectly. So, a typical ROC curve falls somewhere between the two extremes:
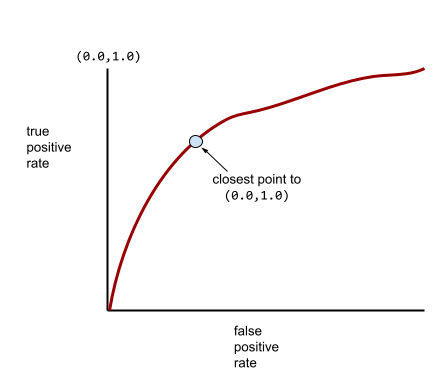
The point on an ROC curve closest to (0.0,1.0) theoretically identifies the ideal classification threshold. However, several other real-world issues influence the selection of the ideal classification threshold. For example, perhaps false negatives cause far more pain than false positives.
A numerical metric called AUC summarizes the ROC curve into a single floating-point value.
Root Mean Squared Error (RMSE)
The square root of the Mean Squared Error .
ROUGE (Recall-Oriented Understudy for Gisting Evaluation)
A family of metrics that evaluate automatic summarization and machine translation models. ROUGE metrics determine the degree to which a reference text overlaps an ML model's generated text . Each member of the ROUGE family measures overlap in a different way. Higher ROUGE scores indicate more similarity between the reference text and generated text than lower ROUGE scores.
Each ROUGE family member typically generates the following metrics:
- Точность
- Отзывать
- Ф 1
For details and examples, see:
РУЖ-Л
A member of the ROUGE family focused on the length of the longest common subsequence in the reference text and generated text . The following formulas calculate recall and precision for ROUGE-L:
You can then use F 1 to roll up ROUGE-L recall and ROUGE-L precision into a single metric:
ROUGE-L ignores any newlines in the reference text and generated text, so the longest common subsequence could cross multiple sentences. When the reference text and generated text involve multiple sentences, a variation of ROUGE-L called ROUGE-Lsum is generally a better metric. ROUGE-Lsum determines the longest common subsequence for each sentence in a passage and then calculates the mean of those longest common subsequences.
ROUGE-N
A set of metrics within the ROUGE family that compares the shared N-grams of a certain size in the reference text and generated text . For example:
- ROUGE-1 measures the number of shared tokens in the reference text and generated text.
- ROUGE-2 measures the number of shared bigrams (2-grams) in the reference text and generated text.
- ROUGE-3 measures the number of shared trigrams (3-grams) in the reference text and generated text.
You can use the following formulas to calculate ROUGE-N recall and ROUGE-N precision for any member of the ROUGE-N family:
You can then use F 1 to roll up ROUGE-N recall and ROUGE-N precision into a single metric:
ROUGE-S
A forgiving form of ROUGE-N that enables skip-gram matching. That is, ROUGE-N only counts N-grams that match exactly , but ROUGE-S also counts N-grams separated by one or more words. For example, consider the following:
- reference text : White clouds
- generated text : White billowing clouds
When calculating ROUGE-N, the 2-gram, White clouds doesn't match White billowing clouds . However, when calculating ROUGE-S, White clouds does match White billowing clouds .
R-squared
A regression metric indicating how much variation in a label is due to an individual feature or to a feature set. R-squared is a value between 0 and 1, which you can interpret as follows:
- An R-squared of 0 means that none of a label's variation is due to the feature set.
- An R-squared of 1 means that all of a label's variation is due to the feature set.
- An R-squared between 0 and 1 indicates the extent to which the label's variation can be predicted from a particular feature or the feature set. For example, an R-squared of 0.10 means that 10 percent of the variance in the label is due to the feature set, an R-squared of 0.20 means that 20 percent is due to the feature set, and so on.
R-squared is the square of the Pearson correlation coefficient between the values that a model predicted and ground truth .
РТЭ
Abbreviation for Recognizing Textual Entailment .
С
подсчет очков
The part of a recommendation system that provides a value or ranking for each item produced by the candidate generation phase.
similarity measure
In clustering algorithms, the metric used to determine how alike (how similar) any two examples are.
sparsity
The number of elements set to zero (or null) in a vector or matrix divided by the total number of entries in that vector or matrix. For example, consider a 100-element matrix in which 98 cells contain zero. The calculation of sparsity is as follows:
Feature sparsity refers to the sparsity of a feature vector; model sparsity refers to the sparsity of the model weights.
Отряд
Acronym for Stanford Question Answering Dataset , introduced in the paper SQuAD: 100,000+ Questions for Machine Comprehension of Text . The questions in this dataset come from people posing questions about Wikipedia articles. Some of the questions in SQuAD have answers, but other questions intentionally don't have answers. Therefore, you can use SQuAD to evaluate an LLM's ability to do both of the following:
- Answer questions that can be answered.
- Identify questions that cannot be answered.
Exact match in combination with F 1 are the most common metrics for evaluating LLMs against SQuAD.
squared hinge loss
The square of the hinge loss . Squared hinge loss penalizes outliers more harshly than regular hinge loss.
squared loss
Synonym for L 2 loss .
SuperGLUE
An ensemble of datasets for rating an LLM's overall ability to understand and generate text. The ensemble consists of the following datasets:
- Boolean Questions (BoolQ)
- CommitmentBank (CB)
- Choice of Plausible Alternatives (COPA)
- Multi-sentence Reading Comprehension (MultiRC)
- Reading Comprehension with Commonsense Reasoning Dataset (ReCoRD)
- Recognizing Textual Entailment (RTE)
- Words in Context (WiC)
- Winograd Schema Challenge (WSC)
For details, see SuperGLUE: A Stickier Benchmark for General-Purpose Language Understanding Systems .
Т
test loss
A metric representing a model's loss against the test set . When building a model , you typically try to minimize test loss. That's because a low test loss is a stronger quality signal than a low training loss or low validation loss .
A large gap between test loss and training loss or validation loss sometimes suggests that you need to increase the regularization rate .
top-k accuracy
The percentage of times that a "target label" appears within the first k positions of generated lists. The lists could be personalized recommendations or a list of items ordered by softmax .
Top-k accuracy is also known as accuracy at k .
токсичность
The degree to which content is abusive, threatening, or offensive. Many machine learning models can identify, measure, and classify toxicity. Most of these models identify toxicity along multiple parameters, such as the level of abusive language and the level of threatening language.
training loss
A metric representing a model's loss during a particular training iteration. For example, suppose the loss function is Mean Squared Error . Perhaps the training loss (the Mean Squared Error) for the 10th iteration is 2.2, and the training loss for the 100th iteration is 1.9.
A loss curve plots training loss versus the number of iterations. A loss curve provides the following hints about training:
- A downward slope implies that the model is improving.
- An upward slope implies that the model is getting worse.
- A flat slope implies that the model has reached convergence .
For example, the following somewhat idealized loss curve shows:
- A steep downward slope during the initial iterations, which implies rapid model improvement.
- A gradually flattening (but still downward) slope until close to the end of training, which implies continued model improvement at a somewhat slower pace then during the initial iterations.
- A flat slope towards the end of training, which suggests convergence.
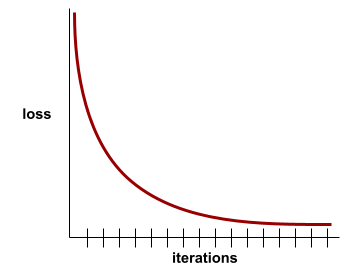
Although training loss is important, see also generalization .
Trivia Question Answering
Datasets to evaluate an LLM's ability to answer trivia questions. Each dataset contains question-answer pairs authored by trivia enthusiasts. Different datasets are grounded by different sources, including:
- Web search (TriviaQA)
- Wikipedia (TriviaQA_wiki)
For more information see TriviaQA: A Large Scale Distantly Supervised Challenge Dataset for Reading Comprehension .
true negative (TN)
An example in which the model correctly predicts the negative class . For example, the model infers that a particular email message is not spam , and that email message really is not spam .
true positive (TP)
An example in which the model correctly predicts the positive class . For example, the model infers that a particular email message is spam, and that email message really is spam.
true positive rate (TPR)
Synonym for recall . That is:
True positive rate is the y-axis in an ROC curve .
Typologically Diverse Question Answering (TyDi QA)
A large dataset for evaluating an LLM's proficiency in answering questions. The dataset contains question and answer pairs in many languages.
For details, see TyDi QA: A Benchmark for Information-Seeking Question Answering in Typologically Diverse Languages .
В
validation loss
A metric representing a model's loss on the validation set during a particular iteration of training.
See also generalization curve .
variable importances
A set of scores that indicates the relative importance of each feature to the model.
For example, consider a decision tree that estimates house prices. Suppose this decision tree uses three features: size, age, and style. If a set of variable importances for the three features are calculated to be {size=5.8, age=2.5, style=4.7}, then size is more important to the decision tree than age or style.
Different variable importance metrics exist, which can inform ML experts about different aspects of models.
В
Wasserstein loss
One of the loss functions commonly used in generative adversarial networks , based on the earth mover's distance between the distribution of generated data and real data.
WiC
Abbreviation for Words in Context .
WikiLingua (wiki_lingua)
A dataset for evaluating an LLM's ability to summarize short articles. WikiHow , an encyclopedia of articles explaining how to do various tasks, is the human-authored source for both the articles and the summaries. Each entry in the dataset consists of:
- An article, which is created by appending each step of the prose (paragraph) version of the numbered list, minus the opening sentence of each step.
- A summary of that article, consisting of the opening sentence of each step in the numbered list.
For details, see WikiLingua: A New Benchmark Dataset for Cross-Lingual Abstractive Summarization .
Winograd Schema Challenge (WSC)
A format (or dataset conforming to that format) for evaluating an LLM's ability to determine the noun phrase that a pronoun refers to.
Each entry in a Winograd Schema Challenge consists of:
- A short passage, which contains a target pronoun
- A target pronoun
- Candidate noun phrases, followed by the correct answer (a Boolean). If the target pronoun refers to this candidate, the answer is True. If the target pronoun does not refer to this candidate, the answer is False.
Например:
- Passage : Mark told Pete many lies about himself, which Pete included in his book. He should have been more truthful.
- Target pronoun : He
- Candidate noun phrases :
- Mark: True, because the target pronoun refers to Mark
- Pete: False, because the target pronoun doesn't refer to Peter
The Winograd Schema Challenge is a component of the SuperGLUE ensemble.
Words in Context (WiC)
A dataset for evaluating how well an LLM uses context to understand words that have multiple meanings. Each entry in the dataset contains:
- Two sentences, each containing the target word
- The target word
- The correct answer (a Boolean), where:
- True means the target word has the same meaning in the two sentences
- False means the target word has a different meaning in the two sentences
Например:
- Two sentences:
- There's a lot of trash on the bed of the river.
- I keep a glass of water next to my bed when I sleep.
- The target word: bed
- Correct answer : False, because the target word has a different meaning in the two sentences.
For details, see WiC: the Word-in-Context Dataset for Evaluating Context-Sensitive Meaning Representations .
Words in Context is a component of the SuperGLUE ensemble.
WSC
Abbreviation for Winograd Schema Challenge .
X
XL-Sum (xlsum)
A dataset for evaluating an LLM's proficiency in summarizing text. XL-Sum provides entries in many languages. Each entry in the dataset contains:
- An article, taken from the British Broadcasting Company (BBC).
- A summary of the article, written by the article's author. Note that that summary can contain words or phrases not present in the article.
For details, see XL-Sum: Large-Scale Multilingual Abstractive Summarization for 44 Languages .