Questa pagina contiene i termini del glossario dei modelli di immagine. Per tutti i termini del glossario, fai clic qui.
A
realtà aumentata
Una tecnologia che sovrappone un'immagine generata da computer a una vista dell'utente del mondo reale, fornendo così una vista composita.
encoder automatico
È un sistema che impara a estrarre le informazioni più importanti dall'input. Gli autoencoder sono una combinazione di encoder e decoder. I codificatori automatici si basano sulla seguente procedura in due fasi:
- L'encoder mappa l'input a un formato (di solito) con dimensioni inferiori (intermedie) con perdita di dati.
- Il decoder crea una versione con perdita dell'input originale mappando il formato di dimensione inferiore al formato di input originale con dimensione superiore.
I codificatori automatici vengono addestrati end-to-end facendo in modo che il decoder tenti di ricostruire il più fedelmente possibile l'input originale dal formato intermedio dell'encoder. Poiché il formato intermedio è più piccolo (dimensione inferiore) rispetto al formato originale, l'autoencoder deve imparare quali informazioni nell'input sono essenziali e l'output non sarà perfettamente identico all'input.
Ad esempio:
- Se i dati di input sono grafici, la copia non esatta sarebbe simile alla grafica originale, ma in qualche modo modificata. Può darsi che una copia non esatta rimuova il rumore dalla grafica originale o riempia alcuni pixel mancanti.
- Se i dati di input sono testo, un encoder automatico genererà un nuovo testo che mimiti (ma non è identico) il testo originale.
Vedi anche autoencoder variazionali.
modello autoregressivo
Un model che deduce una previsione in base alle proprie previsioni precedenti. Ad esempio, i modelli linguistici autoregressivi prevedono il token successivo in base ai token previsti in precedenza. Tutti i modelli linguistici di grandi dimensioni basati su Transformer sono regressivi.
Al contrario, i modelli di immagine basati su GAN di solito non sono autoregressivi poiché generano un'immagine in un singolo passaggio in avanti e non in modo iterativo. Tuttavia, alcuni modelli di generazione di immagini sono regressivi perché generano un'immagine in passaggi.
B
riquadro di delimitazione
In un'immagine, le coordinate (x, y) di un rettangolo intorno a un'area di interesse, ad esempio il cane nell'immagine di seguito.

C
convoluzione
In matematica, casualmente, è una combinazione di due funzioni. Nel machine learning, una convoluzione mescola il filtro convoluzionale e la matrice di input per addestrare le ponderazioni.
Il termine "convoluzione" nel machine learning rappresenta spesso un modo abbreviato per fare riferimento all'operazione convoluzionale o al livello convoluzionale.
Senza le convoluzioni, un algoritmo di machine learning dovrebbe apprendere un peso separato per ogni cella in un tensore di grandi dimensioni. Ad esempio, un addestramento di un algoritmo di machine learning su immagini 2000 x 2000 sarebbe costretto a trovare 4 milioni di pesi separati. Grazie alle convoluzioni, un algoritmo di machine learning deve trovare solo le ponderazioni per ogni cella del filtro convoluzionale, riducendo drasticamente la memoria necessaria per l'addestramento del modello. Quando viene applicato il filtro convoluzionale, viene semplicemente replicato tra le celle in modo che ciascuna venga moltiplicata per il filtro.
filtro convoluzionale
Uno dei due attori in un' operazione convoluzionale. (L'altro attore è una sezione di una matrice di input.) Un filtro convoluzionale è una matrice con lo stesso ranking della matrice di input, ma una forma più piccola. Ad esempio, data una matrice di input 28 x 28, il filtro potrebbe essere qualsiasi matrice 2D più piccola di 28 x 28.
Nella manipolazione fotografica, tutte le celle di un filtro convoluzionale sono generalmente impostate su un modello costante di uno e zeri. Nel machine learning, i filtri convoluzionali vengono generalmente sottoposti a seeding con numeri casuali e quindi la rete addestra i valori ideali.
livello convoluzionale
Livello di una rete neurale profonda in cui un filtro convoluzionale passa lungo una matrice di input. Ad esempio, considera il seguente filtro convoluzionale 3x3:
![Una matrice 3x3 con i seguenti valori: [[0,1,0], [1,0,1], [0,1,0]]](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalFilter33.svg?authuser=2&hl=it)
L'animazione seguente mostra un livello convoluzionale composto da 9 operazioni convoluzionali che coinvolgono la matrice di input 5x5. Nota che ogni operazione convoluzionale funziona su una sezione 3x3 diversa della matrice di input. La matrice 3 x 3 risultante (a destra) è composta dai risultati delle 9 operazioni convoluzionali:
![Un'animazione che mostra due matrici. La prima matrice è la matrice 5x5: [[128,97,53,201,198], [35,22,25,200,195],
[37,24,28,197,182], [33,28,92,195,179], [10,1,7,40]
La seconda matrice è la matrice 3x3:
[[181.303.618], [115.338.605], [169.351.560]].
La seconda matrice viene calcolata applicando il filtro
convoluzionale [[0, 1, 0], [1, 0, 1], [0, 1, 0]] su
diversi sottoinsiemi 3x3 della matrice 5x5.](https://developers.google.com/static/machine-learning/glossary/images/AnimatedConvolution.gif?authuser=2&hl=it)
rete neurale convoluzionale
Una rete neurale in cui almeno un livello è un livello convoluzionale. Una tipica rete neurale convoluzionale è composta da una combinazione dei seguenti livelli:
Le reti neurali convoluzionali si sono rivelate molto efficaci in alcuni tipi di problemi, come il riconoscimento delle immagini.
operazione convoluzionale
La seguente operazione matematica in due fasi:
- Moltiplicazione per elemento del filtro convoluzionale e di una sezione di una matrice di input. (La sezione della matrice di input ha lo stesso ranking e la stessa dimensione del filtro convoluzionale.)
- Somma di tutti i valori nella matrice dei prodotti risultante.
Ad esempio, considera la seguente matrice di input 5 x 5:
![La matrice 5x5: [[128,97,53,201,198], [35,22,25,200,195],
[37,24,28,197,182], [33,28,92,195,179], [31,40,2,100,1]](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerInputMatrix.svg?authuser=2&hl=it)
Ora immagina il seguente filtro convoluzionale 2 x 2:
![La matrice 2x2: [[1, 0], [0, 1]]](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerFilter.svg?authuser=2&hl=it)
Ogni operazione convoluzionale prevede una singola sezione 2 x 2 della matrice di input. Ad esempio, supponiamo di utilizzare la sezione 2 x 2 in alto a sinistra della matrice di input. Quindi, l'operazione di convoluzione su questa sezione è la seguente:
![Applicando il filtro convoluzionale [[1, 0], [0, 1]] alla sezione 2x2 in alto a sinistra della matrice di input, che è [[128,97], [35,22]].
Il filtro convoluzionale lascia intatti i numeri 128 e 22, azzerando i numeri 97 e 35. Di conseguenza, l'operazione di convoluzione restituisce il valore 150 (128+22).](https://developers.google.com/static/machine-learning/glossary/images/ConvolutionalLayerOperation.svg?authuser=2&hl=it)
Un livello convoluzionale è costituito da una serie di operazioni convoluzionali, ognuna delle quali agisce su una sezione diversa della matrice di input.
D
aumento dei dati
È possibile aumentare in modo artificiale l'intervallo e il numero di esempi di addestramento trasformando gli esempi esistenti in modo da crearne altri. Ad esempio, supponiamo che le immagini siano una delle tue caratteristiche, ma il tuo set di dati non contiene abbastanza esempi di immagini per consentire al modello di apprendere associazioni utili. Idealmente, dovresti aggiungere al set di dati un numero sufficiente di immagini etichettate per consentire al modello di eseguire correttamente l'addestramento. Se ciò non è possibile, l'aumento dei dati può ruotare, allungare e riflettere ogni immagine per produrre molte varianti dell'immagine originale, producendo possibilmente dati etichettati sufficienti per consentire un addestramento eccellente.
Rete neurale convoluzionale separabile in profondità (sepCNN)
Un'architettura di rete neurale convoluzionale basata su Inception, ma in cui i moduli Inception vengono sostituiti da convoluzioni separabili in profondità. È anche noto come Xception.
Una convoluzione separabile in profondità (abbreviata anche come convoluzione separabile) fattoria una convoluzione 3D standard in due operazioni di convoluzione separate più efficienti dal punto di vista computazionale: prima una convoluzione di profondità, con una profondità di 1 (n x n x 1), e poi una convoluzione a punto, con lunghezza x n larghezza di 1 (1 x n).
Per scoprire di più, consulta Xception: deep learning con convoluzioni separate in profondità.
sottocampionamento
Termine sovraccarico che può indicare una delle seguenti situazioni:
- Ridurre la quantità di informazioni in una funzionalità per addestrare un modello in modo più efficiente. Ad esempio, prima di addestrare un modello di riconoscimento delle immagini, sottocampionando le immagini ad alta risoluzione a un formato a risoluzione più bassa.
- Addestramento su una percentuale sproporzionatamente bassa di esempi di classi sovrarappresentati per migliorare l'addestramento del modello nelle classi sottorappresentate. Ad esempio, in un set di dati con squilibrio tra le classi, i modelli tendono a imparare molto sulla classe di maggioranza e non abbastanza sulla classe di minoranza. Il sottocampionamento aiuta a bilanciare la quantità di addestramento per le classi di maggioranza e di minoranza.
F
messa a punto
Un secondo pass di addestramento specifico per l'attività eseguito su un modello preaddestrato per perfezionare i parametri in base a un caso d'uso specifico. Ad esempio, la sequenza completa di addestramento per alcuni modelli linguistici di grandi dimensioni è la seguente:
- Preaddestramento: addestra un modello linguistico di grandi dimensioni (LLM) su un ampio set di dati generale, ad esempio tutte le pagine di Wikipedia in lingua inglese.
- Ottimizzazione: addestra il modello preaddestrato per eseguire un'attività specifica, ad esempio rispondere a domande mediche. Il perfezionamento comporta in genere centinaia o migliaia di esempi incentrati sull'attività specifica.
Ecco un altro esempio: la sequenza completa di addestramento per un modello con immagini di grandi dimensioni è la seguente:
- Preaddestramento: addestra un modello di immagini di grandi dimensioni su un vasto set di dati di immagini generali, come tutte le immagini in Wikimedia Commons.
- Perfezionamento: addestra il modello preaddestrato per eseguire un'attività specifica, ad esempio la generazione di immagini di orche.
Il perfezionamento può comportare una combinazione delle seguenti strategie:
- Modifica di tutti i parametri esistenti del modello preaddestrato. Questa procedura è a volte chiamata ottimizzazione completa.
- Modificare solo alcuni dei parametri esistenti del modello preaddestrato (in genere, i livelli più vicini al livello di output), senza modificare gli altri parametri esistenti (in genere quelli più vicini al livello di input). Consulta l'ottimizzazione efficiente dei parametri.
- Aggiunta di altri livelli, in genere sopra quelli esistenti più vicini al livello di output.
Il perfezionamento è una forma di Transfer Learning. Di conseguenza, l'ottimizzazione potrebbe utilizzare una funzione di perdita o un tipo di modello diverso rispetto a quelli utilizzati per addestrare il modello preaddestrato. Ad esempio, potresti perfezionare un modello di immagini di grandi dimensioni preaddestrato per produrre un modello di regressione che restituisca il numero di uccelli in un'immagine di input.
Metti a confronto i seguenti termini di messa a punto:
G
IA generativa
Un campo rivoluzionario emergente senza una definizione formale. Detto questo, la maggior parte degli esperti concorda sul fatto che i modelli di IA generativa possono creare ("generare") contenuti che corrispondono a quanto segue:
- complesso
- coerente
- originale
Ad esempio, un modello di IA generativa può creare immagini o saggi.
Anche alcune tecnologie precedenti, tra cui gli LSTM e gli RNN, possono generare contenuti originali e coerenti. Alcuni esperti considerano queste tecnologie precedenti come IA generativa, mentre altri ritengono che la vera IA generativa richieda risultati più complessi rispetto a quelli prodotti dalle tecnologie precedenti.
Sono invece opposti al ML predittivo.
I
riconoscimento immagine
Un processo che classifica gli oggetti, i pattern o i concetti in un'immagine. Il riconoscimento delle immagini è anche noto come classificazione delle immagini.
Per maggiori informazioni, consulta ML Practicum: Image Classification.
intersezione su unione (IoU)
L'intersezione di due insiemi divisa per la relativa unione. Nelle attività di rilevamento delle immagini di machine learning, l'IoU viene utilizzata per misurare l'accuratezza del riquadro di delimitazione previsto del modello in relazione al riquadro di delimitazione dati empirici reali. In questo caso, l'IoU dei due riquadri è il rapporto tra l'area in sovrapposizione e l'area totale e il suo valore va da 0 (nessuna sovrapposizione del riquadro di delimitazione previsto e del riquadro di delimitazione dei dati empirici reali) a 1 (il riquadro di delimitazione previsto e il riquadro di delimitazione dei dati empirici reali hanno le stesse coordinate).
Ad esempio, nell'immagine di seguito:
- Il riquadro di delimitazione previsto (le coordinate che definiscono il punto in cui il modello prevede la posizione del tavolino nel dipinto) è contorto in viola.
- Il riquadro di delimitazione dei dati empirici reali (le coordinate che definiscono il punto in cui si trova effettivamente la tabella notturna nel quadro) è contornato in verde.
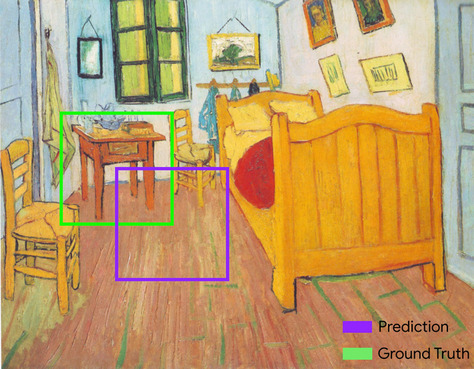
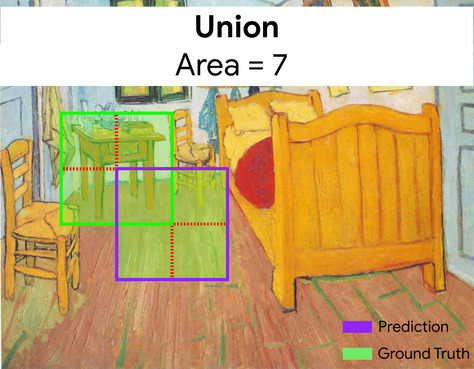
In questo caso, l'intersezione dei riquadri di delimitazione per la previsione e i dati empirici reali (in basso a sinistra) è 1 e l'unione dei riquadri di delimitazione per la previsione e i dati empirici reali (in basso a destra) è 7, quindi l'IoU è \(\frac{1}{7}\).

K
punti chiave
Le coordinate di particolari elementi in un'immagine. Ad esempio, per un modello di riconoscimento delle immagini in grado di distinguere le specie di fiori, i punti chiave potrebbero essere il centro di ogni petalo, lo stelo, lo stame e così via.
L
punti di riferimento
Sinonimo di keypoints.
L
MNIST
Un set di dati di dominio pubblico compilato da LeCun, Cortes e Burges contenente 60.000 immagini, ciascuna delle quali mostra come una persona ha scritto manualmente una determinata cifra da 0 a 9. Ogni immagine è archiviata come array di numeri interi 28 x 28, dove ogni numero intero corrisponde a un valore in scala di grigi compreso tra 0 e 255 inclusi.
MNIST è un set di dati canonico per il machine learning, spesso utilizzato per testare nuovi approcci di machine learning. Per maggiori dettagli, consulta il documento MNIST Database of Handwrites.
P
pooling
Ridurre una o più matrici create da un livello convoluzionale precedente in una matrice più piccola. Il pooling solitamente comporta l'applicazione del valore massimo o medio all'interno dell'area complessiva. Supponiamo, ad esempio, di avere la seguente matrice 3 x 3:
![La matrice 3x3 [[5,3,1], [8,2,5], [9,4,3]].](https://developers.google.com/static/machine-learning/glossary/images/PoolingStart.svg?authuser=2&hl=it)
Un'operazione di pooling, proprio come un'operazione convoluzionale, divide la matrice in sezioni e poi fa scorrere l'operazione convoluzionale di passi. Ad esempio, supponiamo che l'operazione di pool divisi la matrice convoluzionale in sezioni 2x2 con un passo di 1x1. Come illustrato nel seguente diagramma, si svolgono quattro operazioni di pooling. Immagina che ogni operazione di pooling scelga il valore massimo dei quattro in quella sezione:
![La matrice di input è 3x3 con i valori: [[5,3,1], [8,2,5], [9,4,3]].
La sottomatrice 2x2 in alto a sinistra della matrice di input è [[5,3], [8,2]], quindi
l'operazione di pooling in alto a sinistra restituisce il valore 8 (che è il
massimo di 5, 3, 8 e 2). La sottomatrice 2x2 in alto a destra della matrice di input è [[3,1], [2,5]], quindi l'operazione di pooling in alto a destra restituisce il
valore 5. La sottomatrice 2x2 in basso a sinistra della matrice di input è [[8,2], [9,4]], quindi l'operazione di pooling in basso a sinistra restituisce il valore
9. La sottomatrice 2x2 in basso a destra della matrice di input è [[2,5], [4,3]], quindi l'operazione di pooling in basso a destra restituisce il valore
5. Riassumendo, l'operazione di pooling restituisce la matrice 2x2
[[8,5], [9,5]].](https://developers.google.com/static/machine-learning/glossary/images/PoolingConvolution.svg?authuser=2&hl=it)
Il pooling consente di applicare l'invarianza di traduzione nella matrice di input.
Il pooling per le applicazioni di visione artificiale è noto formalmente come pooling spaziale. In genere, per le applicazioni delle serie temporali si fa riferimento al pooling come pool temporale. Meno formalmente, il pooling viene spesso chiamato sottocampionamento o downcampionamento.
modello preaddestrato
Modelli o componenti del modello (come un vettore di incorporamento) già addestrati. A volte, invii vettori di incorporamento preaddestrati in una rete neurale. Altre volte, il modello addestrerà i vettori di incorporamento in sé, invece di affidarsi agli incorporamenti preaddestrati.
Il termine modello linguistico preaddestrato fa riferimento a un modello linguistico di grandi dimensioni (LLM) che è stato sottoposto a preaddestramento.
preaddestramento
L'addestramento iniziale di un modello su un grande set di dati. Alcuni modelli preaddestrati sono giganti e in genere devono essere perfezionati mediante addestramento aggiuntivo. Ad esempio, gli esperti di ML potrebbero preaddestrare un modello linguistico di grandi dimensioni (LLM) su un vasto set di dati di testo, come tutte le pagine in inglese su Wikipedia. Dopo il pre-addestramento, il modello risultante potrebbe essere ulteriormente perfezionato tramite una delle seguenti tecniche:
- distillazione
- ottimizzazione
- ottimizzazione delle istruzioni
- ottimizzazione efficiente dei parametri
- ottimizzazione dei prompt
R
invarianza rotazionale
In un problema di classificazione delle immagini, la capacità di un algoritmo di classificare correttamente le immagini anche quando cambia l'orientamento dell'immagine. Ad esempio, l'algoritmo è comunque in grado di identificare una racchetta da tennis se punta in alto, in posizione orizzontale o in basso. Tieni presente che l'invarianza rotazionale non è sempre desiderabile; ad esempio, un 9 capovolto non deve essere classificato come 9.
Vedi anche invarianza della traduzione e invarianza delle dimensioni.
S
invarianza delle dimensioni
In un problema di classificazione delle immagini, la capacità di un algoritmo di classificare correttamente le immagini anche quando le dimensioni delle immagini cambiano. Ad esempio, l'algoritmo è comunque in grado di identificare un gatto se consuma 2 milioni di pixel o 200.000 pixel. Tieni presente che anche i migliori algoritmi di classificazione delle immagini hanno ancora limiti pratici di invarianza delle dimensioni. Ad esempio, è improbabile che un algoritmo (o un essere umano) classifichi correttamente un'immagine di gatto che consuma solo 20 pixel.
Vedi anche invarianza della traduzione e invarianza rotazionale.
pooling spaziale
Consulta la sezione pooling.
stride
In un'operazione convoluzionale o un pooling, il delta in ogni dimensione della prossima serie di sezioni di input. Ad esempio, l'animazione seguente mostra un passo (1,1) durante un'operazione convoluzionale. Di conseguenza, la sezione di input successiva inizia una posizione a destra della sezione di input precedente. Quando l'operazione raggiunge il bordo destro, la sezione successiva è completamente a sinistra, ma una posizione verso il basso.
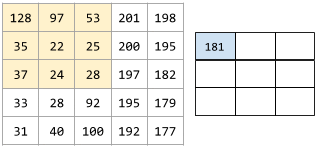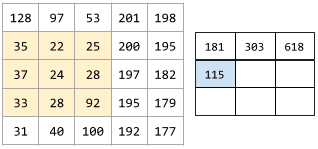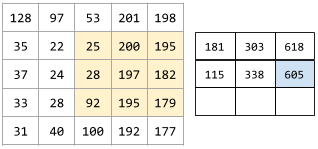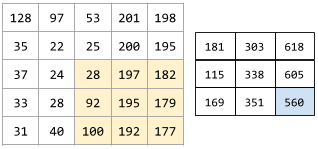
L'esempio precedente mostra un passo bidimensionale. Se la matrice di input è tridimensionale, anche il passo sarà tridimensionale.
sottocampionamento
Consulta la sezione pooling.
T
temperatura
Un iperparametro che controlla il grado di casualità dell'output di un modello. Temperature più alte comportano output più casuali, mentre temperature più basse generano output meno casuali.
La scelta della temperatura migliore dipende dall'applicazione specifica e dalle proprietà preferite dell'output del modello. Ad esempio, probabilmente alzi la temperatura quando crei un'applicazione che genera un output di creatività. Al contrario, probabilmente abbassiresti la temperatura quando crei un modello che classifica immagini o testo per migliorarne accuratezza e coerenza.
La temperatura viene spesso utilizzata con softmax.
invarianza di traduzione
In un problema di classificazione delle immagini, la capacità di un algoritmo di classificare correttamente le immagini anche quando la posizione degli oggetti all'interno dell'immagine cambia. Ad esempio, l'algoritmo è in grado di identificare comunque un cane, sia che si trovi al centro del frame o all'estremità sinistra del frame.
Vedi anche invarianza delle dimensioni e invarianza rotazionale.
