تحتوي هذه الصفحة على مصطلحات مسرد مصطلحات أساسيات تعلُّم الآلة. للاطّلاع على جميع مصطلحات المسرد، يُرجى النقر هنا.
A
الدقة
عدد التوقّعات الصحيحة للتصنيف مقسومًا على إجمالي عدد التوقّعات والمقصود:
على سبيل المثال، إذا قدّم نموذج 40 توقّعًا صحيحًا و10 توقّعات غير صحيحة، ستكون دقة النموذج كما يلي:
يقدّم التصنيف الثنائي أسماء محدّدة لمختلف فئات التوقعات الصحيحة والتوقعات غير الصحيحة. إذًا، صيغة الدقة للتصنيف الثنائي هي كما يلي:
where:
- TP هو عدد الحالات الموجبة الصحيحة (التوقّعات الصحيحة).
- TN هو عدد الحالات السالبة الصحيحة (التوقعات الصحيحة).
- FP هو عدد الحالات الموجبة الخاطئة (التوقعات غير الصحيحة).
- FN هو عدد الحالات السالبة الخاطئة (التوقعات غير الصحيحة).
تحديد أوجه التشابه والاختلاف بين الدقة والضبط والاسترجاع
يمكنك الاطّلاع على التصنيف: الدقة والاسترجاع والضبط والمقاييس ذات الصلة في "دورة تدريبية مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
دالّة التفعيل
هي دالة تتيح للشبكات العصبونية التعرّف على العلاقات غير الخطية (المعقّدة) بين الميزات والتصنيف.
تشمل دوال التنشيط الشائعة ما يلي:
لا تكون رسومات دوال التنشيط البيانية أبدًا خطوطًا مستقيمة مفردة. على سبيل المثال، يتألف رسم دالة التنشيط ReLU من خطين مستقيمين:

يبدو الرسم البياني لدالة التنشيط السينية كما يلي:

لمزيد من المعلومات، يُرجى الاطّلاع على الشبكات العصبية: دوال التنشيط في "الدورة التدريبية المكثّفة حول تعلُّم الآلة".
الذكاء الاصطناعي
برنامج أو نموذج غير بشري يمكنه حلّ المهام المعقّدة على سبيل المثال، يندرج ضمن الذكاء الاصطناعي برنامج أو نموذج يترجم النصوص، أو برنامج أو نموذج يحدّد الأمراض من صور الأشعة.
تعلُّم الآلة هو حقل فرعي من الذكاء الاصطناعي. مع ذلك، بدأت بعض المؤسسات في السنوات الأخيرة تستخدم مصطلحَي الذكاء الاصطناعي وتعلُّم الآلة بالتبادل.
المساحة تحت منحنى ROC
رقم يتراوح بين 0.0 و1.0 يمثّل قدرة نموذج التصنيف الثنائي على الفصل بين الفئات الإيجابية والفئات السلبية. كلما اقتربت قيمة AUC من 1.0، تحسّنت قدرة النموذج على فصل الفئات عن بعضها.
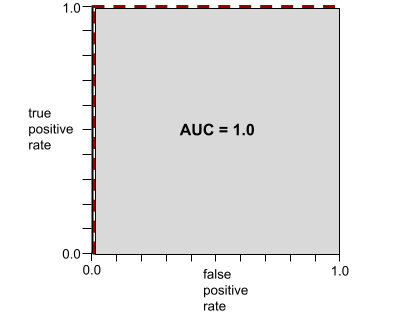
على سبيل المثال، توضّح الصورة التالية نموذج تصنيف يفصل تمامًا بين الفئات الإيجابية (الدوائر الخضراء) والفئات السلبية (المستطيلات الأرجوانية). يحتوي هذا النموذج المثالي بشكل غير واقعي على قيمة AUC تبلغ 1.0:

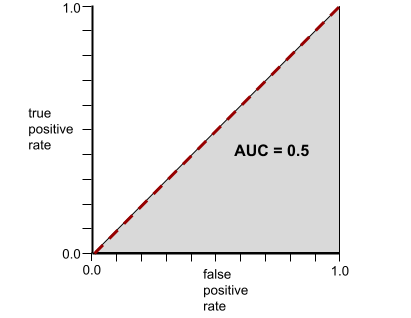
في المقابل، يوضّح الرسم التوضيحي التالي نتائج نموذج تصنيف أنشأ نتائج عشوائية. يحتوي هذا النموذج على قيمة AUC تبلغ 0.5:

نعم، النموذج السابق لديه قيمة AUC تبلغ 0.5، وليس 0.0.
وتقع معظم النماذج في مكان ما بين هذين الحدّين. على سبيل المثال، يفصل النموذج التالي بين القيم الإيجابية والسلبية إلى حد ما، وبالتالي يكون لديه قيمة AUC تتراوح بين 0.5 و1.0:

تتجاهل مقياس AUC أي قيمة تحدّدها لحدّ التصنيف. بدلاً من ذلك، تأخذ المساحة تحت منحنى ROC في الاعتبار جميع عتبات التصنيف الممكنة.
يمكنك الاطّلاع على التصنيف: منحنى ROC ومقياس AUC في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
B
الانتشار العكسي
الخوارزمية التي تنفّذ خوارزمية انحدار التدرّج في الشبكات العصبية
يتضمّن تدريب الشبكة العصبونية العديد من التكرارات للدورة التالية المكوّنة من مرحلتَين:
- أثناء التمرير الأمامي، يعالج النظام دفعة من الأمثلة لإنتاج التوقعات. يقارن النظام كل توقّع بقيمة كل تصنيف. الفرق بين القيمة المتوقّعة وقيمة التصنيف هو الخطأ في هذا المثال. يجمع النظام الخسائر لجميع الأمثلة من أجل احتساب إجمالي الخسارة للدُفعة الحالية.
- أثناء التمرير الخلفي (الانتشار الخلفي)، يقلّل النظام من الفقد من خلال تعديل أوزان جميع الخلايا العصبية في جميع الطبقات المخفية.
غالبًا ما تحتوي الشبكات العصبية على العديد من الخلايا العصبية في العديد من الطبقات المخفية. يساهم كل عصبون من هذه العصبونات في الخسارة الإجمالية بطرق مختلفة. تحدّد عملية الانتشار العكسي ما إذا كان يجب زيادة أو خفض الأوزان المطبَّقة على الخلايا العصبية المحدّدة.
معدّل التعلّم هو عامل ضرب يتحكّم في درجة زيادة أو خفض كل وزن في كل تمرير للخلف. سيؤدي معدّل التعلّم الكبير إلى زيادة أو خفض كل وزن بشكل أكبر من معدّل التعلّم الصغير.
من الناحية الحسابية، تنفّذ عملية الانتشار العكسي قاعدة السلسلة من الحساب التفاضلي. أي أنّ عملية الانتشار العكسي تحسب المشتق الجزئي للخطأ بالنسبة إلى كل مَعلمة.
قبل سنوات، كان على مطوّري تعلُّم الآلة كتابة تعليمات برمجية لتنفيذ الانتشار الخلفي. تنفّذ واجهات برمجة التطبيقات الحديثة لتعلُّم الآلة، مثل Keras، عملية الانتشار العكسي نيابةً عنك. أخيرًا!
يمكنك الاطّلاع على الشبكات العصبونية في "دورة مكثّفة عن تعلّم الآلة" لمزيد من المعلومات.
دفعة
مجموعة الأمثلة المستخدَمة في إحدى التكرارات التدريبية. يحدّد حجم الدفعة عدد الأمثلة في الدفعة.
راجِع الفترة للحصول على شرح حول كيفية ارتباط الدفعة بفترة.
يمكنك الاطّلاع على الانحدار الخطي: المَعلمات الفائقة في "دورة مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
حجم الدفعة
عدد الأمثلة في دفعة على سبيل المثال، إذا كان حجم الدفعة 100، سيعالج النموذج 100 مثال لكل تكرار.
في ما يلي استراتيجيات شائعة لحجم الدفعة:
- النزول المتدرّج العشوائي (SGD)، حيث يكون حجم الدفعة 1
- المجموعة الكاملة، حيث يكون حجم المجموعة هو عدد الأمثلة في مجموعة التدريب بأكملها. على سبيل المثال، إذا كانت مجموعة التدريب تحتوي على مليون مثال، سيكون حجم الدفعة مليون مثال. عادةً ما تكون الدفعة الكاملة استراتيجية غير فعّالة.
- الدُفعات الصغيرة التي يتراوح حجم الدفعة فيها عادةً بين 10 و1000. عادةً ما تكون استراتيجية الدُفعات الصغيرة هي الأكثر كفاءة.
يُرجى الاطّلاع على ما يلي لمزيد من المعلومات:
- أنظمة تعلُّم الآلة في مرحلة الإنتاج: الاستنتاج الثابت مقابل الاستنتاج الديناميكي في "دورة مكثّفة عن تعلُّم الآلة"
- Deep Learning Tuning Playbook
التحيّز (الأخلاقيات/العدالة)
1- الصور النمطية أو التحيز أو المحاباة تجاه بعض الأشياء أو الأشخاص أو المجموعات دون غيرها يمكن أن تؤثّر هذه الانحيازات في جمع البيانات وتفسيرها، وفي تصميم النظام، وفي طريقة تفاعل المستخدمين مع النظام. تشمل أشكال هذا النوع من التحيز ما يلي:
- تحيّز الأتمتة
- الانحياز التأكيدي
- تحيّز المجرب
- الانحياز لتشابه المجموعة
- التحيّز الضمني
- الانحياز لأفراد المجموعة
- الانحياز للتشابه خارج المجموعة
2. خطأ منهجي ناتج عن إجراءات أخذ العيّنات أو إعداد التقارير تشمل أشكال هذا النوع من التحيز ما يلي:
- انحياز في التغطية
- الانحياز لعدم الإجابة
- تحيّز المشاركة
- الانحياز لتكرار التقارير
- انحياز في جمع العيّنات
- الانحياز في الاختيار
يجب عدم الخلط بينها وبين مصطلح الانحياز في نماذج تعلُّم الآلة أو انحياز التوقّعات.
يمكنك الاطّلاع على الإنصاف: أنواع التحيز في "الدورة التدريبية المكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
الانحياز (في الرياضيات) أو مصطلح الانحياز
نقطة تقاطع أو إزاحة من نقطة الأصل التحيّز هو مَعلمة في نماذج تعلُّم الآلة، ويتم تمثيله بأحد الرمزين التاليين:
- b
- w0
على سبيل المثال، التحيز هو b في الصيغة التالية:
في خط بسيط ثنائي الأبعاد، يعني التحيز ببساطة "نقطة التقاطع مع المحور الصادي". على سبيل المثال، يكون ميل الخط في الرسم التوضيحي التالي هو 2.
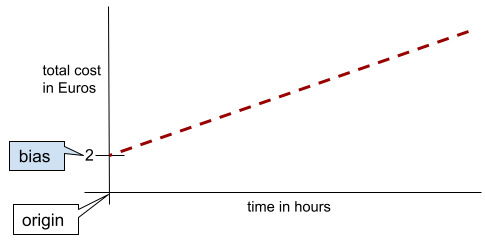
يحدث التحيز لأنّ بعض النماذج لا تبدأ من نقطة الأصل (0,0). على سبيل المثال، لنفترض أنّ تكلفة دخول مدينة ملاهٍ هي 2 يورو، بالإضافة إلى 0.5 يورو لكل ساعة يقضيها العميل فيها. وبالتالي، فإنّ النموذج الذي يربط التكلفة الإجمالية لديه تحيّز بمقدار 2 لأنّ أدنى تكلفة هي 2 يورو.
يجب عدم الخلط بين التحيز والتحيز في الأخلاق والعدالة أو التحيز في التوقعات.
يمكنك الاطّلاع على الانحدار الخطي في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
التصنيف الثنائي
نوع من مهام التصنيف التي تتوقّع إحدى الفئتين الحصريتين المتبادلتين:
على سبيل المثال، يؤدي نموذجا تعلُّم الآلة التاليان التصنيف الثنائي:
- نموذج يحدّد ما إذا كانت الرسائل الإلكترونية غير مرغوب فيها (الفئة الإيجابية) أو مرغوب فيها (الفئة السلبية).
- نموذج يقيّم الأعراض الطبية لتحديد ما إذا كان الشخص مصابًا بمرض معيّن (الفئة الإيجابية) أو غير مصاب به (الفئة السلبية).
يختلف عن التصنيف المتعدّد الفئات.
راجِع أيضًا الانحدار اللوجستي وحد التصنيف.
يمكنك الاطّلاع على التصنيف في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
تصنيف البيانات
تحويل سمة واحدة إلى سمات ثنائية متعددة تُعرف باسم حِزم أو فئات، عادةً ما يكون ذلك استنادًا إلى نطاق قيمة. عادةً ما تكون السمة المقطّعة سمة مستمرة.
على سبيل المثال، بدلاً من تمثيل درجة الحرارة كميزة واحدة مستمرة ذات فاصلة عائمة، يمكنك تقسيم نطاقات درجات الحرارة إلى فئات منفصلة، مثل:
- ستكون درجة الحرارة التي تقل عن أو تساوي 10 درجات مئوية ضمن الفئة "بارد".
- ستكون درجات الحرارة بين 11 و24 درجة مئوية ضمن الفئة "معتدلة".
- ستكون درجة الحرارة التي تبلغ 25 درجة مئوية أو أكثر ضمن الفئة "دافئ".
سيتعامل النموذج مع كل قيمة في المجموعة نفسها بشكل مماثل. على سبيل المثال، تندرج القيمتان 13 و22 ضمن الفئة المعتدلة، لذا يتعامل النموذج مع القيمتين بشكل مماثل.
لمزيد من المعلومات، راجِع البيانات الرقمية: التصنيف إلى فئات في "دورة مكثّفة عن تعلّم الآلة".
C
البيانات الفئوية
السمات التي تتضمّن مجموعة محدّدة من القيم المحتملة على سبيل المثال، لنفترض أنّ هناك ميزة فئوية باسم traffic-light-state، والتي يمكن أن تتضمّن إحدى القيم الثلاث التالية فقط:
redyellowgreen
من خلال تمثيل traffic-light-state كميزة فئوية، يمكن للنموذج التعرّف على التأثيرات المختلفة لكل من red وgreen وyellow في سلوك السائق.
يُطلق على الميزات الفئوية أحيانًا اسم الميزات المنفصلة.
يختلف عن البيانات الرقمية.
لمزيد من المعلومات، راجِع استخدام البيانات الفئوية في "الدورة التدريبية المكثّفة حول تعلُّم الآلة".
صنف
فئة يمكن أن ينتمي إليها تصنيف. على سبيل المثال:
- في نموذج التصنيف الثنائي الذي يرصد الرسائل غير المرغوب فيها، قد تكون الفئتان رسائل غير مرغوب فيها وليست رسائل غير مرغوب فيها.
- في نموذج التصنيف المتعدّد الفئات الذي يحدّد سلالات الكلاب، قد تكون الفئات بودل وبيغل وبَغ وما إلى ذلك.
يتنبأ نموذج التصنيف بفئة. في المقابل، يتنبأ نموذج الانحدار برقم بدلاً من فئة.
يمكنك الاطّلاع على التصنيف في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
نموذج التصنيف
نموذج يكون توقّعه فئة. على سبيل المثال، كلّ ما يلي هي نماذج تصنيف:
- نموذج يتوقّع لغة الجملة المُدخَلة (هل هي فرنسية؟ الإسبانية؟ الإيطالية؟
- نموذج يتوقّع أنواع الأشجار (قيقب؟ سنديان؟ Baobab?).
- نموذج يتوقّع الفئة الإيجابية أو السلبية لحالة طبية معيّنة.
في المقابل، تتنبّأ نماذج الانحدار بالأرقام بدلاً من الفئات.
في ما يلي نوعان شائعان من نماذج التصنيف:
عتبة التصنيف
في التصنيف الثنائي، يكون الناتج رقمًا بين 0 و1 يحوّل الناتج الأولي لنموذج الانحدار اللوجستي إلى توقع إما الفئة الإيجابية أو الفئة السلبية. يُرجى العِلم أنّ حدّ التصنيف هو قيمة يختارها الإنسان، وليس قيمة يختارها تدريب النموذج.
يُخرج نموذج الانحدار اللوجستي قيمة أولية بين 0 و1. بعد ذلك:
- إذا كانت هذه القيمة الأولية أكبر من حد التصنيف، سيتم توقّع الفئة الموجبة.
- إذا كانت هذه القيمة الأولية أقل من حد التصنيف، يتم التنبؤ بالفئة السلبية.
على سبيل المثال، لنفترض أنّ حد التصنيف هو 0.8. إذا كانت القيمة الأولية 0.9، يتوقّع النموذج الفئة الموجبة. إذا كانت القيمة الأولية 0.7، يتوقّع النموذج الفئة السلبية.
يؤثر اختيار حد التصنيف بشكل كبير في عدد الموجب الخاطئ و السالب الخاطئ.
يمكنك الاطّلاع على الحدود ومصفوفة الالتباس في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
مصنِّف
مصطلح غير رسمي يشير إلى نموذج التصنيف.
مجموعة بيانات غير متوازنة الفئات
مجموعة بيانات خاصة بالتصنيف يكون فيها العدد الإجمالي للتصنيفات الخاصة بكل فئة مختلفًا بشكل كبير. على سبيل المثال، لنفترض أنّ لديك مجموعة بيانات تصنيف ثنائي مقسّمة إلى فئتَين على النحو التالي:
- مليون تصنيف سلبي
- 10 تصنيفات إيجابية
نسبة التصنيفات السلبية إلى الإيجابية هي 100,000 إلى 1، لذا هذه مجموعة بيانات غير متوازنة الفئات.
في المقابل، مجموعة البيانات التالية متوازنة الفئات لأنّ نسبة التصنيفات السلبية إلى التصنيفات الإيجابية قريبة نسبيًا من 1:
- 517 تصنيفًا سلبيًا
- 483 تصنيفًا موجبًا
يمكن أن تكون مجموعات البيانات المتعددة الفئات غير متوازنة الفئات أيضًا. على سبيل المثال، مجموعة البيانات التالية الخاصة بالتصنيف المتعدد الفئات هي أيضًا غير متوازنة الفئات لأنّ إحدى التصنيفات تتضمّن أمثلة أكثر بكثير من التصنيفين الآخرين:
- 1,000,000 تصنيفًا مع الفئة "أخضر"
- 200 تصنيف من الفئة "أرجواني"
- 350 تصنيفًا من الفئة "برتقالي"
يمكن أن يواجه تدريب مجموعات البيانات غير المتوازنة الفئات تحديات خاصة. راجِع مجموعات البيانات غير المتوازنة في "دورة مكثّفة عن تعلّم الآلة" للحصول على التفاصيل.
راجِع أيضًا الإنتروبيا وفئة الأغلبية وفئة الأقلية.
القص
أسلوب للتعامل مع القيم الشاذة من خلال تنفيذ أحد الإجراءَين التاليَين أو كليهما:
- تخفيض قيم السمة التي تتجاوز الحد الأقصى إلى هذا الحد الأقصى
- زيادة قيم الميزات التي تقل عن الحد الأدنى إلى هذا الحد الأدنى
على سبيل المثال، لنفترض أنّ <0.5% من قيم ميزة معيّنة تقع خارج النطاق 40-60. في هذه الحالة، يمكنك إجراء ما يلي:
- يجب أن تكون جميع القيم التي تزيد عن 60 (الحدّ الأقصى) هي 60 بالضبط.
- يجب أن تكون جميع القيم الأقل من 40 (الحد الأدنى) هي 40 بالضبط.
يمكن أن تؤدي القيم الشاذة إلى إتلاف النماذج، ما يؤدي أحيانًا إلى تجاوز الأوزان للحد الأقصى أثناء التدريب. يمكن أن تؤدي بعض القيم الشاذة أيضًا إلى إفساد مقاييس مثل الدقة بشكل كبير. القص هو أسلوب شائع للحد من الضرر.
تفرض عملية اقتطاع التدرّج أن تكون قيم التدرّج ضمن نطاق محدّد أثناء التدريب.
يمكنك الاطّلاع على البيانات الرقمية: التسوية في "الدورة التدريبية المكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
مصفوفة نجاح التوقعات
جدول NxN يلخّص عدد التوقّعات الصحيحة والخاطئة التي قدّمها نموذج التصنيف. على سبيل المثال، إليك مصفوفة الالتباس التالية الخاصة بنموذج تصنيف ثنائي:
| ورم (متوقّع) | غير ورم (متوقّع) | |
|---|---|---|
| ورم (معلومات فعلية) | 18 (TP) | 1 (FN) |
| غير ورمي (معلومات فعلية) | 6 (FP) | 452 (TN) |
تعرض مصفوفة الالتباس السابقة ما يلي:
- من بين 19 توقّعًا كانت فيها الحقيقة الأساسية هي "ورم"، صنّف النموذج 18 منها بشكل صحيح وصنّف 1 منها بشكل غير صحيح.
- من بين 458 توقّعًا كانت الحقيقة الأساسية فيها هي "غير ورمي"، صنّف النموذج 452 منها بشكل صحيح و6 منها بشكل غير صحيح.
يمكن أن تساعدك مصفوفة الالتباس في تصنيف متعدد الفئات في تحديد أنماط الأخطاء. على سبيل المثال، لنفترض أنّ لديك مصفوفة الارتباك التالية لنموذج تصنيف متعدّد الفئات يتضمّن 3 فئات ويصنّف ثلاثة أنواع مختلفة من زهور السوسن (Virginica وVersicolor وSetosa). عندما كانت الحقيقة الأساسية هي Virginica، توضّح مصفوفة الخطأ أنّ النموذج كان أكثر عرضة للتنبؤ بأنّها Versicolor بدلاً من Setosa:
| Setosa (متوقّع) | Versicolor (القيمة المتوقّعة) | Virginica (القيمة المتوقّعة) | |
|---|---|---|---|
| Setosa (المعلومات الفعلية) | 88 | 12 | 0 |
| Versicolor (المعلومات الفعلية) | 6 | 141 | 7 |
| Virginica (المعلومات الفعلية) | 2 | 27 | 109 |
كمثال آخر، يمكن أن تكشف مصفوفة الالتباس أنّ نموذجًا تم تدريبه على التعرّف على الأرقام المكتوبة بخط اليد يميل إلى توقّع الرقم 9 بدلاً من 4، أو توقّع الرقم 1 بدلاً من 7.
تحتوي مصفوفات الالتباس على معلومات كافية لحساب مجموعة متنوعة من مقاييس الأداء، بما في ذلك الدقة والاستدعاء.
خاصية مستمرة
ميزة ذات فاصلة عشرية عائمة مع نطاق لا نهائي من القيم المحتملة، مثل درجة الحرارة أو الوزن
يجب التمييز بينها وبين الخاصية المحدّدة القيم.
التقارب
هي حالة يتم الوصول إليها عندما تتغير قيم الخسارة بشكل طفيف جدًا أو لا تتغير على الإطلاق مع كل تكرار. على سبيل المثال، يشير منحنى الخسارة التالي إلى التقارب عند حوالي 700 تكرار:
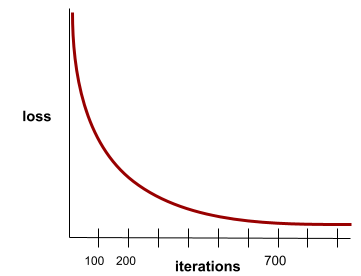
يتقارب النموذج عندما لا يؤدي التدريب الإضافي إلى تحسينه.
في التعلم العميق، تظل قيم الخسارة ثابتة أحيانًا أو قريبة من ذلك لعدة تكرارات قبل أن تنخفض أخيرًا. خلال فترة طويلة من القيم الثابتة للخسارة، قد تشعر مؤقتًا بشكل خاطئ بالتقارب.
اطّلِع أيضًا على الإيقاف المبكر.
لمزيد من المعلومات، يُرجى الاطّلاع على تقارب النماذج ومنحنيات الخسارة في "دورة تدريبية مكثّفة حول تعلُّم الآلة".
D
DataFrame
نوع بيانات pandas شائع لتمثيل مجموعات البيانات في الذاكرة
يشبه DataFrame الجدول أو جدول البيانات. يحتوي كل عمود في DataFrame على اسم (عنوان)، ويتم تحديد كل صف برقم فريد.
يتم تنظيم كل عمود في إطار البيانات على شكل مصفوفة ثنائية الأبعاد، إلا أنّه يمكن تعيين نوع بيانات خاص لكل عمود.
يمكنك أيضًا الاطّلاع على صفحة pandas.DataFrame المرجعية الرسمية.
مجموعة البيانات
مجموعة من البيانات الأولية، يتم تنظيمها عادةً (وليس حصريًا) بأحد التنسيقات التالية:
- جدول بيانات
- ملف بتنسيق CSV (قيم مفصولة بفواصل)
نموذج عميق
شبكة عصبية تحتوي على أكثر من طبقة مخفية
يُطلق على النموذج العميق أيضًا اسم شبكة عصبية عميقة.
يختلف عن النموذج الواسع.
خاصية كثيفة
ميزة تكون معظم قيمها أو كلها غير صفرية، وعادةً ما تكون Tensor من قيم الفاصلة العائمة. على سبيل المثال، يكون Tensor التالي المكوّن من 10 عناصر كثيفًا لأنّ 9 من قيمه غير صفرية:
| 8 | 3 | 7 | 5 | 2 | 4 | 0 | 4 | 9 | 6 |
يختلف عن الميزة النادرة.
العمق
مجموع ما يلي في شبكة عصبونية:
- عدد الطبقات المخفية
- عدد الطبقات النهائية، وهو عادةً 1
- عدد أي طبقات تضمين
على سبيل المثال، تبلغ عمق الشبكة العصبية التي تتضمّن خمس طبقات مخفية وطبقة إخراج واحدة 6 طبقات.
يُرجى العِلم أنّ طبقة الإدخال لا تؤثر في العمق.
خاصية محدّدة القيم
الميزة التي تتضمّن مجموعة محدودة من القيم المحتملة على سبيل المثال، السمة التي لا يمكن أن تتضمّن قيمًا سوى حيوان أو نبات أو معدن هي سمة منفصلة (أو فئوية).
يختلف عن الخاصية المستمرة.
ديناميكي
شيء يتم إجراؤه بشكل متكرّر أو مستمر المصطلحان ديناميكي وعلى الإنترنت مترادفان في تعلُّم الآلة. في ما يلي الاستخدامات الشائعة للديناميكية والإنترنت في تعلّم الآلة:
- النموذج الديناميكي (أو النموذج المباشر) هو نموذج تتم إعادة تدريبه بشكل متكرر أو مستمر.
- التدريب الديناميكي (أو التدريب على الإنترنت) هو عملية تدريب متكررة أو مستمرة.
- الاستدلال الديناميكي (أو الاستدلال المباشر) هو عملية إنشاء توقعات عند الطلب.
نموذج ديناميكي
نموذج يتم إعادة تدريبه بشكل متكرر (ربما بشكل مستمر). النموذج الديناميكي هو "متعلّم مدى الحياة" يتكيّف باستمرار مع البيانات المتطورة. يُعرف النموذج الديناميكي أيضًا باسم النموذج المباشر.
يختلف عن النموذج الثابت.
E
الإيقاف المبكر
إحدى طرق التسوية التي تتضمّن إنهاء التدريب قبل أن يتوقف معدّل انخفاض خسارة التدريب. في عملية الإيقاف المبكر، يتم إيقاف تدريب النموذج عمدًا عندما يبدأ معدل الخطأ في مجموعة بيانات التحقّق من الصحة في الارتفاع، أي عندما يتدهور أداء التعميم.
يختلف ذلك عن الخروج المبكر.
طبقة التضمين
طبقة مخفية خاصة يتم تدريبها على سمة فئوية ذات أبعاد عالية من أجل التعلّم تدريجيًا لمتجه تضمين ذي أبعاد أقل. تتيح طبقة التضمين للشبكة العصبونية التدريب بكفاءة أكبر بكثير من التدريب على الميزة الفئوية العالية الأبعاد فقط.
على سبيل المثال، يتيح Earth حاليًا حوالي 73,000 نوع من الأشجار. لنفترض أنّ نوع الشجرة هو سمة في نموذجك، وبالتالي تتضمّن طبقة الإدخال في نموذجك متجهًا ذا ترميز ساخن بطول 73,000 عنصر.
على سبيل المثال، قد يتم تمثيل baobab على النحو التالي:

إنّ مصفوفة تضم 73,000 عنصر طويلة جدًا. إذا لم تُضِف طبقة تضمين إلى النموذج، سيستغرق التدريب وقتًا طويلاً جدًا بسبب ضرب 72,999 صفرًا. لنفترض أنّك اخترت أن تتكوّن طبقة التضمين من 12 سمة. وبالتالي، ستتعلّم طبقة التضمين تدريجيًا متجه تضمين جديدًا لكل نوع من أنواع الأشجار.
في حالات معيّنة، يكون التجزئة بديلاً معقولاً لطبقة التضمين.
يمكنك الاطّلاع على التضمينات في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
حقبة
هي عملية تدريب كاملة على مجموعة التدريب بحيث تتم معالجة كل مثال مرة واحدة.
يمثّل العصر N/حجم الدفعة
تكرارات التدريب، حيث يمثّل N
إجمالي عدد الأمثلة.
على سبيل المثال، لنفترض ما يلي:
- تتألف مجموعة البيانات من 1,000 مثال.
- يبلغ حجم الدفعة 50 مثالاً.
لذلك، تتطلّب الحقبة الواحدة 20 تكرارًا:
1 epoch = (N/batch size) = (1,000 / 50) = 20 iterations
يمكنك الاطّلاع على الانحدار الخطي: المَعلمات الفائقة في "دورة مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
على سبيل المثال
قيم أحد صفوف الميزات وربما تصنيف تندرج الأمثلة في التعلم المُوجّه ضمن فئتين عامّتَين:
- يتألف المثال المصنّف من ميزة واحدة أو أكثر وتصنيف. يتم استخدام الأمثلة المصنَّفة أثناء التدريب.
- يتألف مثال غير مصنّف من ميزة واحدة أو أكثر بدون تصنيف. يتم استخدام الأمثلة غير المصنّفة أثناء الاستدلال.
على سبيل المثال، لنفترض أنّك تدرب نموذجًا لتحديد تأثير الظروف الجوية على درجات اختبار الطلاب. في ما يلي ثلاثة أمثلة مصنّفة:
| الميزات | التصنيف | ||
|---|---|---|---|
| درجة الحرارة | الرطوبة | الضغط | نتيجة الاختبار |
| 15 | 47 | 998 | جيدة |
| 19 | 34 | 1020 | ممتاز |
| 18 | 92 | 1012 | سيئة |
في ما يلي ثلاثة أمثلة غير مصنّفة:
| درجة الحرارة | الرطوبة | الضغط | |
|---|---|---|---|
| 12 | 62 | 1014 | |
| 21 | 47 | 1017 | |
| 19 | 41 | 1021 |
عادةً ما يكون صف مجموعة البيانات هو المصدر الأولي للمثال. أي أنّ المثال يتألف عادةً من مجموعة فرعية من الأعمدة في مجموعة البيانات. بالإضافة إلى ذلك، يمكن أن تتضمّن الميزات في أحد الأمثلة أيضًا ميزات اصطناعية، مثل تقاطع الميزات.
يمكنك الاطّلاع على التعلم الخاضع للإشراف في دورة "مقدمة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
F
سالب خاطئ (FN)
مثال يخطئ فيه النموذج في التنبؤ بالفئة السلبية. على سبيل المثال، يتوقّع النموذج أنّ رسالة إلكترونية معيّنة ليست رسالة غير مرغوب فيها (الفئة السلبية)، ولكنّ هذه الرسالة الإلكترونية هي في الواقع رسالة غير مرغوب فيها.
موجب خاطئ
مثال يخطئ فيه النموذج في التنبؤ بالفئة الإيجابية. على سبيل المثال، يتوقّع النموذج أنّ رسالة إلكترونية معيّنة هي رسالة غير مرغوب فيها (الفئة الإيجابية)، ولكن في الواقع، هذه الرسالة ليست رسالة غير مرغوب فيها.
يمكنك الاطّلاع على الحدود ومصفوفة الالتباس في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
معدّل الموجب الخاطئ
يشير ذلك المصطلح إلى نسبة الأمثلة السلبية الفعلية التي توقّع النموذج بشكل خاطئ أنّها تنتمي إلى الفئة الإيجابية. تحتسب الصيغة التالية معدّل الإيجابية الخاطئة:
معدل الموجب الخاطئ هو المحور السيني في منحنى خاصية تشغيل جهاز الاستقبال.
يمكنك الاطّلاع على التصنيف: منحنى ROC ومقياس AUC في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
ميزة
متغيّر إدخال في نموذج تعلُّم الآلة يتألف المثال من ميزة واحدة أو أكثر. على سبيل المثال، لنفترض أنّك تدرب نموذجًا لتحديد تأثير الظروف الجوية على درجات الطلاب في الاختبارات. يعرض الجدول التالي ثلاثة أمثلة، يحتوي كل منها على ثلاث سمات وتصنيف واحد:
| الميزات | التصنيف | ||
|---|---|---|---|
| درجة الحرارة | الرطوبة | الضغط | نتيجة الاختبار |
| 15 | 47 | 998 | 92 |
| 19 | 34 | 1020 | 84 |
| 18 | 92 | 1012 | 87 |
التباين مع التصنيف
يمكنك الاطّلاع على التعلّم بإشراف في دورة "مقدمة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
مضروب مجموعات الخصائص
الخاصية الاصطناعية هي خاصية تم إنشاؤها من خلال "دمج" الخصائص الفئوية أو الخصائص المقسَّمة إلى مجموعات.
على سبيل المثال، لنفترض أنّ لديك نموذجًا "لتوقّع الحالة المزاجية" يمثّل درجة الحرارة في إحدى الفئات الأربع التالية:
freezingchillytemperatewarm
وتمثّل سرعة الرياح في إحدى الفئات الثلاث التالية:
stilllightwindy
بدون عمليات الربط بين الميزات، يتم تدريب النموذج الخطي بشكل مستقل على كل من المجموعات السبع المختلفة السابقة. لذا، يتدرب النموذج على، على سبيل المثال،
freezing بشكل مستقل عن التدريب على، على سبيل المثال،
windy.
يمكنك بدلاً من ذلك إنشاء تقاطع ميزات لدرجة الحرارة وسرعة الرياح. ستتضمّن هذه السمة الاصطناعية 12 قيمة محتملة على النحو التالي:
freezing-stillfreezing-lightfreezing-windychilly-stillchilly-lightchilly-windytemperate-stilltemperate-lighttemperate-windywarm-stillwarm-lightwarm-windy
بفضل عمليات الربط بين الميزات، يمكن للنموذج التعرّف على الاختلافات في الحالة المزاجية بين يوم freezing-windy ويوم freezing-still.
إذا أنشأت ميزة اصطناعية من ميزتَين تحتوي كل منهما على الكثير من التصنيفات المختلفة، سيحتوي تقاطع الميزتَين الناتج على عدد كبير من المجموعات المحتملة. على سبيل المثال، إذا كانت إحدى الميزات تتضمّن 1,000 مجموعة والأخرى تتضمّن 2,000 مجموعة، ستحتوي الميزة الناتجة على 2,000,000 مجموعة.
رياضيًا، يكون التقاطع ناتجًا ديكارتيًا.
يتم استخدام عمليات ضرب الميزات بشكل أساسي مع النماذج الخطية، ونادرًا ما يتم استخدامها مع الشبكات العصبية.
يمكنك الاطّلاع على البيانات الفئوية: التقاطعات بين الميزات في "دورة مكثّفة عن تعلُّم الآلة" للحصول على مزيد من المعلومات.
هندسة الميزات
عملية تتضمّن الخطوات التالية:
- تحديد الميزات التي قد تكون مفيدة في تدريب نموذج
- تحويل البيانات الأولية من مجموعة البيانات إلى إصدارات فعّالة من هذه الميزات
على سبيل المثال، قد ترى أنّ temperature قد تكون ميزة مفيدة. بعد ذلك، يمكنك تجربة التجميع في فئات
لتحسين ما يمكن أن يتعلّمه النموذج من نطاقات temperature المختلفة.
يُطلق على عملية تصميم الميزات أحيانًا اسم استخراج الميزات أو تحويل البيانات إلى ميزات.
راجِع البيانات الرقمية: كيف يستوعب النموذج البيانات باستخدام متجهات الميزات في "دورة تدريبية مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
مجموعة الميزات
مجموعة الميزات التي يتم تدريب نموذج تعلُّم الآلة عليها على سبيل المثال، قد تتألف مجموعة بسيطة من السمات لنموذج يتنبأ بأسعار المساكن من الرمز البريدي ومساحة العقار وحالته.
متّجه الميزات
مصفوفة قيم الميزة التي تتضمّن مثالاً. يتم إدخال متجه الميزات أثناء التدريب وأثناء الاستدلال. على سبيل المثال، قد يكون متجه الميزات لنموذج يتضمّن ميزتَين منفصلتَين كما يلي:
[0.92, 0.56]

يقدّم كل مثال قيمًا مختلفة لمتّجه الميزات، لذا يمكن أن يكون متّجه الميزات للمثال التالي على النحو التالي:
[0.73, 0.49]
تحدّد هندسة الميزات كيفية تمثيل الميزات في متجه الميزات. على سبيل المثال، يمكن تمثيل ميزة فئوية ثنائية ذات خمس قيم محتملة باستخدام الترميز الساخن. في هذه الحالة، سيتألف جزء متجه الميزات الخاص بمثال معيّن من أربعة أصفار و1.0 واحد في الموضع الثالث، كما يلي:
[0.0, 0.0, 1.0, 0.0, 0.0]
كمثال آخر، لنفترض أنّ نموذجك يتكوّن من ثلاث ميزات:
- سمة فئوية ثنائية ذات خمس قيم محتملة يتم تمثيلها باستخدام الترميز الساخن، على سبيل المثال:
[0.0, 1.0, 0.0, 0.0, 0.0] - سمة فئوية ثنائية أخرى تتضمّن ثلاث قيم محتملة ممثّلة باستخدام الترميز الأحادي، مثل:
[0.0, 0.0, 1.0] - سمة نقطة عائمة، على سبيل المثال:
8.3
في هذه الحالة، سيتم تمثيل متجه الميزات لكل مثال بتسع قيم. بالنظر إلى القيم النموذجية في القائمة السابقة، سيكون متجه الميزات كما يلي:
0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 8.3
راجِع البيانات الرقمية: كيف يستوعب النموذج البيانات باستخدام متجهات الميزات في "دورة تدريبية مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
حلقة الملاحظات
في تعلُّم الآلة، هي حالة تؤثّر فيها توقّعات النموذج في بيانات التدريب الخاصة بالنموذج نفسه أو نموذج آخر. على سبيل المثال، سيؤثر نموذج يقترح أفلامًا في الأفلام التي يشاهدها المستخدمون، ما سيؤثر بدوره في نماذج اقتراح الأفلام اللاحقة.
لمزيد من المعلومات، يمكنك الاطّلاع على أنظمة تعلُّم الآلة الجاهزة للاستخدام: أسئلة يجب طرحها في "الدورة التدريبية المكثّفة حول تعلُّم الآلة".
G
التعميم
تشير إلى قدرة النموذج على تقديم توقّعات صحيحة بشأن بيانات جديدة لم يسبق له رؤيتها. النموذج الذي يمكنه التعميم هو عكس النموذج الذي يفرط في التوافق.
يمكنك الاطّلاع على التعميم في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
منحنى التعميم
رسم بياني لكل من فقدان التدريب وفقدان التحقّق كدالة لعدد التكرارات
يمكن أن يساعدك منحنى التعميم في رصد حالات التطابق الزائد المحتملة. على سبيل المثال، يشير منحنى التعميم التالي إلى زيادة الملاءمة لأنّ خسارة التحقّق تصبح في النهاية أعلى بكثير من خسارة التدريب.
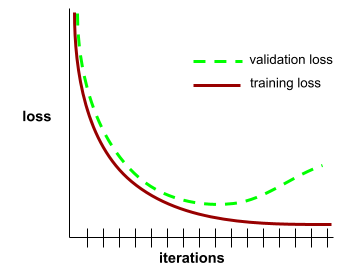
يمكنك الاطّلاع على التعميم في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
النزول المتدرّج
أسلوب رياضي للحدّ من الخسارة. تعمل عملية "انحدار التدرّج" على تعديل الأوزان والانحيازات بشكل متكرّر، وتعثر تدريجيًا على أفضل تركيبة لتقليل الخسارة.
تسبق طريقة "انحدار التدرّج" تقنية تعلُّم الآلة بفترة طويلة جدًا.
يمكنك الاطّلاع على الانحدار الخطي: نزول التدرّج في "الدورة التدريبية المكثّفة حول تعلُّم الآلة" لمزيد من المعلومات.
معلومات فعلية
الواقع
الشيء الذي حدث بالفعل
على سبيل المثال، لنفترض أنّ هناك نموذج تصنيف ثنائي يتوقّع ما إذا كان الطالب في سنته الأولى بالجامعة سيتخرّج في غضون ست سنوات. تتمثل الحقيقة الأساسية لهذا النموذج في ما إذا كان الطالب قد تخرّج بالفعل في غضون ست سنوات أم لا.
H
الطبقة المخفية
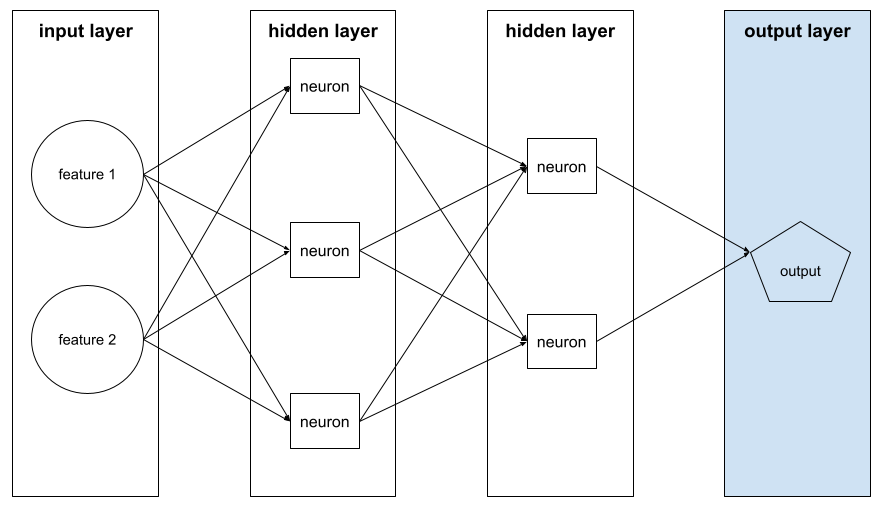
هي طبقة في شبكة عصبية بين طبقة الإدخال (الميزات) وطبقة الإخراج (التوقّع). تتكوّن كل طبقة مخفية من خلية عصبية واحدة أو أكثر. على سبيل المثال، تحتوي الشبكة العصبية التالية على طبقتَين مخفيتَين، الأولى تحتوي على ثلاث خلايا عصبية والثانية على خليتَين عصبيتين:
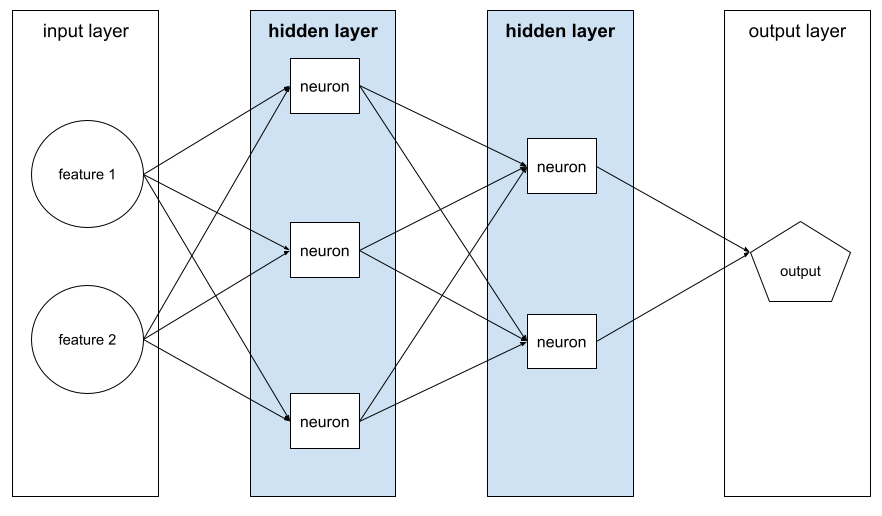
تحتوي الشبكة العصبية العميقة على أكثر من طبقة مخفية واحدة. على سبيل المثال، الرسم التوضيحي السابق هو شبكة عصبية عميقة لأنّ النموذج يحتوي على طبقتَين مخفيتَين.
يمكنك الاطّلاع على الشبكات العصبية: العُقد والطبقات المخفية في "دورة تدريبية مكثّفة حول تعلُّم الآلة" لمزيد من المعلومات.
مَعلمة فائقة
المتغيرات التي يتم تعديلها أثناء عمليات التدريب المتتالية للنموذج، سواء تم ذلك من خلالك أو من خلال خدمة ضبط المعلمات الفائقة على سبيل المثال، معدّل التعلّم هو معلَمة فائقة. يمكنك ضبط معدّل التعلّم على 0.01 قبل جلسة تدريب واحدة. إذا تبيّن لك أنّ القيمة 0.01 مرتفعة جدًا، يمكنك ضبط معدّل التعلّم على 0.003 لجلسة التدريب التالية.
في المقابل، المَعلمات هي الأوزان والانحيازات المختلفة التي يتعلّمها النموذج أثناء التدريب.
يمكنك الاطّلاع على الانحدار الخطي: المَعلمات الفائقة في "دورة مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
I
موزّعة بشكل مستقل ومتشابه
البيانات المستخلصة من توزيع لا يتغيّر، ولا تعتمد فيه كل قيمة مستخلصة على القيم التي تم استخلاصها سابقًا. إنّ التوزيع المتطابق والمستقل هو الغاز المثالي في مجال تعلُّم الآلة، وهو بنية رياضية مفيدة ولكنّها نادرًا ما توجد بالضبط في العالم الحقيقي. على سبيل المثال، قد يكون توزيع الزوّار على صفحة ويب متطابقًا ومستقلاً على مدار فترة زمنية قصيرة، أي أنّ التوزيع لا يتغيّر خلال تلك الفترة القصيرة، وتكون زيارة أحد الأشخاص مستقلة بشكل عام عن زيارة شخص آخر. ومع ذلك، إذا وسّعت نطاق هذا الإطار الزمني، قد تظهر اختلافات موسمية في عدد زوّار صفحة الويب.
يمكنك الاطّلاع أيضًا على عدم الثبات.
الاستنتاج
في عملية تعلُّم الآلة التقليدية، يتم إجراء التوقعات من خلال تطبيق نموذج مدرَّب على أمثلة غير مصنَّفة. يمكنك الاطّلاع على التعلم الخاضع للإشراف في دورة "مقدمة في تعلُّم الآلة" لمعرفة المزيد.
في النماذج اللغوية الكبيرة، الاستدلال هو عملية استخدام نموذج مُدرَّب لإنشاء رد على طلب.
للاستدلال معنى مختلف إلى حد ما في الإحصاء. يمكنك الاطّلاع على مقالة الاستدلال الإحصائي على ويكيبيديا للحصول على التفاصيل.
طبقة الإدخال
الطبقة في الشبكة العصبونية التي تحتوي على متجه الميزات أي أنّ طبقة الإدخال توفّر أمثلة من أجل التدريب أو الاستنتاج. على سبيل المثال، تتألف طبقة الإدخال في الشبكة العصبية التالية من ميزتَين:
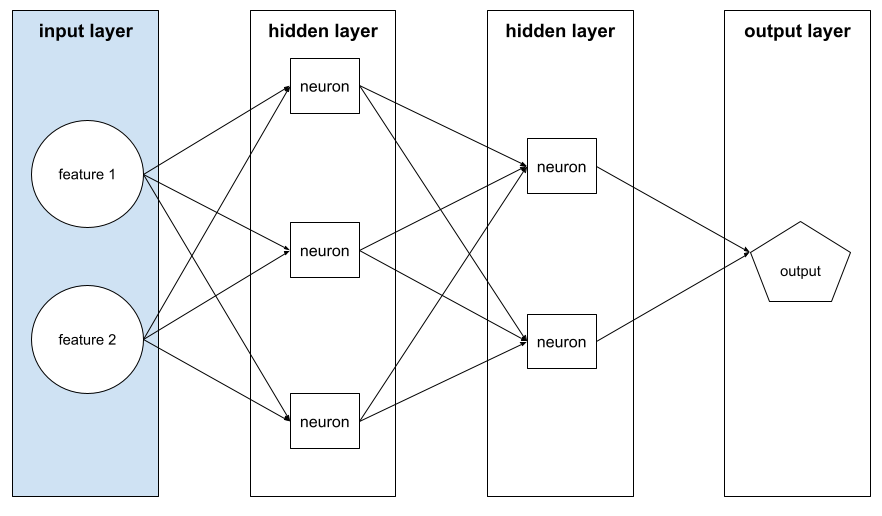
القابلية للتفسير
تشير إلى القدرة على شرح أو عرض طريقة تفكير نموذج تعلُّم الآلة بعبارات يسهل على الإنسان فهمها.
معظم نماذج الانحدار الخطي، على سبيل المثال، يمكن تفسيرها بشكل كبير. (ما عليك سوى الاطّلاع على القيم التقديرية التي تم تدريبها لكل ميزة). تتسم غابات القرارات أيضًا بقابلية تأويل عالية. ومع ذلك، تتطلّب بعض النماذج عرضًا مرئيًا متطوّرًا لتصبح قابلة للتفسير.
يمكنك استخدام أداة Learning Interpretability Tool (LIT) لتفسير نماذج تعلُّم الآلة.
التكرار
تعديل واحد على مَعلمات النموذج، أي الأوزان والانحيازات، أثناء التدريب. يحدّد حجم الدفعة عدد الأمثلة التي يعالجها النموذج في تكرار واحد. على سبيل المثال، إذا كان حجم الدفعة 20، سيعالج النموذج 20 مثالاً قبل تعديل المَعلمات.
عند تدريب شبكة عصبونية، تتضمّن عملية التكرار الواحدة الخطوتَين التاليتَين:
- تمريرة للأمام لتقييم الخسارة في دفعة واحدة
- عملية تمرير عكسي (الانتشار العكسي) لضبط معلَمات النموذج استنادًا إلى الخسارة ومعدّل التعلّم
لمزيد من المعلومات، يمكنك الاطّلاع على النزول التدريجي في "دورة مكثّفة عن تعلّم الآلة".
L
التسوية 0
أحد أنواع التسوية التي تعاقب العدد الإجمالي للأوزان غير الصفرية في أحد النماذج. على سبيل المثال، سيتم فرض عقوبة أكبر على نموذج يتضمّن 11 وزنًا غير صفري مقارنةً بنموذج مشابه يتضمّن 10 أوزان غير صفرية.
يُطلق على تسوية L0 أحيانًا اسم تسوية L0-norm.
خسارة L1
دالة الخسارة التي تحسب القيمة المطلقة للفرق بين قيم التصنيف الفعلية والقيم التي يتوقّعها النموذج. على سبيل المثال، إليك طريقة حساب خسارة L1 لمجموعة من خمسة أمثلة:
| القيمة الفعلية للمثال | القيمة المتوقّعة للنموذج | القيمة المطلقة للتغيير |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 3 |
| 4 | 6 | 2 |
| 9 | 8 | 1 |
| 8 = خسارة L1 | ||
يكون مقياس L1 أقل حساسية للقيم الشاذة من مقياس L2.
متوسط الخطأ المطلق هو متوسط خسارة 1 لكل مثال.
يمكنك الاطّلاع على الانحدار الخطي: الخسارة في "الدورة التدريبية المكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
التسوية من النوع L1
نوع من التسوية يفرض عقوبة على الأوزان بما يتناسب مع مجموع القيمة المطلقة للأوزان. يساعد التسوية من النوع L1 في ضبط أوزان الميزات غير الملائمة أو غير المهمة على 0 تمامًا. تتم إزالة ميزة ذات وزن 0 من النموذج بشكل فعّال.
يجب عدم الخلط بينها وبين التسوية من النوع L2.
خسارة 2
يشير ذلك المصطلح إلى دالة خسارة تحسب مربع الفرق بين قيم التصنيف الفعلية والقيم التي يتوقّعها النموذج. على سبيل المثال، إليك طريقة حساب خسارة L2 لمجموعة من خمسة أمثلة:
| القيمة الفعلية للمثال | القيمة المتوقّعة للنموذج | مربع دلتا |
|---|---|---|
| 7 | 6 | 1 |
| 5 | 4 | 1 |
| 8 | 11 | 9 |
| 4 | 6 | 4 |
| 9 | 8 | 1 |
| 16 = L2 خسارة | ||
بسبب التربيع، يؤدي فقدان L2 إلى تضخيم تأثير القيم الشاذة. أي أنّ دالة الخسارة L2 تتأثر بشكل أكبر بالتوقعات السيئة مقارنةً بدالة الخسارة L1. على سبيل المثال، سيكون معدّل فقدان حزمة L1 السابقة 8 بدلاً من 16. لاحظ أنّ قيمة متطرفة واحدة تمثّل 9 من أصل 16.
تستخدم نماذج الانحدار عادةً دالة الخسارة L2 كدالة خسارة.
متوسط الخطأ التربيعي هو متوسط خسارة 2 لكل مثال. الخسارة التربيعية هي اسم آخر للخسارة من النوع L2.
يمكنك الاطّلاع على الانحدار اللوجستي: الخسارة والتسوية في "الدورة التدريبية المكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
التسوية 2
أحد أنواع التسوية التي تعاقب الأوزان بما يتناسب مع مجموع مربعات الأوزان. تساعد عملية التسوية L2 في تقريب أوزان القيم الشاذة (التي تتضمّن قيمًا موجبة عالية أو قيمًا سالبة منخفضة) إلى 0، ولكن ليس تمامًا إلى 0. تبقى الميزات التي تتضمّن قيمًا قريبة جدًا من 0 في النموذج، ولكنّها لا تؤثّر كثيرًا في التوقّعات التي يقدّمها النموذج.
يؤدي التسوية L2 دائمًا إلى تحسين التعميم في النماذج الخطية.
يختلف عن التسوية من النوع L1.
لمزيد من المعلومات، يمكنك الاطّلاع على الإفراط في التخصيص: التسوية L2 في "دورة مكثّفة حول تعلُّم الآلة".
التصنيف
في تعلُّم الآلة الموجَّه، يمثّل هذا المصطلح جزء "الإجابة" أو "النتيجة" في مثال.
يتألف كل مثال مصنّف من ميزات واحدة أو أكثر وتصنيف. على سبيل المثال، في مجموعة بيانات مخصّصة لرصد المحتوى غير المرغوب فيه، من المحتمل أن يكون التصنيف إما "محتوى غير مرغوب فيه" أو "ليس محتوًى غير مرغوب فيه". في مجموعة بيانات خاصة بهطول الأمطار، قد يكون التصنيف هو كمية الأمطار التي هطلت خلال فترة زمنية معيّنة.
يمكنك الاطّلاع على التعلم الخاضع للإشراف في "مقدمة عن تعلُّم الآلة" للحصول على مزيد من المعلومات.
مثال مصنّف
مثال يتضمّن ميزات واحدة أو أكثر وتصنيفًا على سبيل المثال، يعرض الجدول التالي ثلاثة أمثلة مصنّفة من نموذج لتقييم المنازل، ويتضمّن كل مثال ثلاث سمات وتصنيفًا واحدًا:
| عدد غرف النوم | عدد الحمّامات | عمر المنزل | سعر المنزل (التصنيف) |
|---|---|---|---|
| 3 | 2 | 15 | 345,000 دولار أمريكي |
| 2 | 1 | 72 | 179,000 دولار أمريكي |
| 4 | 2 | 34 | $392,000 |
في تعلُّم الآلة الموجَّه، يتم تدريب النماذج على أمثلة مصنَّفة، ويتم إجراء توقعات على أمثلة غير مصنَّفة.
قارِن بين الأمثلة المصنّفة والأمثلة غير المصنّفة.
يمكنك الاطّلاع على التعلم الخاضع للإشراف في "مقدمة عن تعلُّم الآلة" للحصول على مزيد من المعلومات.
lambda
مرادف معدل التسوية
Lambda هو مصطلح متعدد المعاني. نركّز هنا على تعريف المصطلح ضمن التسوية.
طبقة
مجموعة من الخلايا العصبية في شبكة عصبية في ما يلي ثلاثة أنواع شائعة من الطبقات:
- طبقة الإدخال، التي توفّر قيمًا لجميع المعالم
- طبقة مخفية واحدة أو أكثر، والتي تعثر على علاقات غير خطية بين السمات والتصنيف
- طبقة الإخراج، التي تقدّم التوقّع
على سبيل المثال، يوضّح الرسم التوضيحي التالي شبكة عصبية تتضمّن طبقة إدخال واحدة وطبقتَين مخفيتَين وطبقة إخراج واحدة:
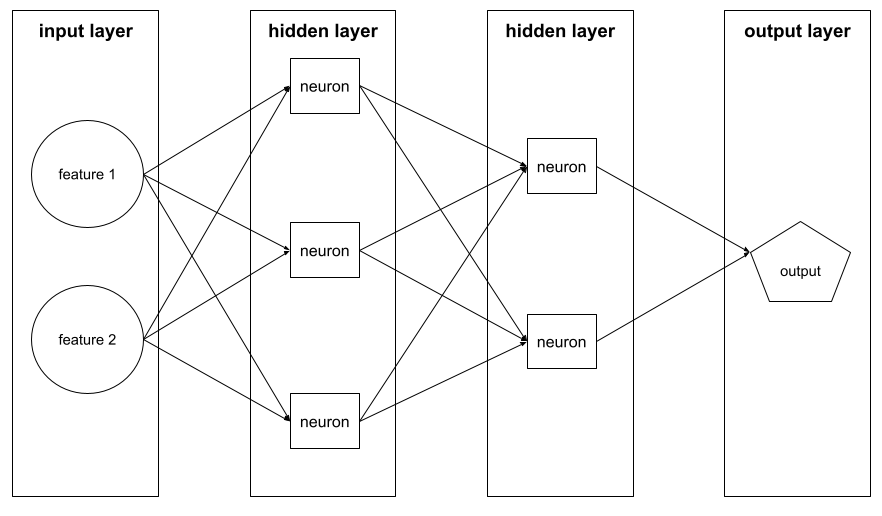
في TensorFlow، تكون الطبقات أيضًا عبارة عن دوال Python تأخذ موترات وخيارات إعداد كمدخلات وتنتج موترات أخرى كمخرجات.
معدّل التعلّم
عدد ذو فاصلة عائمة يحدّد للخوارزمية النزول بالتدرّج مدى قوة تعديل الأوزان والانحيازات في كل تكرار. على سبيل المثال، يؤدي معدّل التعلّم البالغ 0.3 إلى تعديل الأوزان والانحيازات بقوة أكبر بثلاث مرات من معدّل التعلّم البالغ 0.1.
معدّل التعلّم هو مَعلمة فائقة أساسية. إذا ضبطت معدّل التعلّم على قيمة منخفضة جدًا، سيستغرق التدريب وقتًا طويلاً جدًا. إذا حدّدت معدّل التعلّم على قيمة مرتفعة جدًا، سيواجه نزول التدرّج غالبًا صعوبة في الوصول إلى التقارب.
يمكنك الاطّلاع على الانحدار الخطي: المَعلمات الفائقة في "دورة مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
خطي
يشير ذلك المصطلح إلى علاقة بين متغيّرَين أو أكثر يمكن تمثيلها فقط من خلال الجمع والضرب.
رسم العلاقة الخطية هو خط.
يجب أن يكون التباين غير خطي.
النموذج الخطي
النموذج الذي يحدّد وزنًا واحدًا لكل سمة لإجراء توقّعات (تتضمّن النماذج الخطية أيضًا انحيازًا). في المقابل، تكون العلاقة بين الميزات والتوقعات في النماذج العميقة غير خطية بشكل عام.
عادةً ما يكون تدريب النماذج الخطية أسهل وأكثر قابلية للتفسير من النماذج العميقة. ومع ذلك، يمكن للنماذج العميقة التعرّف على العلاقات المعقّدة بين الميزات.
الانحدار الخطي والانحدار اللوجستي هما نوعان من النماذج الخطية.
الانحدار الخطي
نوع من نماذج تعلُّم الآلة ينطبق عليه ما يلي:
قارِن الانحدار الخطي بالانحدار اللوجستي. قارِن أيضًا بين الانحدار والتصنيف.
يمكنك الاطّلاع على الانحدار الخطي في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
الانحدار اللوجستي
نوع من نماذج الانحدار التي تتوقّع احتمالية. تتضمّن نماذج الانحدار اللوجستي الخصائص التالية:
- التصنيف فئوي. يشير مصطلح الانحدار اللوجستي عادةً إلى الانحدار اللوجستي الثنائي، أي إلى نموذج يحسب احتمالات التصنيفات التي تتضمّن قيمتَين محتملتَين. هناك صيغة أقل شيوعًا، وهي الانحدار اللوجستي المتعدد الحدود، التي تحسب احتمالات التصنيفات التي تتضمّن أكثر من قيمتَين محتملتَين.
- دالة الخسارة أثناء التدريب هي الخسارة اللوغاريتمية. (يمكن وضع وحدات Log Loss متعددة بالتوازي للتصنيفات التي تتضمّن أكثر من قيمتَين محتملتَين).
- يستخدم النموذج بنية خطية، وليس شبكة عصبية عميقة. ومع ذلك، ينطبق الجزء المتبقي من هذا التعريف أيضًا على النماذج العميقة التي تتنبأ بالاحتمالات للتصنيفات الفئوية.
على سبيل المثال، لنفترض نموذج انحدار لوجستي يحسب احتمال أن تكون رسالة إلكترونية واردة غير مرغوب فيها أو غير ذلك. أثناء الاستدلال، لنفترض أنّ النموذج يتوقّع القيمة 0.72. وبالتالي، يقدّر النموذج ما يلي:
- فرصة بنسبة% 72 أن تكون الرسالة الإلكترونية غير مرغوب فيها
- هناك احتمال بنسبة% 28 ألّا تكون الرسالة الإلكترونية غير مرغوب فيها.
يستخدم نموذج الانحدار اللوجستي البنية التالية المكوّنة من خطوتَين:
- ينشئ النموذج قيمة توقّع أولية (y') من خلال تطبيق دالة خطية على ميزات الإدخال.
- يستخدم النموذج هذا التوقّع الأولي كإدخال إلى دالة سينية، ما يؤدي إلى تحويل التوقّع الأولي إلى قيمة بين 0 و1، باستثناء هذين الرقمين.
كما هو الحال مع أي نموذج انحدار، يتنبأ نموذج الانحدار اللوجستي برقم. ومع ذلك، يصبح هذا الرقم عادةً جزءًا من نموذج تصنيف ثنائي على النحو التالي:
- إذا كان الرقم المتوقّع أكبر من حد التصنيف، سيتوقّع نموذج التصنيف الثنائي الفئة الإيجابية.
- إذا كان الرقم المتوقّع أقل من حد التصنيف، يتوقّع نموذج التصنيف الثنائي الفئة السلبية.
لمزيد من المعلومات، يمكنك الاطّلاع على الانحدار اللوجستي في "دورة مكثّفة عن تعلّم الآلة".
الخسارة اللوغاريتمية
دالة الخسارة المستخدَمة في الانحدار اللوجستي الثنائي
يمكنك الاطّلاع على الانحدار اللوجستي: الخسارة والتسوية في "دورة تدريبية مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
لوغاريتم فرص الأفضلية
يشير ذلك المصطلح إلى لوغاريتم يوضِّح معدّل احتمالية وقوع حدث معيّن.
خسارة
أثناء تدريب نموذج خاضع للإشراف، يتم قياس مدى بُعد توقّع النموذج عن تصنيفه.
تحسب دالة الخسارة الخسارة.
يمكنك الاطّلاع على الانحدار الخطي: الخسارة في "الدورة التدريبية المكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
منحنى الخسارة
رسم بياني للخطأ كدالة لعدد التكرارات أثناء التدريب يعرض الرسم البياني التالي منحنى خسارة نموذجيًا:
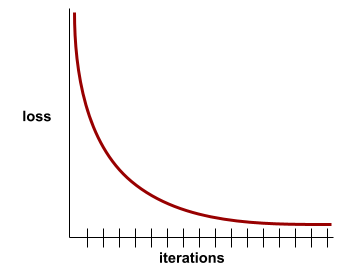
يمكن أن تساعدك منحنيات الخسارة في تحديد ما إذا كان نموذجك يتقارب أو يفرط في التكيّف.
يمكن أن ترسم منحنيات الخسارة جميع أنواع الخسارة التالية:
يمكنك أيضًا الاطّلاع على منحنى التعميم.
يمكنك الاطّلاع على التدريب الزائد: تفسير منحنيات الخسارة في "دورة مكثّفة عن تعلُّم الآلة" للحصول على مزيد من المعلومات.
دالة الخسارة
أثناء التدريب أو الاختبار، يتم استخدام دالة رياضية تحسب مقدار الخطأ في دفعة من الأمثلة. تعرض دالة الخسارة قيمة خسارة أقل للنماذج التي تقدّم توقعات جيدة مقارنةً بالنماذج التي تقدّم توقعات سيئة.
عادةً ما يكون الهدف من التدريب هو تقليل الخسارة التي تعرضها دالة الخسارة.
تتوفّر العديد من أنواع دوال الخسارة المختلفة. اختَر دالة الخسارة المناسبة لنوع النموذج الذي تنشئه. على سبيل المثال:
- فقدانL (أو متوسط الخطأ التربيعي) هو دالة الفقدان للانحدار الخطي.
- الخسارة اللوغاريتمية هي دالة الخسارة الخاصة بالانحدار اللوجستي.
M
تعلُم الآلة
برنامج أو نظام يدرّب نموذجًا من البيانات التي يتم إدخالها. يمكن للنموذج المدرَّب أن يقدّم توقّعات مفيدة من بيانات جديدة (لم يسبق رؤيتها) مأخوذة من التوزيع نفسه المستخدَم لتدريب النموذج.
يشير تعلُّم الآلة أيضًا إلى مجال الدراسة المعني بهذه البرامج أو الأنظمة.
يمكنك الاطّلاع على دورة مقدّمة عن تعلُّم الآلة للحصول على مزيد من المعلومات.
الفئة الأكبر
التصنيف الأكثر شيوعًا في مجموعة بيانات غير متوازنة الفئات على سبيل المثال، إذا كانت مجموعة البيانات تحتوي على 99% من التصنيفات السلبية و1% من التصنيفات الإيجابية، تكون التصنيفات السلبية هي الفئة الأكبر.
التباين مع الفئة الأقلية
يمكنك الاطّلاع على مجموعات البيانات: مجموعات البيانات غير المتوازنة في "الدورة التدريبية المكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
دفعة صغيرة
مجموعة فرعية صغيرة يتم اختيارها عشوائيًا من دفعة تتم معالجتها في تكرار واحد. يتراوح حجم الدفعة للدفعة المصغّرة عادةً بين 10 و1,000 مثال.
على سبيل المثال، لنفترض أنّ مجموعة التدريب الكاملة (الدفعة الكاملة) تتألف من 1,000 مثال. لنفترض أيضًا أنّك ضبطت حجم الدفعة لكل دفعة صغيرة على 20. لذلك، تحدّد كل تكرار الخسارة في 20 مثالاً عشوائيًا من بين 1,000 مثال، ثم تعدّل الأوزان والانحيازات وفقًا لذلك.
من الأسهل بكثير حساب الخسارة على مجموعة مصغّرة من البيانات مقارنةً بحساب الخسارة على جميع الأمثلة في المجموعة الكاملة.
يمكنك الاطّلاع على الانحدار الخطي: المَعلمات الفائقة في "دورة مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
فئة الأقلية
التصنيف الأقل شيوعًا في مجموعة بيانات غير متوازنة على سبيل المثال، إذا كانت مجموعة البيانات تحتوي على% 99 من التصنيفات السلبية و% 1 من التصنيفات الإيجابية، تكون التصنيفات الإيجابية هي الفئة الأقلية.
التباين مع الفئة الأغلبية
يمكنك الاطّلاع على مجموعات البيانات: مجموعات البيانات غير المتوازنة في "الدورة التدريبية المكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
نموذج
بشكل عام، أي صيغة رياضية تعالج البيانات المدخلة وتعرض الناتج. بعبارة أخرى، النموذج هو مجموعة المَعلمات والبنية اللازمة لنظام ما من أجل وضع التوقعات. في تعلُّم الآلة الموجَّه، يتلقّى النموذج مثالاً كمدخل ويستنتج توقّعًا كمخرج. تختلف النماذج بعض الشيء ضمن تعلُّم الآلة الموجَّه. على سبيل المثال:
- يتألف نموذج الانحدار الخطي من مجموعة من الأوزان والانحياز.
- يتألف نموذج الشبكة العصبونية مما يلي:
- مجموعة من الطبقات المخفية، تحتوي كل منها على عصبون واحد أو أكثر
- الأوزان والانحياز المرتبط بكل عصبون
- يتألف نموذج شجرة القرار مما يلي:
- شكل الشجرة، أي النمط الذي يتم فيه ربط الشروط والأوراق.
- الشروط والإجازات
يمكنك حفظ نموذج أو استعادته أو إنشاء نُسخ منه.
تؤدي عملية تعلُّم الآلة غير الموجَّه أيضًا إلى إنشاء نماذج، وهي عادةً عبارة عن دالة يمكنها ربط مثال إدخال بالمجموعة الأنسب.
التصنيف المتعدّد الفئات
في التعلّم المُوجّه، تكون هناك مشكلة تصنيف حيث تحتوي مجموعة البيانات على أكثر من فئتَين من التصنيفات. على سبيل المثال، يجب أن تكون التصنيفات في مجموعة بيانات Iris إحدى الفئات الثلاث التالية:
- Iris setosa
- Iris virginica
- Iris versicolor
النموذج الذي تم تدريبه على مجموعة بيانات Iris والذي يتوقّع نوع Iris استنادًا إلى أمثلة جديدة، يؤدي عملية تصنيف متعدّد الفئات.
في المقابل، فإنّ مشاكل التصنيف التي تميّز بين فئتَين بالضبط هي نماذج تصنيف ثنائي. على سبيل المثال، نموذج البريد الإلكتروني الذي يتوقّع ما إذا كانت الرسالة غير مرغوب فيها أو مرغوب فيها هو نموذج تصنيف ثنائي.
في مشاكل التجميع، يشير التصنيف المتعدد الفئات إلى أكثر من مجموعتين.
لمزيد من المعلومات، يمكنك الاطّلاع على الشبكات العصبية: التصنيف المتعدد الفئات في "الدورة التدريبية المكثّفة حول تعلُّم الآلة".
لا
فئة سالبة
في التصنيف الثنائي، يُطلق على إحدى الفئتَين اسم إيجابية ويُطلق على الأخرى اسم سلبية. الفئة الإيجابية هي الشيء أو الحدث الذي يختبره النموذج، والفئة السلبية هي الاحتمال الآخر. على سبيل المثال:
- قد تكون الفئة السلبية في اختبار طبي هي "ليس ورمًا".
- قد تكون الفئة السلبية في نموذج تصنيف الرسائل الإلكترونية هي "ليست رسالة غير مرغوب فيها".
يجب التمييز بينها وبين الفئة الموجبة.
شبكة عصبونية
نموذج يحتوي على طبقة مخفية واحدة على الأقل. الشبكة العصبية العميقة هي نوع من الشبكات العصبية يحتوي على أكثر من طبقة مخفية واحدة. على سبيل المثال، يعرض المخطط التالي شبكة عصبية عميقة تحتوي على طبقتَين مخفيتَين.
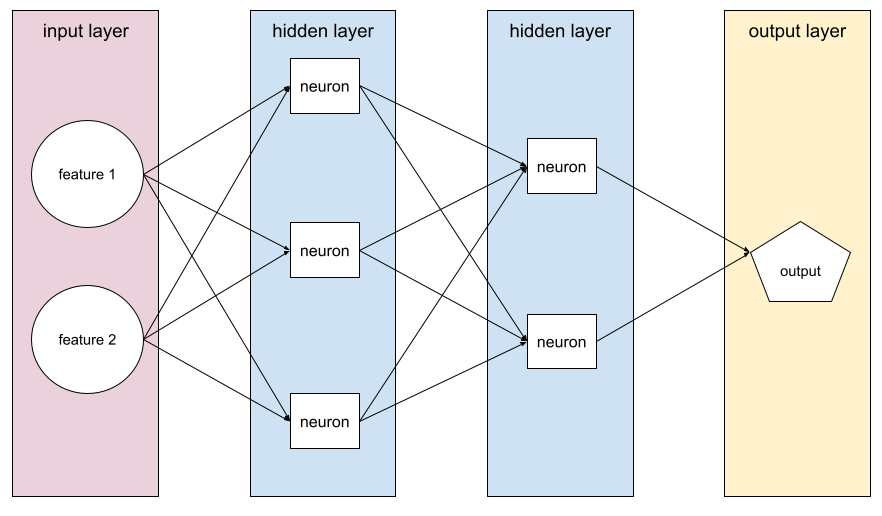
يتصل كل عصبون في الشبكة العصبية بجميع العُقد في الطبقة التالية. على سبيل المثال، في الرسم البياني السابق، لاحظ أنّ كل عصبون من الأعصاب الثلاثة في الطبقة المخفية الأولى يرتبط بشكل منفصل بكل من العصبونين في الطبقة المخفية الثانية.
تُعرف الشبكات العصبونية التي يتم تنفيذها على أجهزة الكمبيوتر أحيانًا باسم الشبكات العصبونية الاصطناعية للتمييز بينها وبين الشبكات العصبونية الموجودة في الدماغ والجهاز العصبي.
يمكن لبعض الشبكات العصبية محاكاة العلاقات غير الخطية المعقّدة للغاية بين الميزات المختلفة والتصنيف.
راجِع أيضًا الشبكة العصبونية الالتفافية والشبكة العصبونية المتكرّرة.
يمكنك الاطّلاع على الشبكات العصبونية في "دورة مكثّفة عن تعلّم الآلة" لمزيد من المعلومات.
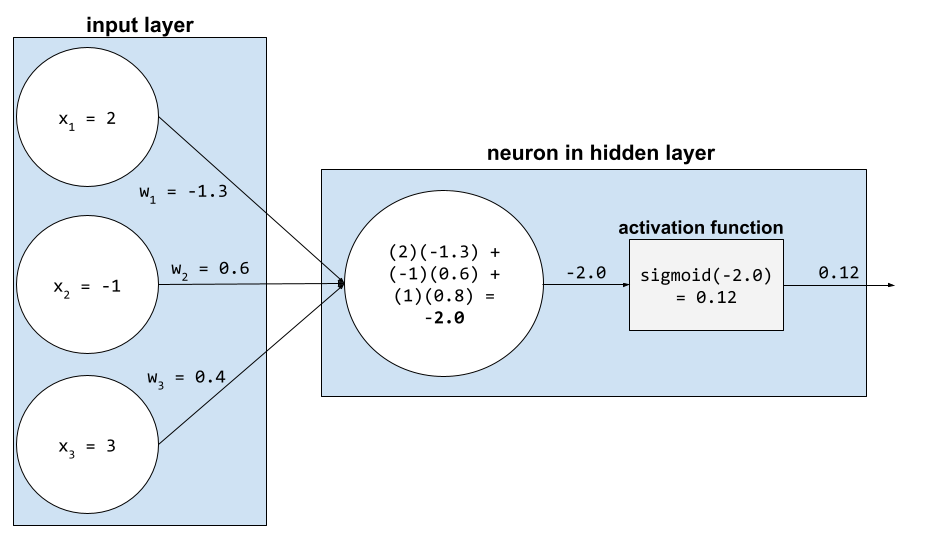
عصبون
في تعلُّم الآلة، هي وحدة مميّزة ضمن طبقة مخفية في شبكة عصبونية. تنفّذ كل خلية عصبية الإجراء المكوّن من خطوتَين التاليتَين:
- تحسب هذه الدالة المجموع المرجّح لقيم الإدخال مضروبة في الأوزان المقابلة.
- تمرير المجموع المرجّح كمدخل إلى دالة التنشيط
تقبل إحدى الخلايا العصبية في الطبقة المخفية الأولى مدخلات من قيم الميزات في طبقة الإدخال. تتلقّى الخلية العصبية في أي طبقة مخفية بعد الطبقة الأولى مدخلات من الخلايا العصبية في الطبقة المخفية السابقة. على سبيل المثال، تقبل إحدى الخلايا العصبية في الطبقة المخفية الثانية المدخلات من الخلايا العصبية في الطبقة المخفية الأولى.
توضّح الصورة التالية خليتَين عصبيتين ومدخلاتهما.
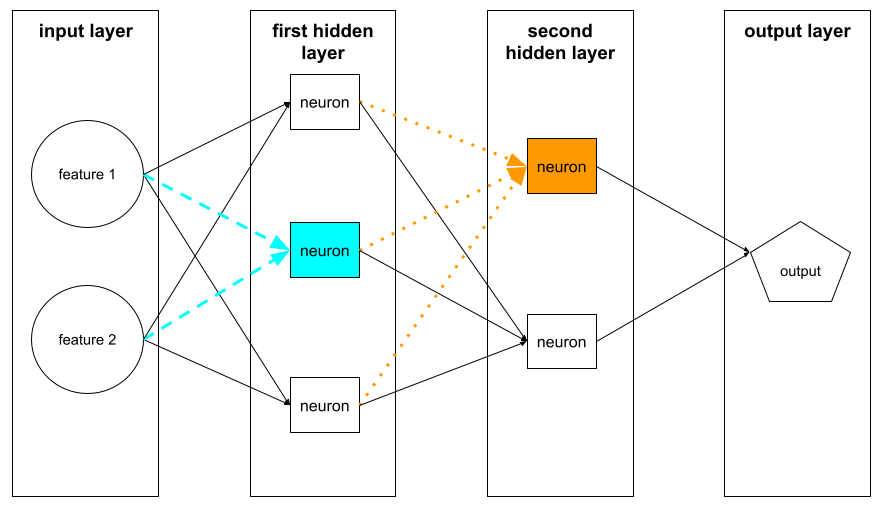
تحاكي الخلية العصبية في الشبكة العصبونية سلوك الخلايا العصبية في الدماغ وأجزاء أخرى من الجهاز العصبي.
عقدة (شبكة عصبونية)
عصبون في طبقة مخفية
يمكنك الاطّلاع على الشبكات العصبونية في "دورة مكثّفة عن تعلّم الآلة" لمزيد من المعلومات.
غير خطي
يشير ذلك المصطلح إلى علاقة بين متغيّرَين أو أكثر لا يمكن تمثيلها فقط من خلال الجمع والضرب. يمكن تمثيل العلاقة الخطية بخط، بينما لا يمكن تمثيل العلاقة غير الخطية بخط. على سبيل المثال، لنفترض أنّ لديك نموذجين يرتبط كل منهما بميزة واحدة وتصنيف واحد. النموذج على اليمين خطي، والنموذج على اليسار غير خطي:

راجِع الشبكات العصبية: العُقد والطبقات المخفية في "دورة تدريبية مكثّفة حول تعلُّم الآلة" لتجربة أنواع مختلفة من الدوال غير الخطية.
عدم الثبات
هي سمة تتغيّر قيمها على مستوى سمة واحدة أو أكثر، وعادةً ما تكون هذه السمة هي الوقت. على سبيل المثال، إليك بعض الأمثلة على عدم الثبات:
- يختلف عدد ملابس السباحة التي يتم بيعها في متجر معيّن حسب الموسم.
- إنّ كمية الفاكهة المعيّنة التي يتم حصادها في منطقة معيّنة تكون صفرًا خلال معظم أوقات السنة، ولكنها تكون كبيرة خلال فترة قصيرة.
- بسبب تغيّر المناخ، تتغيّر متوسطات درجات الحرارة السنوية.
التباين مع الثبات
التسوية
بشكل عام، تشير عملية تحويل النطاق الفعلي لقيم أحد المتغيّرات إلى نطاق قياسي من القيم، مثل:
- من -1 إلى +1
- من 0 إلى 1
- الدرجات المعيارية (من -3 إلى +3 تقريبًا)
على سبيل المثال، لنفترض أنّ النطاق الفعلي لقيم ميزة معيّنة هو 800 إلى 2,400. كجزء من هندسة الميزات، يمكنك تسوية القيم الفعلية إلى نطاق عادي، مثل من -1 إلى +1.
التسوية هي مهمة شائعة في هندسة الميزات. تتدرب النماذج عادةً بشكل أسرع (وتنتج توقعات أفضل) عندما يكون لكل ميزة رقمية في متّجه الميزات النطاق نفسه تقريبًا.
راجِع أيضًا التسوية باستخدام درجة Z.
لمزيد من المعلومات، راجِع البيانات الرقمية: التسوية في "الدورة التدريبية المكثّفة حول تعلُّم الآلة".
بيانات رقمية
الميزات الممثَّلة كأعداد صحيحة أو أرقام ذات قيم حقيقية على سبيل المثال، من المرجّح أن يعرض نموذج تقييم منزل مساحة المنزل (بالقدم المربع أو المتر المربع) كبيانات رقمية. يشير تمثيل إحدى السمات كبيانات رقمية إلى أنّ قيم السمة لها علاقة رياضية بالتصنيف. أي أنّ عدد الأمتار المربعة في المنزل يرتبط على الأرجح بعلاقة رياضية بقيمة المنزل.
لا يجب تمثيل جميع بيانات الأعداد الصحيحة كبيانات رقمية. على سبيل المثال، الرموز البريدية في بعض أنحاء العالم هي أعداد صحيحة، ولكن لا يجب تمثيل الرموز البريدية التي تتضمّن أعدادًا صحيحة كبيانات رقمية في النماذج. ذلك لأنّ الرمز البريدي 20000 ليس ضعف (أو نصف) فعالية الرمز البريدي 10000. بالإضافة إلى ذلك، على الرغم من أنّ الرموز البريدية المختلفة مرتبطة بقيم مختلفة للعقارات، لا يمكننا افتراض أنّ قيم العقارات في الرمز البريدي 20000 هي ضعف قيم العقارات في الرمز البريدي 10000.
بدلاً من ذلك، يجب تمثيل الرموز البريدية على أنّها بيانات فئوية.
يُطلق على الميزات الرقمية أحيانًا اسم الميزات المستمرة.
لمزيد من المعلومات، راجِع التعامل مع البيانات الرقمية في "الدورة التدريبية المكثّفة حول تعلُّم الآلة".
O
بلا إنترنت
مرادف ثابت
الاستنتاج المؤخَّر
تشير إلى عملية إنشاء نموذج لمجموعة من التوقّعات ثم تخزين هذه التوقّعات مؤقتًا (حفظها). يمكن للتطبيقات بعد ذلك الوصول إلى التوقّع المستنتَج من ذاكرة التخزين المؤقت بدلاً من إعادة تشغيل النموذج.
على سبيل المثال، لنفترض أنّ هناك نموذجًا ينشئ توقّعات أحوال الطقس المحلية (توقّعات) مرة كل أربع ساعات. بعد كل عملية تشغيل للنموذج، يخزّن النظام مؤقتًا جميع توقّعات الطقس المحلية. تسترجع تطبيقات الطقس التوقعات من ذاكرة التخزين المؤقت.
يُطلق على الاستنتاج بلا إنترنت أيضًا اسم الاستنتاج الثابت.
يختلف ذلك عن الاستدلال على الإنترنت. يمكنك الاطّلاع على أنظمة تعلُّم الآلة في مرحلة الإنتاج: الاستنتاج الثابت مقابل الاستنتاج الديناميكي في "دورة تدريبية مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
الترميز الأحادي
تمثيل البيانات الفئوية كمتّجه حيث:
- يتم ضبط أحد العناصر على 1.
- ويتم ضبط جميع العناصر الأخرى على 0.
يُستخدَم الترميز النشط الواحد بشكل شائع لتمثيل السلاسل أو المعرّفات التي تتضمّن مجموعة محدودة من القيم المحتملة.
على سبيل المثال، لنفترض أنّ هناك ميزة فئوية معيّنة باسم Scandinavia لها خمس قيم محتملة:
- "الدنمارك"
- "السويد"
- "النرويج"
- فنلندا ("Finland")
- "آيسلندا"
يمكن أن يمثّل الترميز الأحادي الساخن كل قيمة من القيم الخمس على النحو التالي:
| البلد | المتّجه | ||||
|---|---|---|---|---|---|
| "الدنمارك" | 1 | 0 | 0 | 0 | 0 |
| "السويد" | 0 | 1 | 0 | 0 | 0 |
| "النرويج" | 0 | 0 | 1 | 0 | 0 |
| فنلندا ("Finland") | 0 | 0 | 0 | 1 | 0 |
| "آيسلندا" | 0 | 0 | 0 | 0 | 1 |
بفضل الترميز الأحادي الساخن، يمكن للنموذج التعرّف على روابط مختلفة استنادًا إلى كل بلد من البلدان الخمسة.
تمثيل ميزة كبيانات رقمية هو بديل للترميز الأحادي. للأسف، لا يُعد تمثيل البلدان الإسكندنافية رقميًا خيارًا جيدًا. على سبيل المثال، ضع في اعتبارك التمثيل الرقمي التالي:
- "الدنمارك" هي 0
- "السويد" هي 1
- "النرويج" هي 2
- "فنلندا" هي 3
- "آيسلندا" هي 4
باستخدام الترميز الرقمي، سيفسّر النموذج الأرقام الأولية رياضيًا وسيحاول التدريب على هذه الأرقام. ومع ذلك، لا يبلغ عدد سكان آيسلندا ضعف عدد سكان النرويج (أو نصفه)، لذا سيتوصّل النموذج إلى بعض الاستنتاجات الغريبة.
لمزيد من المعلومات، يُرجى الاطّلاع على البيانات الفئوية: المفردات والترميز الساخن في "الدورة التدريبية المكثّفة حول تعلُّم الآلة".
واحد-مقابل-الكل
في حال توفّر مشكلة تصنيف تتضمّن N فئة، يكون الحلّ عبارة عن نموذج تصنيف ثنائي منفصل يتضمّن N فئة، أي نموذج تصنيف ثنائي لكل نتيجة محتملة. على سبيل المثال، إذا كان لديك نموذج يصنّف الأمثلة على أنّها حيوان أو نبات أو معدن، سيقدّم الحلّ القائم على مقارنة كل فئة بباقي الفئات النماذج الثلاثة المنفصلة التالية للتصنيف الثنائي:
- حيوان أو ليس حيوانًا
- خضار أو غير خضار
- معدني وغير معدني
online
مرادف لكلمة ديناميكي
الاستنتاج الحي
إنشاء توقّعات عند الطلب على سبيل المثال، لنفترض أنّ تطبيقًا يمرّر بيانات إلى نموذج ويصدر طلبًا للحصول على نتيجة متوقّعة. يستجيب النظام الذي يستخدم الاستدلال على الإنترنت للطلب من خلال تشغيل النموذج (وعرض التوقّع للتطبيق).
يختلف ذلك عن الاستدلال بلا إنترنت.
يمكنك الاطّلاع على أنظمة تعلُّم الآلة في مرحلة الإنتاج: الاستنتاج الثابت مقابل الاستنتاج الديناميكي في "دورة تدريبية مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
طبقة الإخراج
الطبقة "النهائية" في الشبكة العصبية تحتوي طبقة الإخراج على التوقّع.
يوضّح الرسم التوضيحي التالي شبكة عصبية عميقة صغيرة تتضمّن طبقة إدخال وطبقتَين مخفيتَين وطبقة إخراج:
فرط التخصيص
إنشاء نموذج يطابق بيانات التدريب بشكل كبير جدًا، ما يؤدي إلى عدم قدرة النموذج على تقديم توقّعات صحيحة بشأن البيانات الجديدة
يمكن أن يؤدي التسوية إلى الحدّ من الإفراط في التكيّف. يمكن أن يؤدي التدريب على مجموعة تدريب كبيرة ومتنوعة أيضًا إلى تقليل الإفراط في التخصيص.
يمكنك الاطّلاع على الإفراط في التخصيص في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
P
باندا
واجهة برمجة تطبيقات لتحليل البيانات موجّهة نحو الأعمدة ومصمَّمة استنادًا إلى numpy. تتيح العديد من أُطر عمل تعلُّم الآلة، بما في ذلك TensorFlow، استخدام بنى بيانات pandas كمدخلات. لمزيد من التفاصيل، يُرجى الاطّلاع على مستندات pandas.
مَعلمة
الأوزان والانحيازات التي يتعلّمها النموذج أثناء التدريب على سبيل المثال، في نموذج الانحدار الخطي، تتألف المَعلمات من الانحياز (b) وجميع الأوزان (w1 وw2 وما إلى ذلك) في الصيغة التالية:
في المقابل، فرط المعلمات هي القيم التي توفّرها أنت (أو خدمة ضبط فرط المعلمات) للنموذج. على سبيل المثال، معدّل التعلّم هو وسيط فائق.
فئة موجبة
الفئة التي تختبرها.
على سبيل المثال، قد تكون الفئة الموجبة في نموذج السرطان هي "ورم". قد تكون الفئة الإيجابية في نموذج تصنيف رسائل إلكترونية هي "رسائل غير مرغوب فيها".
يجب التمييز بينها وبين الفئة السلبية.
المعالجة اللاحقة
تعديل ناتج النموذج بعد تشغيله يمكن استخدام المعالجة اللاحقة لفرض قيود الإنصاف بدون تعديل النماذج نفسها.
على سبيل المثال، يمكن تطبيق المعالجة اللاحقة على نموذج التصنيف الثنائي من خلال ضبط حدّ التصنيف، وذلك للحفاظ على تكافؤ الفرص لبعض السمات من خلال التأكّد من أنّ معدّل الإيجابية الحقيقية هو نفسه لجميع قيم تلك السمة.
الدقة
مقياس لنماذج التصنيف يجيب عن السؤال التالي:
عندما توقّع النموذج الفئة الموجبة، ما هي النسبة المئوية للتوقّعات الصحيحة؟
في ما يلي الصيغة:
where:
- تعني النتيجة الإيجابية الصحيحة أنّ النموذج توقّع بشكلٍ صحيح الفئة الإيجابية.
- تعني النتيجة الموجبة الخاطئة أنّ النموذج توقّع بشكل خاطئ الفئة الموجبة.
على سبيل المثال، لنفترض أنّ نموذجًا قدّم 200 توقّع إيجابي. من بين هذه التوقّعات الإيجابية البالغ عددها 200:
- كانت 150 منها نتائج موجبة صحيحة.
- كانت 50 منها نتائج موجبة خاطئة.
في هذه الحالة:
يجب التمييز بين هذا المقياس ومقياسَي الدقة واكتمال التوقعات الإيجابية.
يمكنك الاطّلاع على التصنيف: الدقة والاسترجاع والضبط والمقاييس ذات الصلة في "دورة تدريبية مكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.
التوقّع
ناتج النموذج على سبيل المثال:
- يكون التوقّع الذي يقدّمه نموذج التصنيف الثنائي إما الفئة الإيجابية أو الفئة السلبية.
- التصنيف الذي يتوقّعه نموذج التصنيف المتعدد الفئات هو فئة واحدة.
- توقّع نموذج الانحدار الخطي هو رقم.
تصنيفات تقريبية
البيانات المستخدَمة لتقريب التصنيفات غير المتوفّرة مباشرةً في مجموعة البيانات
على سبيل المثال، لنفترض أنّه عليك تدريب نموذج للتنبؤ بمستوى الإجهاد لدى الموظفين. تحتوي مجموعة البيانات على الكثير من الميزات التنبؤية، ولكنها لا تتضمّن تصنيفًا باسم مستوى الإجهاد. لم يثنِك ذلك عن اختيار "حوادث في مكان العمل" كبديل لمستوى الإجهاد. ففي النهاية، يتعرّض الموظفون الذين يعانون من ضغط كبير إلى حوادث أكثر من الموظفين الذين يتمتعون بالهدوء. أم أنّها كذلك؟ ربما تزداد حوادث العمل وتنخفض لأسباب متعددة.
كمثال ثانٍ، لنفترض أنّك تريد أن تكون هل تمطر؟ تصنيفًا منطقيًا لمجموعة البيانات، ولكنّ مجموعة البيانات لا تحتوي على بيانات حول المطر. إذا كانت الصور الفوتوغرافية متاحة، يمكنك إنشاء تصنيف بديل لـ هل تمطر؟ من خلال عرض صور لأشخاص يحملون مظلات. هل هذا تصنيف تقريبي جيد؟ من المحتمل ذلك، ولكن قد يميل الأشخاص في بعض الثقافات إلى حمل المظلات للحماية من الشمس أكثر من الحماية من المطر.
غالبًا ما تكون التصنيفات البديلة غير مثالية. عند الإمكان، اختَر التصنيفات الفعلية بدلاً من التصنيفات البديلة. مع ذلك، عند عدم توفّر تصنيف فعلي، يجب اختيار التصنيف البديل بعناية فائقة، مع الحرص على اختيار التصنيف البديل الأقل سوءًا.
لمزيد من المعلومات، اطّلِع على مجموعات البيانات: التصنيفات في "دورة مكثّفة عن تعلُّم الآلة".
R
التوليد المعزّز بالاسترجاع (RAG)
اختصار التوليد المعزّز بالاسترجاع
مُصنِّف
هو شخص يقدّم تصنيفات لأمثلة. "المعلِّق" هو اسم آخر للمقيّم.
لمزيد من المعلومات، اطّلِع على البيانات الفئوية: المشاكل الشائعة في "الدورة التدريبية المكثّفة حول تعلُّم الآلة".
تذكُّر الإعلان
مقياس لنماذج التصنيف يجيب عن السؤال التالي:
عندما كانت الحقيقة الأساسية هي الفئة الموجبة، ما هي النسبة المئوية للتوقعات التي حدّدها النموذج بشكل صحيح على أنّها الفئة الموجبة؟
في ما يلي الصيغة:
\[\text{Recall} = \frac{\text{true positives}} {\text{true positives} + \text{false negatives}} \]
where:
- تعني النتيجة الإيجابية الصحيحة أنّ النموذج توقّع بشكلٍ صحيح الفئة الإيجابية.
- يعني السلبي الخاطئ أنّ النموذج توقّع بشكل خاطئ الفئة السلبية.
على سبيل المثال، لنفترض أنّ نموذجك قدّم 200 توقّع بشأن أمثلة كانت الحقيقة الأساسية فيها هي الفئة الموجبة. من بين هذه التوقعات الـ 200:
- كانت 180 منها نتائج موجبة صحيحة.
- كانت 20 منها نتائج سلبية خاطئة.
في هذه الحالة:
\[\text{Recall} = \frac{\text{180}} {\text{180} + \text{20}} = 0.9 \]
يمكنك الاطّلاع على التصنيف: الدقة والاسترجاع والضبط والمقاييس ذات الصلة للحصول على مزيد من المعلومات.
وحدة خطية مصحَّحة (ReLU)
دالّة تفعيل ذات السلوك التالي:
- إذا كان الإدخال سالبًا أو صفرًا، يكون الناتج 0.
- إذا كانت القيمة المدخلة موجبة، تكون القيمة الناتجة مساوية للقيمة المدخلة.
على سبيل المثال:
- إذا كان المُدخل -3، يكون الناتج 0.
- إذا كانت القيمة المُدخَلة هي +3، تكون القيمة الناتجة هي 3.0.
في ما يلي رسم بياني لدالة ReLU:
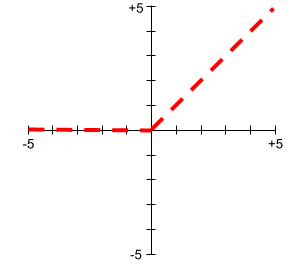
ReLU هي دالة تنشيط شائعة جدًا. على الرغم من سلوكها البسيط، تتيح دالة ReLU للشبكة العصبية تعلُّم العلاقات غير الخطية بين الميزات والتصنيف.
نموذج الانحدار
بشكل غير رسمي، هو نموذج ينشئ توقّعًا رقميًا. (في المقابل، ينشئ نموذج التصنيف توقعًا للفئة). على سبيل المثال، جميع ما يلي هي نماذج انحدار:
- نموذج يتوقّع قيمة منزل معيّن باليورو، مثل 423,000.
- نموذج يتوقّع متوسط العمر المتوقّع لشجرة معيّنة بالسنوات، مثل 23.2.
- نموذج يتوقّع كمية الأمطار التي ستتساقط بالبوصة في مدينة معيّنة خلال الساعات الست القادمة، مثل 0.18.
في ما يلي نوعان شائعان من نماذج الانحدار:
- الانحدار الخطي: يجد هذا النموذج الخط الذي يطابق قيم التصنيفات مع الميزات على أفضل وجه.
- الانحدار اللوجستي، الذي ينشئ احتمالية تتراوح بين 0.0 و1.0، ثم يربطها النظام عادةً بتوقّع فئة.
ليس كل نموذج يعرض توقّعات عددية هو نموذج انحدار. في بعض الحالات، يكون التوقّع الرقمي مجرّد نموذج تصنيف يحتوي على أسماء فئات رقمية. على سبيل المثال، النموذج الذي يتوقّع رمزًا بريديًا رقميًا هو نموذج تصنيف، وليس نموذج انحدار.
التسوية
أي آلية تقلّل من التطابق الزائد تشمل الأنواع الشائعة من التسوية ما يلي:
- L1 regularization
- التسوية 2
- تسوية الإسقاط
- التوقّف المبكر (هذه ليست طريقة تسوية رسمية، ولكن يمكن أن تحدّ بشكل فعّال من الإفراط في التكيّف)
يمكن أيضًا تعريف التسوية على أنّها العقوبة المفروضة على تعقيد النموذج.
لمزيد من المعلومات، يُرجى الاطّلاع على الإفراط في التكيّف: تعقيد النموذج في "الدورة التدريبية المكثّفة حول تعلُّم الآلة".
معدّل التسوية
رقم يحدّد الأهمية النسبية للتسوية أثناء التدريب. تؤدي زيادة معدّل التسوية إلى الحدّ من التطابق الزائد، ولكنها قد تقلّل من قدرة النموذج على التوقّع. في المقابل، يؤدي تقليل معدّل التسوية أو إغفاله إلى زيادة الملاءمة الزائدة.
لمزيد من المعلومات، يمكنك الاطّلاع على الإفراط في التخصيص: التسوية L2 في "دورة مكثّفة حول تعلُّم الآلة".
ReLU
اختصار الوحدة الخطية المصحَّحة
التوليد المعزّز بالاسترجاع (RAG)
يشير ذلك إلى أسلوب لتحسين جودة النتائج التي تقدّمها النماذج اللغوية الكبيرة من خلال ربطها بمصادر المعلومات التي تم استرجاعها بعد تدريب النموذج. يحسّن التوليد المعزّز بالاسترجاع دقة ردود النماذج اللغوية الكبيرة من خلال منح النموذج اللغوي الكبير المدرَّب إمكانية الوصول إلى المعلومات التي يتم استرجاعها من قواعد المعرفة أو المستندات الموثوقة.
تشمل الدوافع الشائعة لاستخدام التوليد المعزّز بالاسترجاع ما يلي:
- زيادة الدقة الواقعية للردود التي ينشئها النموذج
- منح النموذج إذن الوصول إلى معلومات لم يتم تدريبه عليها
- تغيير المعرفة التي يستخدمها النموذج
- تمكين النموذج من الاستشهاد بالمصادر
على سبيل المثال، لنفترض أنّ تطبيقًا للكيمياء يستخدم واجهة برمجة التطبيقات PaLM لإنشاء ملخّصات ذات صلة بطلبات بحث المستخدمين. عندما يتلقّى الخلفية في التطبيق طلب بحث، تقوم الخلفية بما يلي:
- يبحث عن البيانات ذات الصلة بطلب بحث المستخدم ("يسترجعها").
- يضيف ("يعزّز") بيانات الكيمياء ذات الصلة إلى طلب بحث المستخدم.
- يطلب من النموذج اللغوي الكبير إنشاء ملخّص استنادًا إلى البيانات الملحقة.
منحنى الأمثلة الإيجابية
رسم بياني لمعدّل الموجب الصحيح مقابل معدّل الموجب الخاطئ لقيم مختلفة لحدود التصنيف في التصنيف الثنائي.
يشير شكل منحنى ROC إلى قدرة نموذج التصنيف الثنائي على فصل الفئات الإيجابية عن الفئات السلبية. لنفترض مثلاً أنّ نموذج تصنيف ثنائي يفصل تمامًا بين جميع الفئات السلبية وجميع الفئات الإيجابية:
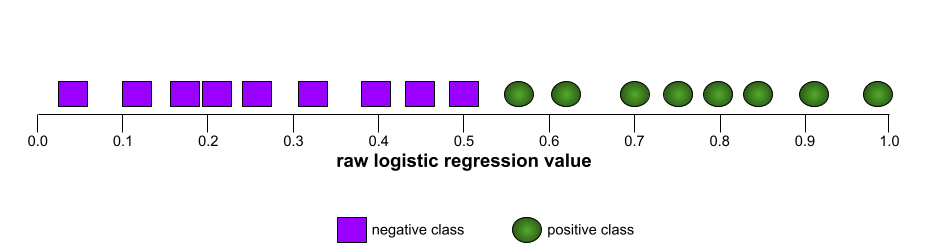
يبدو منحنى ROC للنموذج السابق على النحو التالي:
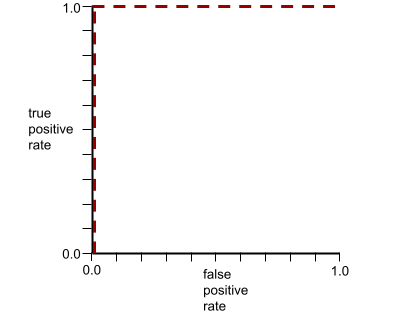
في المقابل، يوضح الرسم البياني التالي قيم الانحدار اللوجستي الأولية لنموذج سيئ لا يمكنه الفصل بين الفئات السلبية والفئات الإيجابية على الإطلاق:
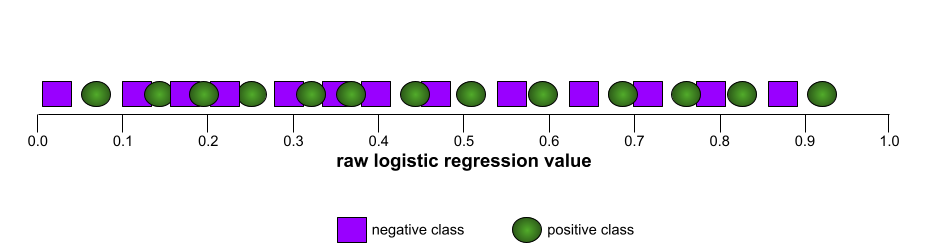
يبدو منحنى ROC لهذا النموذج على النحو التالي:
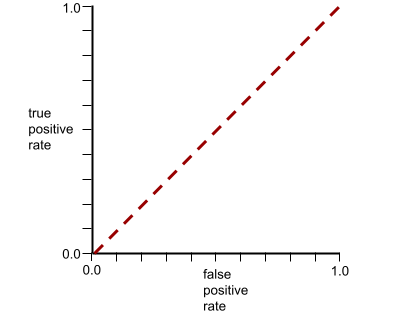
في الوقت نفسه، في العالم الحقيقي، تفصل معظم نماذج التصنيف الثنائي بين الفئات الإيجابية والسلبية إلى حد ما، ولكن ليس بشكل مثالي عادةً. لذا، يقع منحنى ROC النموذجي في مكان ما بين الحدّين الأقصى والأدنى:
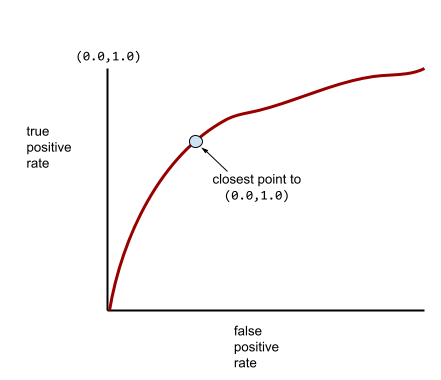
تحدّد النقطة الأقرب إلى (0.0,1.0) على منحنى ROC نظريًا عتبة التصنيف المثالية. ومع ذلك، تؤثر عدة مشاكل أخرى من العالم الحقيقي في اختيار الحد الأمثل للتصنيف. على سبيل المثال، قد تتسبّب النتائج السلبية الخاطئة في مشاكل أكثر من النتائج الإيجابية الخاطئة.
يلخّص مقياس عددي يُسمى AUC منحنى ROC في قيمة واحدة ذات فاصلة عائمة.
جذر الخطأ التربيعي المتوسّط (RMSE)
الجذر التربيعي لمتوسط الخطأ التربيعي
S
الدالّة الإسية
دالة رياضية "تضغط" قيمة إدخال في نطاق محدود، عادةً من 0 إلى 1 أو من -1 إلى +1. أي أنّه يمكنك تمرير أي رقم (اثنان أو مليون أو مليار سالب أو أي رقم آخر) إلى دالة Sigmoid وسيظل الناتج ضمن النطاق المحدود. يبدو الرسم البياني لدالة التنشيط السينية كما يلي:

تتعدّد استخدامات الدالة السينية في التعلّم الآلي، ومنها:
- تحويل الناتج الأوّلي لنموذج الانحدار اللوجستي أو نموذج الانحدار المتعدد الحدود إلى احتمالية
- العمل كدالة تنشيط في بعض الشبكات العصبية
softmax
دالة تحدّد الاحتمالات لكل فئة ممكنة في نموذج تصنيف متعدّد الفئات. ويجب أن يكون مجموع الاحتمالات 1.0. على سبيل المثال، يوضّح الجدول التالي كيف توزع دالة softmax الاحتمالات المختلفة:
| الصورة عبارة عن... | الاحتمالية |
|---|---|
| كلب | .85 |
| هرّ | .13 |
| حصان | .02 |
يُطلق على Softmax أيضًا اسم full softmax.
يختلف عن تحليل العينات المُحتملة.
لمزيد من المعلومات، يمكنك الاطّلاع على الشبكات العصبية: التصنيف المتعدد الفئات في "الدورة التدريبية المكثّفة حول تعلُّم الآلة".
خاصية متناثرة
ميزة تكون قيمها في الغالب صفرًا أو فارغة. على سبيل المثال، تكون الميزة التي تحتوي على قيمة واحدة تساوي 1 ومليون قيمة تساوي 0 متفرقة. في المقابل، تحتوي الميزة الكثيفة على قيم ليست صفرًا أو فارغة في الغالب.
في تعلُّم الآلة، يكون عدد كبير من الميزات ميزات متناثرة. السمات الفئوية هي عادةً سمات متناثرة. على سبيل المثال، من بين 300 نوع ممكن من الأشجار في غابة، قد يحدّد مثال واحد شجرة قيقب فقط. أو من بين ملايين الفيديوهات المحتملة في مكتبة فيديوهات، قد يحدّد مثال واحد فيلم "كازابلانكا" فقط.
في النموذج، يتم عادةً تمثيل الميزات المتفرقة باستخدام الترميز الأحادي. إذا كان التشفير الواحد الفعّال كبيرًا، يمكنك وضع طبقة تضمين فوق التشفير الواحد الفعّال لتحقيق كفاءة أكبر.
التمثيل المتناثر
تخزين مواضع العناصر غير الصفرية فقط في ميزة متفرقة
على سبيل المثال، لنفترض أنّ ميزة فئوية باسم species تحدّد 36 نوعًا من الأشجار في غابة معيّنة. افترض أيضًا أنّ كل مثال يحدّد نوعًا واحدًا فقط.
يمكنك استخدام متّجه الترميز الأحادي لتمثيل أنواع الأشجار في كل مثال.
سيتضمّن المتجه ذو الترميز الأحادي 1 واحدًا (لتمثيل نوع الشجرة المحدّد في هذا المثال) و35 0 (لتمثيل أنواع الأشجار الـ 35 غير المحدّدة في هذا المثال). لذا، قد يبدو التمثيل بترميز one-hot للرقم maple على النحو التالي:

بدلاً من ذلك، يمكن أن يحدّد التمثيل المتفرّق موضع النوع المعيّن. إذا كان maple في الموضع 24، سيكون التمثيل المتناثر
لـ maple على النحو التالي:
24
لاحظ أنّ التمثيل المتناثر أكثر إيجازًا من التمثيل بترميز "واحد ساخن".
لمزيد من المعلومات، راجِع استخدام البيانات الفئوية في "الدورة التدريبية المكثّفة حول تعلُّم الآلة".
متّجه متناثر
متجه تكون قيمه في الغالب أصفارًا راجِع أيضًا الميزة النادرة والندرة.
الخسارة التربيعية
مرادف الخسارةالتربيعية
ثابت
شيء يتم تنفيذه مرة واحدة بدلاً من تنفيذه بشكل مستمر المصطلحان ثابت وبلا إنترنت مترادفان. في ما يلي الاستخدامات الشائعة للبيانات الثابتة وغير المتصلة بالإنترنت في تعلّم الآلة:
- النموذج الثابت (أو النموذج بلا إنترنت) هو نموذج يتم تدريبه مرة واحدة ثم استخدامه لفترة من الوقت.
- التدريب الثابت (أو التدريب بلا اتصال بالإنترنت) هو عملية تدريب نموذج ثابت.
- الاستنتاج الثابت (أو الاستنتاج بلا إنترنت) هو عملية ينشئ فيها النموذج مجموعة من التوقّعات في كل مرة.
تتبايَن مع الصور الديناميكية.
الاستنتاج الثابت
مرادف الاستنتاج المؤخَّر
الثبات
سمة لا تتغيّر قيمها على مستوى سمة واحدة أو أكثر، وعادةً ما تكون هذه السمة هي الوقت. على سبيل المثال، تكون إحدى السمات ثابتة إذا كانت قيمها متشابهة تقريبًا في عامَي 2021 و2023.
في العالم الحقيقي، لا تتسم سوى عدد قليل جدًا من السمات بالثبات. حتى الميزات المرتبطة بالثبات (مثل مستوى سطح البحر) تتغير بمرور الوقت.
يختلف ذلك عن عدم الثبات.
النزول المتدرّج العشوائي (SGD)
خوارزمية انحدار التدرّج يكون فيها حجم الدفعة واحدًا. بعبارة أخرى، يتم تدريب SGD على مثال واحد يتم اختياره بشكل موحّد وعشوائي من مجموعة تدريب.
يمكنك الاطّلاع على الانحدار الخطي: المعلمات الفائقة في "دورة مكثّفة عن تعلُّم الآلة" للحصول على مزيد من المعلومات.
تعلُّم الآلة الموجَّه
تدريب نموذج من الميزات والتصنيفات المقابلة يمكن تشبيه تعلُّم الآلة الخاضع للإشراف بتعلُّم موضوع معيّن من خلال دراسة مجموعة من الأسئلة والإجابات المقابلة لها. بعد إتقان الربط بين الأسئلة والأجوبة، يمكن للطالب تقديم إجابات لأسئلة جديدة (لم يسبق له رؤيتها) حول الموضوع نفسه.
قارِن ذلك بتعلُّم الآلة غير الموجَّه.
يمكنك الاطّلاع على التعلم الخاضع للإشراف في دورة "مقدمة في تعلُّم الآلة" للحصول على مزيد من المعلومات.
خاصية مصطنعة
ميزة غير متوفّرة بين الميزات المُدخَلة، ولكن تم تجميعها من ميزة واحدة أو أكثر من الميزات المُدخَلة تشمل طرق إنشاء الميزات الاصطناعية ما يلي:
- تصنيف ميزة مستمرة في نطاقات.
- إنشاء ميزة متقاطعة
- ضرب (أو قسمة) قيمة ميزة واحدة على قيم ميزات أخرى أو على نفسها على سبيل المثال، إذا كانت
aوbمن سمات الإدخال، ستكون الأمثلة التالية من السمات المصطنعة:- ab
- a2
- تطبيق دالة متسامية على قيمة سمة على سبيل المثال، إذا كانت
cإحدى سمات الإدخال، تكون الأمثلة التالية من السمات الاصطناعية:- sin(c)
- ln(c)
لا تُعتبر الميزات التي يتم إنشاؤها من خلال التسوية أو التحجيم وحدها ميزات اصطناعية.
T
الخسارة في مجموعة الاختبار
مقياس يمثّل الخسارة التي يتكبّدها النموذج مقارنةً بمجموعة الاختبار عند إنشاء نموذج، تحاول عادةً تقليل خسارة الاختبار. ويرجع ذلك إلى أنّ انخفاض مقياس القصور في مجموعة الاختبار هو إشارة جودة أقوى من انخفاض مقياس القصور في مجموعة التدريب أو انخفاض مقياس القصور في مجموعة التحقّق.
يشير الفرق الكبير بين خسارة الاختبار وخسارة التدريب أو خسارة التحقّق أحيانًا إلى ضرورة زيادة معدّل التسوية.
التدريب
تشير إلى عملية تحديد المَعلمات المثالية (الأوزان والانحيازات) التي يتألف منها النموذج. أثناء التدريب، يقرأ النظام أمثلة ويعدّل المَعلمات تدريجيًا. يتم استخدام كل مثال في التدريب من بضع مرات إلى مليارات المرات.
يمكنك الاطّلاع على التعلم الخاضع للإشراف في دورة "مقدمة في تعلُّم الآلة" للحصول على مزيد من المعلومات.
فقدان التدريب
مقياس يمثّل الخسارة التي يتكبّدها النموذج أثناء عملية تدريب معيّنة. على سبيل المثال، لنفترض أنّ دالة الخسارة هي متوسط الخطأ التربيعي. على سبيل المثال، قد يكون فقدان التدريب (متوسط الخطأ التربيعي) في التكرار العاشر هو 2.2، بينما يكون فقدان التدريب في التكرار المئة هو 1.9.
يعرض مخطّط الخسارة الخسارة أثناء التدريب مقابل عدد التكرارات. تقدّم منحنى الخسارة التلميحات التالية حول التدريب:
- يشير الميل الهبوطي إلى أنّ النموذج يتحسّن.
- يشير الميل التصاعدي إلى أنّ النموذج يزداد سوءًا.
- يشير الميل المسطّح إلى أنّ النموذج قد بلغ حالة التقارب.
على سبيل المثال، يوضّح منحنى الخسارة المثالي إلى حد ما التالي ما يلي:
- ميل حادّ نحو الأسفل خلال التكرارات الأولية، ما يشير إلى تحسُّن سريع في النموذج
- ميلان تدريجي نحو التسطّح (ولكنّه لا يزال نحو الأسفل) إلى أن يقترب من نهاية التدريب، ما يشير إلى تحسّن مستمر في النموذج بوتيرة أبطأ بعض الشيء من الوتيرة التي كانت سائدة خلال التكرارات الأولية
- ميل مستوٍ في نهاية التدريب، ما يشير إلى التقارب
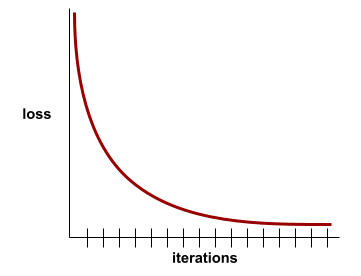
على الرغم من أهمية فقدان التدريب، يمكنك أيضًا الاطّلاع على التعميم.
اختلاف بين بيانات التدريب وبيانات العرض
الفرق بين أداء النموذج أثناء التدريب وأداء النموذج نفسه أثناء العرض
مجموعة التدريب
مجموعة فرعية من مجموعة البيانات المستخدَمة لتدريب نموذج
عادةً، يتم تقسيم الأمثلة في مجموعة البيانات إلى ثلاث مجموعات فرعية مميزة كما يلي:
- مجموعة تدريب
- مجموعة التحقّق
- مجموعة اختبار
يُفضّل أن ينتمي كل مثال في مجموعة البيانات إلى مجموعة فرعية واحدة فقط من المجموعات الفرعية السابقة. على سبيل المثال، يجب ألا ينتمي مثال واحد إلى كل من مجموعة التدريب ومجموعة التحقّق.
اطّلِع على مجموعات البيانات: تقسيم مجموعة البيانات الأصلية في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
سالب صحيح
مثال يوضّح أنّ النموذج توقّع الفئة السلبية بشكل صحيح. على سبيل المثال، يستنتج النموذج أنّ رسالة إلكترونية معيّنة ليست غير مرغوب فيها، وأنّ هذه الرسالة الإلكترونية ليست غير مرغوب فيها بالفعل.
موجب صحيح (TP)
مثال يقدّم فيه النموذج توقّعًا صحيحًا للفئة الإيجابية. على سبيل المثال، يستنتج النموذج أنّ رسالة إلكترونية معيّنة هي رسالة غير مرغوب فيها، وتكون هذه الرسالة الإلكترونية في الواقع رسالة غير مرغوب فيها.
معدّل الموجب الصحيح (TPR)
مرادف لكلمة استدعاء والمقصود:
معدل الموجب الصحيح هو المحور الصادي في منحنى ROC.
U
فرط التعميم
إنتاج نموذج بقدرة توقّعية ضعيفة لأنّ النموذج لم يستوعب بشكل كامل مدى تعقيد بيانات التدريب يمكن أن تؤدي مشاكل عديدة إلى حدوث نقص في الملاءمة، بما في ذلك:
- التدريب على مجموعة خاطئة من الميزات
- التدريب لعدد قليل جدًا من الحقبات أو بمعدّل تعلّم منخفض جدًا
- التدريب بمعدّل تسوية مرتفع جدًا
- توفير عدد قليل جدًا من الطبقات المخفية في شبكة عصبونية عميقة
يمكنك الاطّلاع على الإفراط في التخصيص في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
مثال غير مصنّف
مثال يتضمّن ميزات ولكن بدون تصنيف على سبيل المثال، يعرض الجدول التالي ثلاثة أمثلة غير مصنَّفة من نموذج لتقييم المنازل، ويتضمّن كل مثال ثلاث سمات ولكن بدون قيمة للمنزل:
| عدد غرف النوم | عدد الحمّامات | عمر المنزل |
|---|---|---|
| 3 | 2 | 15 |
| 2 | 1 | 72 |
| 4 | 2 | 34 |
في تعلُّم الآلة الموجَّه، يتم تدريب النماذج على أمثلة مصنَّفة، ويتم إجراء توقعات على أمثلة غير مصنَّفة.
في التعلّم شبه الموجَّه وغير الموجَّه، يتم استخدام أمثلة غير مصنَّفة أثناء التدريب.
قارِن المثال غير المصنّف بالمثال المصنّف.
تعلُّم الآلة غير الموجَّه
تدريب نموذج للعثور على أنماط في مجموعة بيانات، وعادةً ما تكون مجموعة بيانات غير مصنَّفة
إنّ الاستخدام الأكثر شيوعًا للتعلّم الآلي غير الموجَّه هو تجميع البيانات في مجموعات من الأمثلة المتشابهة. على سبيل المثال، يمكن لخوارزمية تعلّم آلي غير مراقبة تجميع الأغاني استنادًا إلى خصائص مختلفة للموسيقى. ويمكن أن تصبح المجموعات الناتجة مدخلاً لخوارزميات أخرى لتعلُّم الآلة (على سبيل المثال، لخدمة اقتراحات موسيقية). يمكن أن يساعد التجميع العنقودي عندما تكون التصنيفات المفيدة نادرة أو غير متوفّرة. على سبيل المثال، في مجالات مثل مكافحة إساءة الاستخدام والاحتيال، يمكن أن تساعد المجموعات البشر في فهم البيانات بشكل أفضل.
يختلف عن تعلُّم الآلة الموجَّه.
يمكنك الاطّلاع على ما هي تكنولوجيا تعلُّم الآلة؟ في دورة "مقدمة إلى تعلُّم الآلة" التدريبية للحصول على مزيد من المعلومات.
V
الإثبات
التقييم الأوّلي لجودة النموذج تتحقّق عملية التحقّق من صحة البيانات من جودة توقّعات النموذج من خلال مقارنتها بمجموعة التحقّق من صحة البيانات.
بما أنّ مجموعة التحقّق تختلف عن مجموعة التدريب، يساعد التحقّق في الحماية من التطابق الزائد.
يمكنك اعتبار تقييم النموذج استنادًا إلى مجموعة التحقّق بمثابة الجولة الأولى من الاختبار، وتقييم النموذج استنادًا إلى مجموعة الاختبار بمثابة الجولة الثانية من الاختبار.
فقدان التحقّق من الصحة
مقياس يمثّل الخسارة التي يتكبّدها النموذج على مجموعة التحقّق خلال تكرار معيّن من التدريب.
يمكنك أيضًا الاطّلاع على منحنى التعميم.
مجموعة التحقّق
مجموعة فرعية من مجموعة البيانات التي تجري تقييمًا أوليًا مقارنةً بنموذج تم تدريبه. عادةً، يتم تقييم النموذج المدرَّب استنادًا إلى مجموعة التحقّق عدة مرات قبل تقييم النموذج استنادًا إلى مجموعة الاختبار.
عادةً، يتم تقسيم الأمثلة في مجموعة البيانات إلى المجموعات الفرعية الثلاث التالية المميّزة:
- مجموعة تدريب
- مجموعة التحقّق
- مجموعة اختبار
يُفضّل أن ينتمي كل مثال في مجموعة البيانات إلى مجموعة فرعية واحدة فقط من المجموعات الفرعية السابقة. على سبيل المثال، يجب ألا ينتمي مثال واحد إلى كل من مجموعة التدريب ومجموعة التحقّق.
اطّلِع على مجموعات البيانات: تقسيم مجموعة البيانات الأصلية في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
واط
الوزن
قيمة يضربها النموذج في قيمة أخرى. التدريب هو عملية تحديد الأوزان المثالية للنموذج، بينما الاستدلال هو عملية استخدام تلك الأوزان التي تم تعلّمها لإجراء التوقعات.
يمكنك الاطّلاع على الانحدار الخطي في "دورة مكثّفة عن تعلّم الآلة" للحصول على مزيد من المعلومات.
المجموع الموزون
مجموع كل قيم الإدخال ذات الصلة مضروبًا في الأوزان المقابلة لها. على سبيل المثال، لنفترض أنّ المدخلات ذات الصلة تتألف مما يلي:
| قيمة الإدخال | وزن الإدخال |
| 2 | -1.3 |
| -1 | 0.6 |
| 3 | 0.4 |
وبالتالي، يكون المجموع المرجّح كما يلي:
weighted sum = (2)(-1.3) + (-1)(0.6) + (3)(0.4) = -2.0
المجموع المرجّح هو وسيطة الإدخال إلى دالة التنشيط.
Z
التسوية باستخدام درجة Z
التحجيم هو أسلوب يستبدل قيمة سمة أولية بقيمة نقطة عائمة تمثّل عدد الانحرافات المعيارية عن متوسط تلك السمة. على سبيل المثال، لنفترض أنّ هناك ميزة متوسطها 800 وانحرافها المعياري 100. يوضّح الجدول التالي كيف يمكن أن يؤدي التوحيد القياسي لنتيجة Z إلى ربط القيمة الأولية بنتيجة Z:
| قيمة أساسية | الدرجة المعيارية |
|---|---|
| 800 | 0 |
| 950 | +1.5 |
| 575 | -2.25 |
بعد ذلك، يتم تدريب نموذج تعلُّم الآلة على قيم Z الخاصة بهذه السمة بدلاً من القيم الأولية.
يمكنك الاطّلاع على البيانات الرقمية: التسوية في "الدورة التدريبية المكثّفة حول تعلُّم الآلة" للحصول على مزيد من المعلومات.