Ta strona zawiera terminy z glosariusza dotyczące lasów decyzyjnych. Aby wyświetlić wszystkie terminy z glosariusza, kliknij tutaj.
A
próbkowanie atrybutów,
Taktyka trenowania lasu decyzyjnego, w której każde drzewo decyzyjne podczas uczenia się warunku bierze pod uwagę tylko losowy podzbiór możliwych cech. Zwykle w przypadku każdego węzła próbkowany jest inny podzbiór cech. Z kolei podczas trenowania drzewa decyzyjnego bez próbkowania atrybutów w przypadku każdego węzła brane są pod uwagę wszystkie możliwe cechy.
warunek wyrównany do osi
W drzewie decyzyjnym warunek
obejmujący tylko 1 obiekt. Jeśli na przykład area jest cechą, to warunek wyrównany do osi wygląda tak:
area > 200
Kontrast z warunkiem ukośnym.
B
bagging
Metoda trenowania zespołu, w którym każdy model składowy jest trenowany na losowym podzbiorze przykładów treningowych próbkowanych z powtórzeniami. Na przykład las losowy to zbiór drzew decyzyjnych wytrenowanych za pomocą metody baggingu.
Termin bagging to skrót od bootstrap aggregating.
Więcej informacji znajdziesz w sekcji Las losowy w kursie Decision Forests.
warunek binarny
W drzewie decyzyjnym warunek, który ma tylko 2 możliwe wyniki, zwykle tak lub nie. Na przykład warunek binarny to:
temperature >= 100
Porównaj z warunkiem niebinarnym.
Więcej informacji znajdziesz w sekcji Rodzaje warunków w kursie Decision Forests.
C
warunek
W drzewie decyzyjnym każdy węzeł, który przeprowadza test. Na przykład to drzewo decyzyjne zawiera 2 warunki:
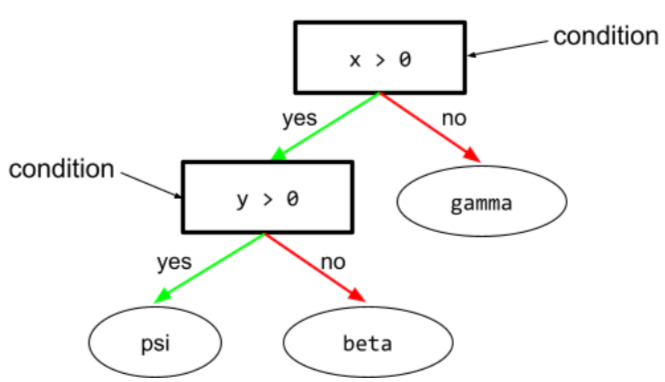
Warunek jest też nazywany podziałem lub testem.
Warunek kontrastu z leaf.
Zobacz także:
Więcej informacji znajdziesz w sekcji Rodzaje warunków w kursie Decision Forests.
D
las decyzyjny,
Model utworzony z wielu drzew decyzyjnych. Las decyzyjny tworzy prognozę, agregując prognozy drzew decyzyjnych. Popularne rodzaje lasów decyzyjnych to lasy losowe i drzewa wzmocnione gradientowo.
Więcej informacji znajdziesz w sekcji Lasy decyzyjne w kursie Lasy decyzyjne.
drzewo decyzyjne,
Nadzorowany model systemów uczących się składający się z zestawu warunków i węzłów końcowych uporządkowanych hierarchicznie. Oto przykład drzewa decyzyjnego:
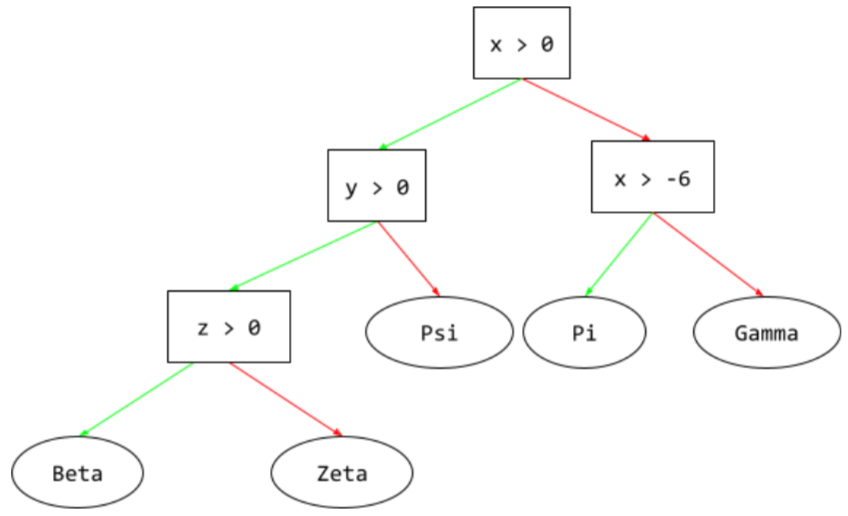
E
entropia
W teorii informacji jest to opis tego, jak nieprzewidywalny jest rozkład prawdopodobieństwa. Entropia jest też definiowana jako ilość informacji zawartych w każdym przykładzie. Rozkład ma najwyższą możliwą entropię, gdy wszystkie wartości zmiennej losowej są jednakowo prawdopodobne.
Entropia zbioru z 2 możliwymi wartościami „0” i „1” (np. etykietami w problemie klasyfikacji binarnej) ma następujący wzór:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
gdzie:
- H to entropia.
- p to ułamek przykładów „1”.
- q to ułamek przykładów „0”. Pamiętaj, że q = (1 – p).
- log to zwykle log2. W tym przypadku jednostką entropii jest bit.
Załóżmy na przykład, że:
- 100 przykładów zawiera wartość „1”
- 300 przykładów zawiera wartość „0”
Wartość entropii wynosi więc:
- p = 0,25
- q = 0,75
- H = (-0,25)log2(0,25) - (0,75)log2(0,75) = 0,81 bita na przykład
Zbiór, który jest doskonale zrównoważony (np.200 zer i 200 jedynek), ma entropię 1,0 bita na przykład. W miarę jak zbiór staje się bardziej niezrównoważony, jego entropia zbliża się do 0,0.
W drzewach decyzyjnych entropia pomaga formułować przyrost informacji, aby rozdzielacz mógł wybierać warunki podczas tworzenia drzewa decyzyjnego klasyfikacji.
Porównaj entropię z:
- zanieczyszczenie Giniego
- funkcja straty entropii krzyżowej,
Entropia jest często nazywana entropią Shannona.
Więcej informacji znajdziesz w sekcji Exact splitter for binary classification with numerical features (Dokładny rozdzielacz do klasyfikacji binarnej z cechami numerycznymi) w kursie Decision Forests.
P
znaczenie cech,
Synonim terminu znaczenie zmiennych.
G
zanieczyszczenie Giniego,
Dane podobne do entropii. Rozdzielacze używają wartości pochodzących z nieczystości Giniego lub entropii do tworzenia warunków klasyfikacji drzew decyzyjnych. Przyrost informacji jest obliczany na podstawie entropii. Nie ma powszechnie akceptowanego odpowiednika terminu dla danych pochodnych z nieczystości Giniego, ale te nienazwane dane są równie ważne jak przyrost informacji.
Zanieczyszczenie Giniego jest też nazywane wskaźnikiem Giniego lub po prostu gini.
wzmocnione gradientowo drzewa decyzyjne (GBT),
Rodzaj lasu decyzyjnego, w którym:
- Trenowanie opiera się na wzmocnieniu gradientowym.
- Słabym modelem jest drzewo decyzyjne.
Więcej informacji znajdziesz w lekcji o drzewach decyzyjnych z wzmocnieniem gradientowym w kursie Decision Forests.
wzmocnienie gradientowe,
Algorytm trenowania, w którym słabe modele są trenowane w celu iteracyjnego poprawiania jakości (zmniejszania straty) silnego modelu. Przykładem słabego modelu może być model liniowy lub mały model drzewa decyzyjnego. Silny model staje się sumą wszystkich wcześniej wytrenowanych słabych modeli.
W najprostszej formie wzmacniania gradientowego w każdej iteracji trenowany jest słaby model, który ma przewidywać gradient funkcji straty silnego modelu. Następnie dane wyjściowe modelu o wysokiej skuteczności są aktualizowane przez odjęcie przewidywanego gradientu, podobnie jak w przypadku metody gradientu prostego.
gdzie:
- $F_{0}$ to model początkowy.
- $F_{i+1}$ to kolejny silny model.
- $F_{i}$ to bieżący model o wysokiej skuteczności.
- $\xi$ to wartość z zakresu od 0,0 do 1,0, zwana kurczeniem, która jest analogiczna do szybkości uczenia w metodzie spadku gradientowego.
- $f_{i}$ to słaby model wytrenowany do przewidywania gradientu funkcji straty $F_{i}$.
Nowoczesne odmiany wzmacniania gradientowego uwzględniają też w obliczeniach drugą pochodną (hesjan) funkcji straty.
Drzewa decyzyjne są często używane jako słabe modele w metodzie gradient boosting. Zobacz drzewa decyzyjne z wzmocnieniem gradientowym.
I
ścieżka wnioskowania
W drzewie decyzyjnym podczas wnioskowania przykład przechodzi od korzenia do innych warunków, kończąc na liściu. Na przykład na poniższym schemacie decyzyjnym grubsze strzałki pokazują ścieżkę wnioskowania dla przykładu o tych wartościach cech:
- x = 7
- y = 12
- z = -3
Ścieżka wnioskowania na poniższej ilustracji przechodzi przez 3 warunki, zanim dotrze do węzła końcowego (Zeta).
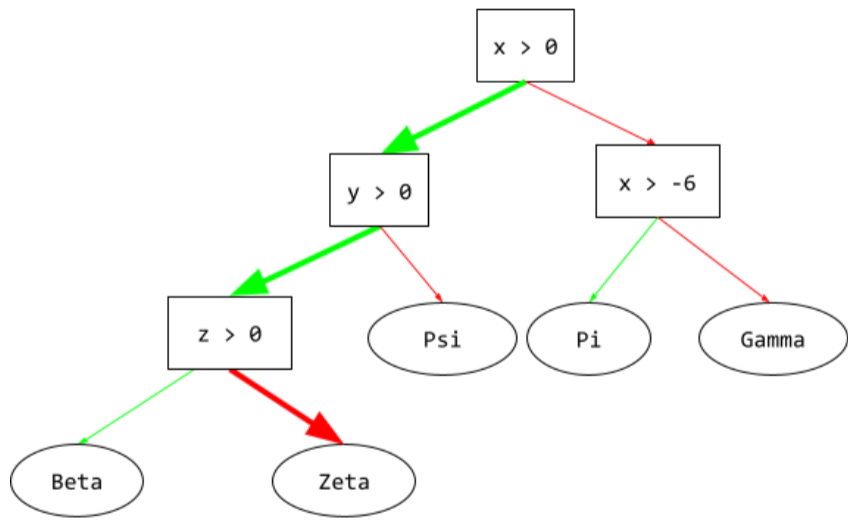
Trzy grube strzałki pokazują ścieżkę wnioskowania.
Więcej informacji znajdziesz w sekcji Drzewa decyzyjne w kursie Lasy decyzyjne.
przyrost informacji
W lasach decyzyjnych różnica między entropią węzła a ważoną (według liczby przykładów) sumą entropii jego węzłów podrzędnych. Entropia węzła to entropia przykładów w tym węźle.
Rozważmy na przykład te wartości entropii:
- entropia węzła nadrzędnego = 0,6
- entropia jednego węzła podrzędnego z 16 odpowiednimi przykładami = 0,2.
- entropia innego węzła podrzędnego z 24 odpowiednimi przykładami = 0,1
40% przykładów znajduje się w jednym węźle podrzędnym, a 60% – w drugim. Dlatego:
- ważona suma entropii węzłów podrzędnych = (0,4 * 0,2) + (0,6 * 0,1) = 0,14
Zatem przyrost informacji wynosi:
- przyrost informacji = entropia węzła nadrzędnego – ważona suma entropii węzłów podrzędnych
- przyrost informacji = 0,6 – 0,14 = 0,46
Większość rozdzielaczy dąży do tworzenia warunków, które maksymalizują przyrost informacji.
warunek w zbiorze
W drzewie decyzyjnym warunek, który sprawdza, czy w zbiorze elementów znajduje się jeden element. Na przykład ten warunek należy do zbioru:
house-style in [tudor, colonial, cape]
Podczas wnioskowania, jeśli wartość stylu domu feature wynosi tudor, colonial lub cape, warunek ten jest spełniony. Jeśli wartość funkcji stylu domu jest inna (np. ranch), warunek przyjmuje wartość „Nie”.
Warunki zbioru zwykle prowadzą do bardziej wydajnych drzew decyzyjnych niż warunki, które testują cechy zakodowane metodą 1-z-N.
L
liść
Dowolny punkt końcowy w drzewie decyzyjnym. W przeciwieństwie do warunku węzeł końcowy nie przeprowadza testu. Liść jest raczej możliwą prognozą. Liść jest też węzłem końcowym ścieżki wnioskowania.
Na przykład to drzewo decyzyjne zawiera 3 liście:
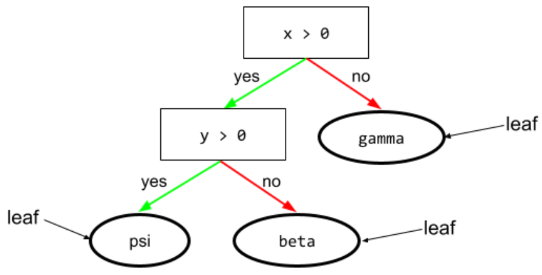
Więcej informacji znajdziesz w sekcji Drzewa decyzyjne w kursie Lasy decyzyjne.
N
węzeł (drzewo decyzyjne)
W drzewie decyzyjnym dowolny warunek lub węzeł.

Więcej informacji znajdziesz w schematach decyzyjnych w kursie Decision Forests.
warunek niebinarny
Warunek zawierający więcej niż 2 możliwe wyniki. Na przykład poniższy warunek niebinarny ma 3 możliwe wyniki:
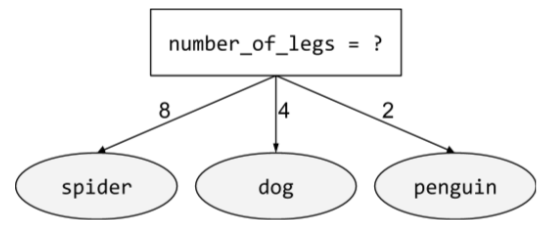
Więcej informacji znajdziesz w sekcji Rodzaje warunków w kursie Decision Forests.
O
warunek ukośny
W drzewie decyzyjnym warunek, który obejmuje więcej niż 1 cechę. Jeśli np. wysokość i szerokość są cechami, warunek ukośny może wyglądać tak:
height > width
Porównaj z warunkiem wyrównanym do osi.
Więcej informacji znajdziesz w sekcji Rodzaje warunków w kursie Decision Forests.
ocena poza próbą (OOB)
Mechanizm oceny jakości lasu decyzyjnego przez testowanie każdego drzewa decyzyjnego na przykładach, które nie były używane podczas trenowania tego drzewa decyzyjnego. Na przykład na poniższym diagramie widać, że system trenuje każde drzewo decyzyjne na około 2/3 przykładów, a następnie ocenia je na pozostałej 1/3 przykładów.
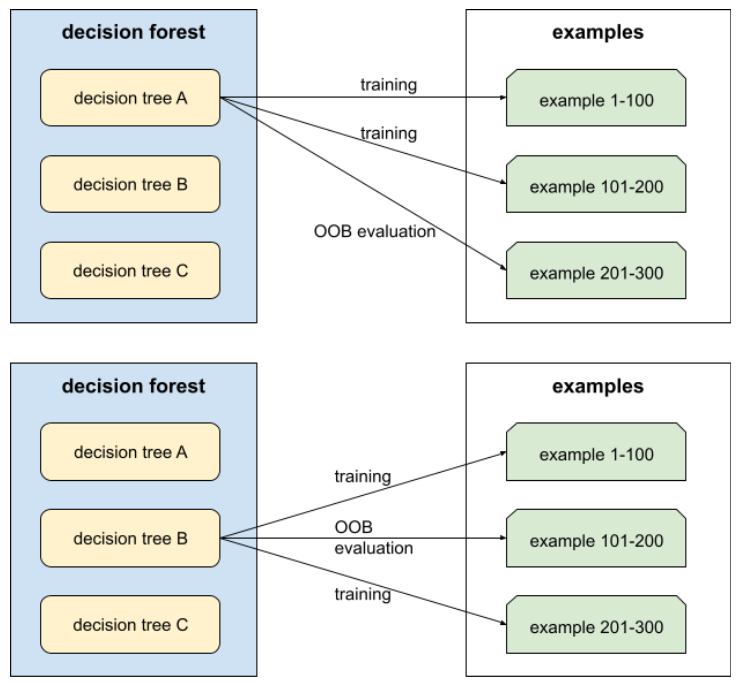
Ocena poza próbą jest wydajnym obliczeniowo i konserwatywnym przybliżeniem mechanizmu walidacji krzyżowej. W przypadku weryfikacji krzyżowej trenowany jest jeden model w każdej rundzie weryfikacji krzyżowej (np. w 10-krotnej weryfikacji krzyżowej trenowanych jest 10 modeli). W przypadku oceny OOB trenowany jest jeden model. Ponieważ bagging podczas trenowania każdego drzewa pomija część danych, ocena OOB może wykorzystać te dane do przybliżonego przeprowadzenia walidacji krzyżowej.
Więcej informacji znajdziesz w sekcji Ocena poza próbą w kursie Decision Forests.
P
permutacyjna ważność zmiennych
Rodzaj znaczenia zmiennej, który ocenia wzrost błędu prognozy modelu po przestawieniu wartości cechy. Permutacyjna ważność zmiennych to niezależny od modelu wskaźnik.
R
las losowy,
Zespół drzew decyzyjnych, w którym każde drzewo decyzyjne jest trenowane z użyciem określonego losowego szumu, np. baggingu.
Lasy losowe to rodzaj lasu decyzyjnego.
Więcej informacji znajdziesz w sekcji Random Forest w kursie Decision Forests.
poziom główny
Węzeł początkowy (pierwszy warunek) w drzewie decyzyjnym. Zgodnie z konwencją korzeń umieszcza się u góry drzewa decyzyjnego. Na przykład:
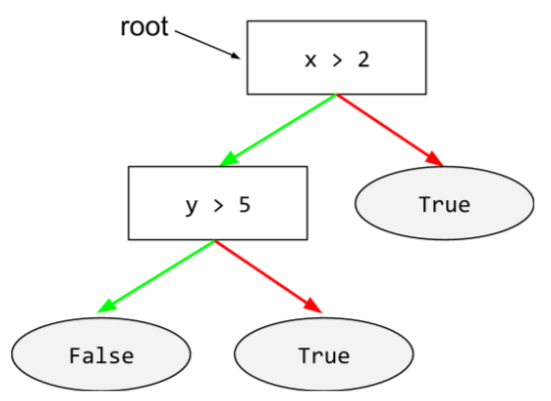
S
próbkowanie ze zwracaniem,
Metoda wybierania elementów ze zbioru kandydatów, w której ten sam element może być wybierany wielokrotnie. Określenie „z powtórzeniami” oznacza, że po każdym wyborze wybrany element jest zwracany do puli kandydatów. Metoda odwrotna, czyli próbkowanie bez zwracania, oznacza, że element kandydujący może zostać wybrany tylko raz.
Rozważmy na przykład ten zbiór owoców:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Załóżmy, że system losowo wybiera fig jako pierwszy element.
Jeśli używasz próbkowania ze zwracaniem, system wybiera drugi element z tego zbioru:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Tak, to ten sam zestaw co wcześniej, więc system może ponownie wybrać fig.
Jeśli używasz próbkowania bez zwracania, po wybraniu próbki nie można jej ponownie wybrać. Jeśli na przykład system losowo wybierze fig jako pierwszą próbkę, nie może jej ponownie wybrać.fig Dlatego system wybiera drugą próbkę z tego (mniejszego) zbioru:
fruit = {kiwi, apple, pear, cherry, lime, mango}kurczenie się,
Hiperparametr w wzmocnieniu gradientowym, który kontroluje przetrenowanie. Kurczenie się w przypadku wzmocnienia gradientowego jest analogiczne do tempa uczenia się w metodzie gradientu prostego. Skurcz to liczba dziesiętna z zakresu od 0,0 do 1,0. Niższa wartość kurczenia zmniejsza przeuczenie bardziej niż wyższa.
podziel
W drzewie decyzyjnym to inna nazwa warunku.
rozdzielacz,
Podczas trenowania drzewa decyzyjnego procedura (i algorytm) odpowiedzialna za znajdowanie najlepszego warunku w każdym węźle.
T
test
W drzewie decyzyjnym to inna nazwa warunku.
próg (w przypadku drzew decyzyjnych);
W warunku wyrównanym do osi wartość, z którą porównywana jest cecha. Na przykład w tym warunku wartością progową jest 75:
grade >= 75
Więcej informacji znajdziesz w dokładnym rozdzielaczu do klasyfikacji binarnej z cechami numerycznymi w kursie Decision Forests.
V
ważność zmiennych,
Zestaw wyników, który wskazuje względne znaczenie każdej cechy dla modelu.
Weźmy na przykład drzewo decyzyjne, które szacuje ceny domów. Załóżmy, że to drzewo decyzyjne korzysta z 3 cech: rozmiaru, wieku i stylu. Jeśli zestaw ważności zmiennych dla 3 cech wynosi {rozmiar=5,8, wiek=2,5, styl=4,7}, to rozmiar jest ważniejszy dla drzewa decyzyjnego niż wiek czy styl.
Istnieją różne rodzaje danych o znaczeniu zmiennych, które mogą dostarczać ekspertom ds. uczenia maszynowego informacji o różnych aspektach modeli.
W
mądrość tłumu
Teoria, że uśrednianie opinii lub szacunków dużej grupy osób („tłumu”) często daje zaskakująco dobre wyniki. Weźmy na przykład grę, w której uczestnicy zgadują liczbę żelków w dużym słoiku. Chociaż większość pojedynczych odpowiedzi będzie niedokładna, średnia wszystkich odpowiedzi jest zaskakująco bliska rzeczywistej liczbie cukierków w słoiku.
Modele zespołowe to odpowiednik w oprogramowaniu koncepcji mądrości tłumu. Nawet jeśli poszczególne modele generują bardzo niedokładne prognozy, uśrednianie prognoz wielu modeli często daje zaskakująco dobre wyniki. Na przykład pojedyncze drzewo decyzyjne może dawać słabe prognozy, ale las decyzyjny często daje bardzo dobre prognozy.