Questa pagina contiene i termini del glossario di Decision Forests. Per tutti i termini del glossario, fai clic qui.
A
campionamento degli attributi
Una tattica per l'addestramento di una foresta decisionale in cui ogni albero decisionale considera solo un sottoinsieme casuale di possibili caratteristiche durante l'apprendimento della condizione. In genere, per ogni nodo viene campionato un sottoinsieme diverso di funzionalità. Al contrario, quando si addestra un albero decisionale senza campionamento degli attributi, vengono prese in considerazione tutte le funzionalità possibili per ogni nodo.
condizione allineata all'asse
In un albero decisionale, una condizione
che coinvolge una sola caratteristica. Ad esempio, se area
è una funzionalità, la seguente è una condizione allineata all'asse:
area > 200
Contrasto con la condizione obliqua.
B
bagging
Un metodo per addestrare un ensemble in cui ogni modello costituente viene addestrato su un sottoinsieme casuale di esempi di addestramento campionati con reinserimento. Ad esempio, una foresta casuale è un insieme di alberi decisionali addestrati con il bagging.
Il termine bagging è l'abbreviazione di bootstrap aggregating.
Per ulteriori informazioni, consulta la sezione Foreste casuali del corso Decision Forests.
condizione binaria
In un albero decisionale, una condizione che ha solo due possibili risultati, in genere sì o no. Ad esempio, la seguente è una condizione binaria:
temperature >= 100
Contrasto con la condizione non binaria.
Per ulteriori informazioni, consulta la sezione Tipi di condizioni del corso Decision Forests.
C
condizione
In un albero decisionale, qualsiasi nodo che esegue un test. Ad esempio, il seguente albero decisionale contiene due condizioni:
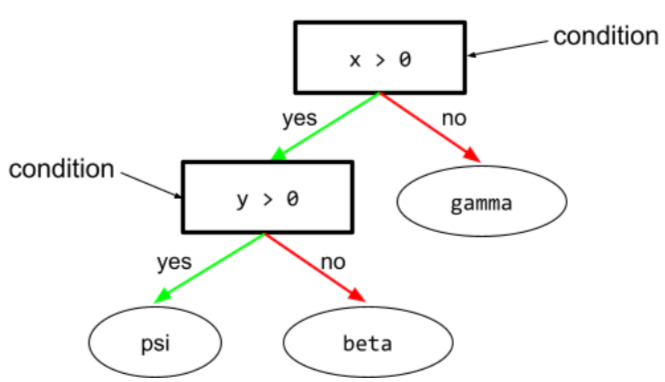
Una condizione è chiamata anche divisione o test.
Condizione di contrasto con foglia.
Vedi anche:
Per ulteriori informazioni, consulta la sezione Tipi di condizioni del corso Decision Forests.
D
foresta di alberi decisionali
Un modello creato da più alberi decisionali. Una foresta decisionale fa una previsione aggregando le previsioni dei suoi alberi decisionali. I tipi più comuni di foreste decisionali includono foreste casuali e alberi potenziati dal gradiente.
Per ulteriori informazioni, consulta la sezione Foreste decisionali del corso sulle foreste decisionali.
albero decisionale
Un modello di apprendimento supervisionato composto da un insieme di condizioni e foglie organizzate gerarchicamente. Ad esempio, di seguito è riportata una struttura decisionale:
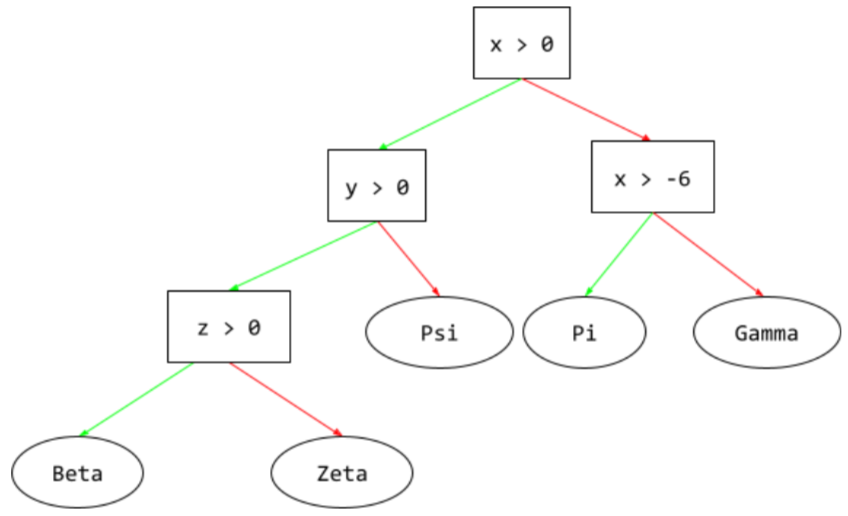
E
entropia
Nella teoria dell'informazione, una descrizione di quanto sia imprevedibile una distribuzione di probabilità. In alternativa, l'entropia è anche definita come la quantità di informazioni contenute in ogni esempio. Una distribuzione ha l'entropia più alta possibile quando tutti i valori di una variabile casuale sono ugualmente probabili.
L'entropia di un insieme con due possibili valori "0" e "1" (ad esempio, le etichette in un problema di classificazione binaria) ha la seguente formula:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
dove:
- H è l'entropia.
- p è la frazione di esempi "1".
- q è la frazione di esempi "0". Tieni presente che q = (1 - p)
- log è generalmente log2. In questo caso, l'unità di entropia è un bit.
Ad esempio, supponiamo quanto segue:
- 100 esempi contengono il valore "1"
- 300 esempi contengono il valore "0"
Pertanto, il valore di entropia è:
- p = 0,25
- q = 0,75
- H = (-0,25)log2(0,25) - (0,75)log2(0,75) = 0,81 bit per esempio
Un insieme perfettamente bilanciato (ad esempio, 200 "0" e 200 "1") avrebbe un'entropia di 1 bit per esempio. Man mano che un insieme diventa più sbilanciato, la sua entropia tende a 0.
Negli alberi decisionali, l'entropia aiuta a formulare il guadagno di informazioni per aiutare lo splitter a selezionare le condizioni durante la crescita di un albero decisionale di classificazione.
Confronta l'entropia con:
- Impurità di Gini
- Funzione di perdita entropia incrociata
L'entropia viene spesso chiamata entropia di Shannon.
Per saperne di più, consulta Splitter esatto per la classificazione binaria con funzionalità numeriche nel corso Decision Forests.
V
importanza delle caratteristiche
Sinonimo di importanza delle variabili.
G
Impurità di Gini
Una metrica simile all'entropia. Gli splitter utilizzano valori derivati dall'impurità di Gini o dall'entropia per comporre condizioni per gli alberi decisionali. L'information gain deriva dall'entropia. Non esiste un termine equivalente accettato universalmente per la metrica derivata dall'impurità di Gini; tuttavia, questa metrica senza nome è importante quanto l'information gain.
L'impurità di Gini è chiamata anche indice di Gini o semplicemente Gini.
alberi (decisionali) con boosting del gradiente (GBT)
Un tipo di foresta decisionale in cui:
- L'addestramento si basa sul gradient boosting.
- Il modello debole è un albero decisionale.
Per ulteriori informazioni, consulta la sezione Gradient Boosted Decision Trees del corso Decision Forests.
gradient boosting
Un algoritmo di addestramento in cui i modelli deboli vengono addestrati per migliorare iterativamente la qualità (ridurre la perdita) di un modello forte. Ad esempio, un modello debole potrebbe essere un modello lineare o un piccolo albero decisionale. Il modello forte diventa la somma di tutti i modelli deboli addestrati in precedenza.
Nella forma più semplice di gradient boosting, a ogni iterazione viene addestrato un modello debole per prevedere il gradiente di perdita del modello forte. Quindi, l'output del modello robusto viene aggiornato sottraendo il gradiente previsto, in modo simile alla discesa del gradiente.
dove:
- $F_{0}$ è il modello di partenza.
- $F_{i+1}$ è il modello forte successivo.
- $F_{i}$ è il modello forte attuale.
- $\xi$ è un valore compreso tra 0,0 e 1,0 chiamato restringimento, che è analogo al tasso di apprendimento nella discesa del gradiente.
- $f_{i}$ è il modello debole addestrato per prevedere il gradiente di perdita di $F_{i}$.
Le varianti moderne del gradient boosting includono anche la derivata seconda (Hessiana) della perdita nel calcolo.
Gli alberi decisionali vengono comunemente utilizzati come modelli deboli nel gradient boosting. Vedi alberi (decisionali) con potenziamento del gradiente.
I
percorso di inferenza
In un albero decisionale, durante l'inferenza, il percorso che un particolare esempio segue dalla radice ad altre condizioni, terminando con una foglia. Ad esempio, nel seguente albero decisionale, le frecce più spesse mostrano il percorso di inferenza per un esempio con i seguenti valori delle funzionalità:
- x = 7
- y = 12
- z = -3
Il percorso di inferenza nella seguente illustrazione passa attraverso tre
condizioni prima di raggiungere la foglia (Zeta).
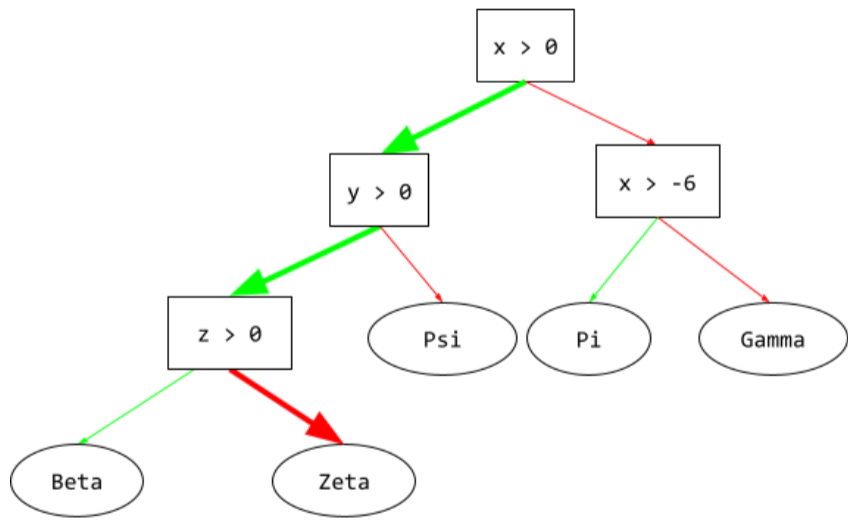
Le tre frecce spesse mostrano il percorso di inferenza.
Per ulteriori informazioni, consulta la sezione Alberi decisionali del corso Decision Forests.
guadagno di informazioni
Nelle foreste decisionali, la differenza tra l'entropia di un nodo e la somma ponderata (in base al numero di esempi) dell'entropia dei relativi nodi secondari. L'entropia di un nodo è l'entropia degli esempi in quel nodo.
Ad esempio, considera i seguenti valori di entropia:
- entropia del nodo principale = 0,6
- entropia di un nodo secondario con 16 esempi pertinenti = 0,2
- entropia di un altro nodo secondario con 24 esempi pertinenti = 0,1
Pertanto, il 40% degli esempi si trova in un nodo secondario e il 60% nell'altro nodo secondario. Pertanto:
- somma dell'entropia ponderata dei nodi secondari = (0,4 * 0,2) + (0,6 * 0,1) = 0,14
Pertanto, l'information gain è:
- guadagno di informazioni = entropia del nodo principale - somma ponderata dell'entropia dei nodi secondari
- information gain = 0,6 - 0,14 = 0,46
La maggior parte degli splitter cerca di creare condizioni che massimizzino l'acquisizione di informazioni.
in-set condition
In un albero decisionale, una condizione che verifica la presenza di un elemento in un insieme di elementi. Ad esempio, la seguente è una condizione in-set:
house-style in [tudor, colonial, cape]
Durante l'inferenza, se il valore della funzionalità
dello stile della casa è tudor, colonial o cape, questa condizione restituisce Sì. Se
il valore della funzionalità di stile della casa è un altro (ad esempio, ranch),
questa condizione restituisce No.
Le condizioni in-set in genere portano ad alberi decisionali più efficienti rispetto alle condizioni che testano le funzionalità codificate one-hot.
L
foglia
Qualsiasi endpoint in un albero decisionale. A differenza di una condizione, una foglia non esegue un test. Una foglia è una possibile previsione. Una foglia è anche il nodo terminale di un percorso di inferenza.
Ad esempio, il seguente albero decisionale contiene tre foglie:

Per ulteriori informazioni, consulta la sezione Alberi decisionali del corso Decision Forests.
No
nodo (albero decisionale)
In un albero decisionale, qualsiasi condizione o foglia.
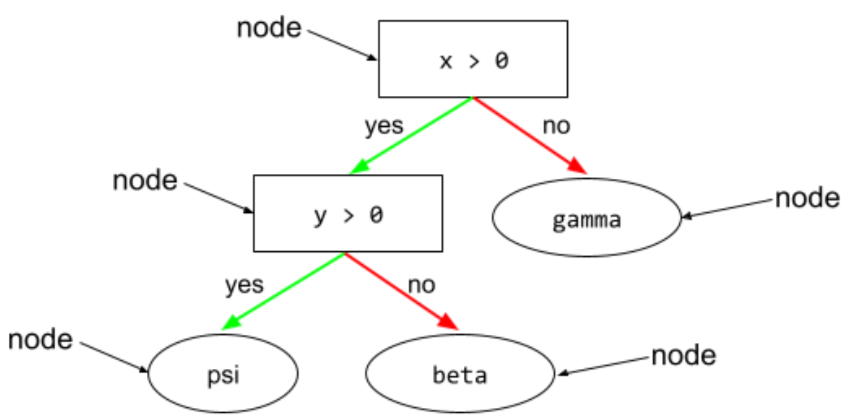
Per ulteriori informazioni, consulta la sezione Alberi decisionali del corso Decision Forests.
condizione non binaria
Una condizione contenente più di due risultati possibili. Ad esempio, la seguente condizione non binaria contiene tre possibili risultati:
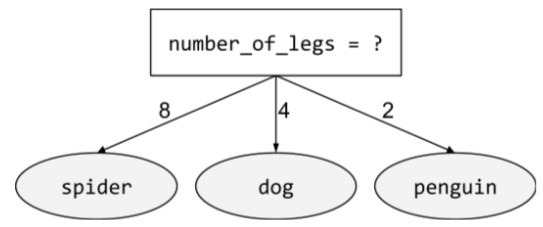
Per ulteriori informazioni, consulta la sezione Tipi di condizioni del corso Decision Forests.
O
condizione obliqua
In un albero decisionale, una condizione che coinvolge più di una caratteristica. Ad esempio, se altezza e larghezza sono entrambe caratteristiche, la seguente è una condizione obliqua:
height > width
Contrasto con la condizione allineata all'asse.
Per ulteriori informazioni, consulta la sezione Tipi di condizioni del corso Decision Forests.
valutazione out-of-bag (valutazione OOB)
Un meccanismo per valutare la qualità di una foresta decisionale testando ogni albero decisionale rispetto agli esempi non utilizzati durante l'addestramento di quell'albero decisionale. Ad esempio, nel diagramma seguente, nota che il sistema addestra ogni albero decisionale su circa due terzi degli esempi e poi lo valuta in base al terzo rimanente degli esempi.
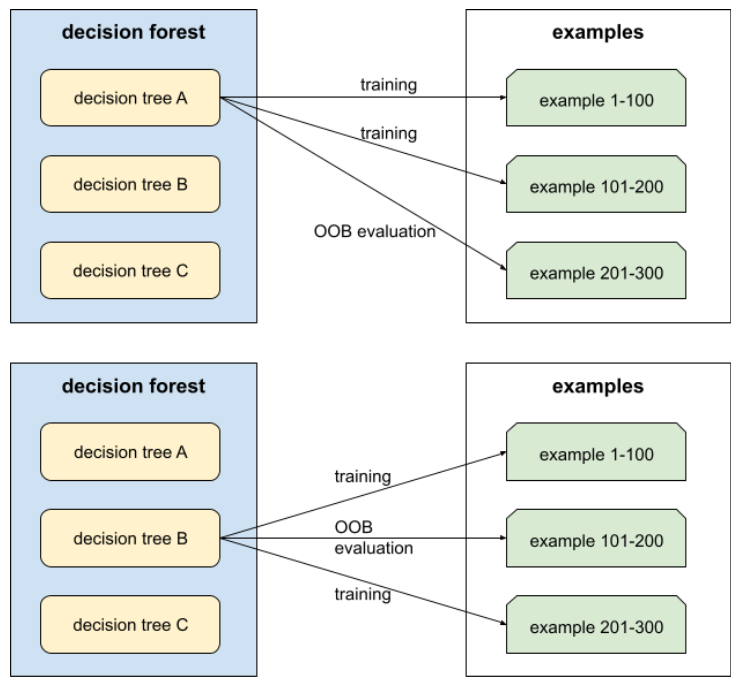
La valutazione out-of-bag è un'approssimazione efficiente dal punto di vista computazionale e conservativa del meccanismo di cross-validation. Nella convalida incrociata, viene addestrato un modello per ogni round di convalida incrociata (ad esempio, vengono addestrati 10 modelli in una convalida incrociata a 10 fold). Con la valutazione OOB, viene addestrato un singolo modello. Poiché il bagging esclude alcuni dati da ogni albero durante l'addestramento, la valutazione OOB può utilizzare questi dati per approssimare la convalida incrociata.
Per ulteriori informazioni, consulta Valutazione out-of-bag nel corso Decision Forests.
P
importanza delle variabili di permutazione
Un tipo di importanza delle variabili che valuta l'aumento dell'errore di previsione di un modello dopo la permutazione dei valori della caratteristica. L'importanza delle variabili di permutazione è una metrica indipendente dal modello.
R
foresta casuale
Un ensemble di alberi decisionali in cui ogni albero decisionale viene addestrato con un rumore casuale specifico, ad esempio il bagging.
Le foreste casuali sono un tipo di foresta decisionale.
Per ulteriori informazioni, consulta la sezione Random Forest del corso Decision Forests.
root
Il nodo iniziale (la prima condizione) in un albero decisionale. Per convenzione, i diagrammi posizionano la radice nella parte superiore dell'albero decisionale. Ad esempio:
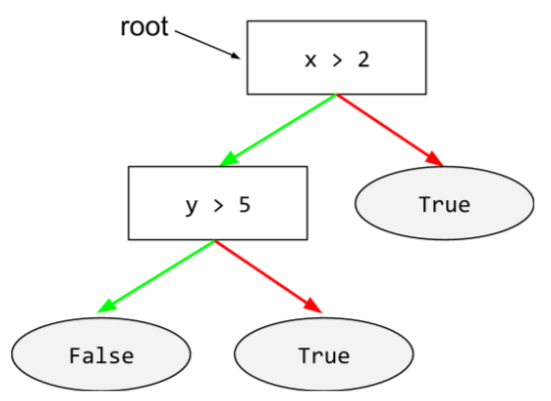
S
campionamento con reinserimento
Un metodo di selezione di elementi da un insieme di elementi candidati in cui lo stesso elemento può essere selezionato più volte. La frase "con reintegro" significa che dopo ogni selezione, l'elemento selezionato viene restituito al pool di elementi candidati. Il metodo inverso, campionamento senza reinserimento, significa che un elemento candidato può essere scelto solo una volta.
Ad esempio, considera il seguente insieme di frutti:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Supponiamo che il sistema scelga casualmente fig come primo elemento.
Se utilizzi il campionamento con reinserimento, il sistema sceglie il secondo elemento dal seguente insieme:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango}Sì, è lo stesso set di prima, quindi il sistema potrebbe potenzialmente
scegliere di nuovo fig.
Se utilizzi il campionamento senza sostituzione, una volta scelto, un campione non può essere
scelto di nuovo. Ad esempio, se il sistema sceglie in modo casuale fig come
primo campione, fig non può essere scelto di nuovo. Pertanto, il sistema
sceglie il secondo campione dal seguente insieme (ridotto):
fruit = {kiwi, apple, pear, cherry, lime, mango}restringimento
Un iperparametro nel gradient boosting che controlla l'overfitting. La contrazione nel boosting del gradiente è analoga al tasso di apprendimento nella discesa del gradiente. Il restringimento è un valore decimale compreso tra 0,0 e 1,0. Un valore di contrazione più basso riduce l'overfitting più di un valore di contrazione più alto.
Spalato
In un albero decisionale, un altro nome per una condizione.
splitter
Durante l'addestramento di un albero decisionale, la routine (e l'algoritmo) responsabile della ricerca della migliore condizione in ogni nodo.
T
test
In un albero decisionale, un altro nome per una condizione.
soglia (per gli alberi decisionali)
In una condizione allineata all'asse, il valore con cui viene confrontata una caratteristica. Ad esempio, 75 è il valore soglia nella seguente condizione:
grade >= 75
Per saperne di più, consulta Splitter esatto per la classificazione binaria con funzionalità numeriche nel corso Decision Forests.
V
importanza delle variabili
Un insieme di punteggi che indica l'importanza relativa di ciascuna caratteristica per il modello.
Ad esempio, considera un albero decisionale che stima i prezzi delle case. Supponiamo che questo albero decisionale utilizzi tre caratteristiche: taglia, età e stile. Se un insieme di importanze delle variabili per le tre caratteristiche viene calcolato come {size=5.8, age=2.5, style=4.7}, la taglia è più importante per l'albero decisionale rispetto all'età o allo stile.
Esistono diverse metriche di importanza delle variabili, che possono fornire agli esperti di ML informazioni su diversi aspetti dei modelli.
M
saggezza della folla
L'idea che la media delle opinioni o delle stime di un ampio gruppo di persone ("la folla") spesso produca risultati sorprendentemente buoni. Ad esempio, considera un gioco in cui le persone devono indovinare il numero di caramelle gommose contenute in un grande barattolo. Anche se la maggior parte delle stime individuali sarà imprecisa, è stato dimostrato empiramente che la media di tutte le stime è sorprendentemente vicina al numero effettivo di caramelle nel barattolo.
Gli ensemble sono l'equivalente software della saggezza della folla. Anche se i singoli modelli fanno previsioni molto imprecise, la media delle previsioni di molti modelli spesso genera previsioni sorprendentemente buone. Ad esempio, anche se un albero decisionale individuale potrebbe fare previsioni errate, una foresta decisionale spesso fa previsioni molto accurate.