این صفحه شامل اصطلاحات واژه نامه Decision Forests است. برای همه اصطلاحات واژه نامه، اینجا را کلیک کنید .
الف
نمونه گیری ویژگی
تاکتیکی برای آموزش یک جنگل تصمیم که در آن هر درخت تصمیم تنها یک زیرمجموعه تصادفی از ویژگی های ممکن را در هنگام یادگیری شرایط در نظر می گیرد. به طور کلی، زیر مجموعه متفاوتی از ویژگی ها برای هر گره نمونه برداری می شود. در مقابل، هنگام آموزش یک درخت تصمیم بدون نمونه گیری ویژگی، تمام ویژگی های ممکن برای هر گره در نظر گرفته می شود.
وضعیت هم تراز با محور
در درخت تصمیم ، شرایطی که فقط شامل یک ویژگی است. برای مثال، اگر area یک ویژگی است، شرایط زیر یک شرط تراز محور است:
area > 200
کنتراست با حالت مایل .
ب
بسته بندی
روشی برای آموزش یک گروه که در آن هر مدل سازنده بر روی یک زیرمجموعه تصادفی از نمونههای آموزشی نمونهبرداری شده با جایگزینی تمرین میکند. به عنوان مثال، یک جنگل تصادفی مجموعه ای از درختان تصمیم گیری است که با کیسه بندی آموزش دیده اند.
اصطلاح bagging مخفف b ootstrap agg regat ing است .
برای اطلاعات بیشتر به جنگل های تصادفی در دوره جنگل های تصمیم گیری مراجعه کنید.
شرایط باینری
در درخت تصمیم ، شرایطی که فقط دو نتیجه ممکن دارد، معمولاً بله یا خیر . به عنوان مثال، شرایط زیر یک شرط باینری است:
temperature >= 100
کنتراست با شرط غیر باینری .
برای اطلاعات بیشتر به انواع شرایط در دوره Decision Forests مراجعه کنید.
سی
وضعیت
در درخت تصمیم ، هر گره ای که آزمایشی را انجام می دهد. به عنوان مثال، درخت تصمیم زیر شامل دو شرط است: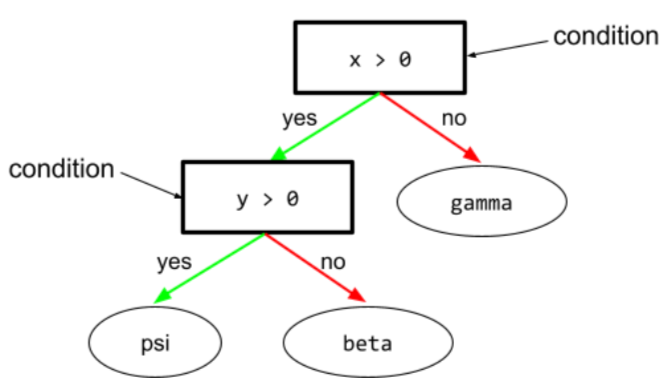
به یک وضعیت، تقسیم یا آزمایش نیز گفته می شود.
شرایط کنتراست با برگ
همچنین ببینید:
برای اطلاعات بیشتر به انواع شرایط در دوره Decision Forests مراجعه کنید.
D
جنگل تصمیم
مدلی که از چندین درخت تصمیم ایجاد شده است. یک جنگل تصمیم گیری با تجمیع پیش بینی های درختان تصمیم خود پیش بینی می کند. انواع محبوب جنگلهای تصمیمگیری شامل جنگلهای تصادفی و درختان تقویتشده با گرادیان است.
برای اطلاعات بیشتر به بخش Decision Forests در دوره Decision Forests مراجعه کنید.
درخت تصمیم
یک مدل یادگیری تحت نظارت متشکل از مجموعهای از شرایط و برگهایی که به صورت سلسله مراتبی سازماندهی شدهاند. به عنوان مثال، شکل زیر یک درخت تصمیم است:
E
آنتروپی
در تئوری اطلاعات ، توصیفی از غیرقابل پیشبینی بودن توزیع احتمال است. متناوباً، آنتروپی نیز به این صورت تعریف میشود که هر مثال حاوی چه مقدار اطلاعات است. یک توزیع دارای بالاترین آنتروپی ممکن است زمانی که همه مقادیر یک متغیر تصادفی به یک اندازه محتمل باشند.
آنتروپی یک مجموعه با دو مقدار ممکن "0" و "1" (به عنوان مثال، برچسب ها در یک مسئله طبقه بندی باینری ) فرمول زیر را دارد:
H = -p log p - q log q = -p log p - (1-p) * log (1-p)
کجا:
- H آنتروپی است.
- p کسری از مثال های "1" است.
- q کسری از مثال های "0" است. توجه داشته باشید که q = (1 - p)
- log به طور کلی log 2 است. در این حالت واحد آنتروپی کمی است.
برای مثال موارد زیر را فرض کنید:
- 100 مثال حاوی مقدار "1" است
- 300 مثال حاوی مقدار "0" هستند
بنابراین، مقدار آنتروپی:
- p = 0.25
- q = 0.75
- H = (-0.25)log 2 (0.25) - (0.75)log 2 (0.75) = 0.81 بیت در هر مثال
مجموعه ای که کاملاً متعادل باشد (مثلاً 200 "0" و 200 "1") آنتروپی 1.0 بیت در هر مثال خواهد داشت. وقتی یک مجموعه نامتعادل تر می شود، آنتروپی آن به سمت 0.0 حرکت می کند.
در درختهای تصمیم ، آنتروپی به فرمولبندی به دست آوردن اطلاعات کمک میکند تا به تقسیمکننده کمک کند شرایط را در طول رشد درخت تصمیم طبقهبندی انتخاب کند.
مقایسه آنتروپی با:
- ناخالصی جینی
- تابع از دست دادن آنتروپی متقابل
آنتروپی اغلب آنتروپی شانون نامیده می شود.
برای اطلاعات بیشتر به Exact splitter برای طبقه بندی باینری با ویژگی های عددی در دوره Decision Forests مراجعه کنید.
اف
اهمیت ویژگی ها
مترادف برای اهمیت متغیر .
جی
ناخالصی جینی
متریک مشابه آنتروپی . اسپلیترها از مقادیر به دست آمده از ناخالصی جینی یا آنتروپی برای ایجاد شرایط برای درختان تصمیم طبقه بندی استفاده می کنند. کسب اطلاعات از آنتروپی به دست می آید. هیچ عبارت معادل پذیرفته شده جهانی برای متریک مشتق شده از ناخالصی جینی وجود ندارد. با این حال، این معیار نامشخص به اندازه کسب اطلاعات مهم است.
به ناخالصی جینی شاخص جینی یا به سادگی جینی نیز گفته می شود.
درختان شیب تقویت شده (تصمیم گیری) (GBT)
نوعی جنگل تصمیم گیری که در آن:
- آموزش متکی بر افزایش گرادیان است.
- مدل ضعیف درخت تصمیم است.
برای اطلاعات بیشتر، درختهای تصمیمگیری با گرادیان را در دوره جنگلهای تصمیمگیری ببینید.
تقویت گرادیان
یک الگوریتم آموزشی که در آن مدلهای ضعیف برای بهبود مکرر کیفیت (کاهش ضرر) یک مدل قوی آموزش داده میشوند. به عنوان مثال، یک مدل ضعیف می تواند یک مدل درخت تصمیم خطی یا کوچک باشد. مدل قوی مجموع تمام مدل های ضعیف آموزش دیده قبلی می شود.
در سادهترین شکل تقویت گرادیان، در هر تکرار، یک مدل ضعیف برای پیشبینی گرادیان تلفات مدل قوی آموزش داده میشود. سپس، خروجی مدل قوی با کم کردن گرادیان پیشبینیشده، مشابه شیب نزول ، بهروزرسانی میشود.
کجا:
- $F_{0}$ اولین مدل قوی است.
- $F_{i+1}$ مدل قوی بعدی است.
- $F_{i}$ مدل قوی فعلی است.
- $\xi$ مقداری بین 0.0 و 1.0 به نام انقباض است که مشابه نرخ یادگیری در نزول گرادیان است.
- $f_{i}$ مدل ضعیفی است که برای پیشبینی گرادیان ضرر F_{i}$ آموزش داده شده است.
تغییرات مدرن تقویت گرادیان همچنین مشتق دوم (Hessian) از دست دادن را در محاسبه خود شامل می شود.
درخت های تصمیم معمولاً به عنوان مدل های ضعیف در تقویت گرادیان استفاده می شوند. درختان با شیب تقویت شده (تصمیم گیری) را ببینید.
من
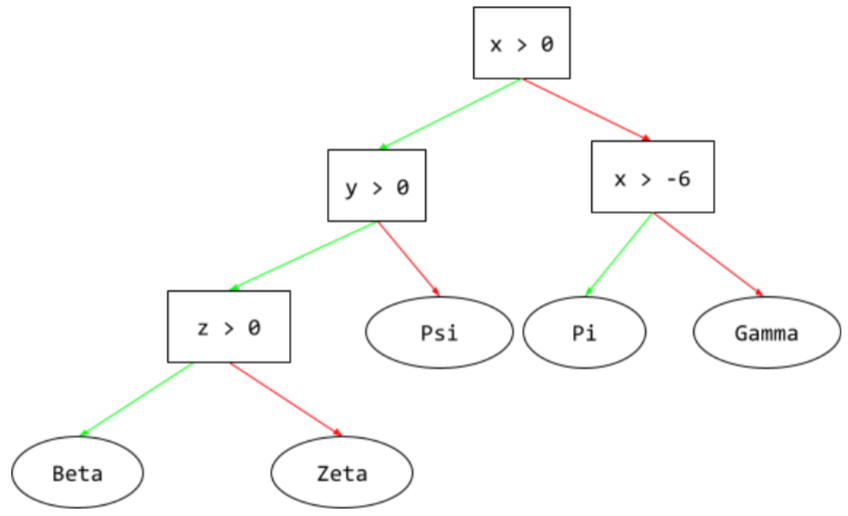
مسیر استنتاج
در درخت تصمیم , در طول استنتاج , مسیری که یک مثال خاص از ریشه به شرایط دیگر طی می کند و با یک برگ ختم می شود . به عنوان مثال، در درخت تصمیم زیر، فلشهای ضخیمتر مسیر استنتاج را برای یک مثال با مقادیر ویژگی زیر نشان میدهند:
- x = 7
- y = 12
- z = -3
مسیر استنتاج در تصویر زیر قبل از رسیدن به برگ ( Zeta ) از سه حالت عبور می کند.
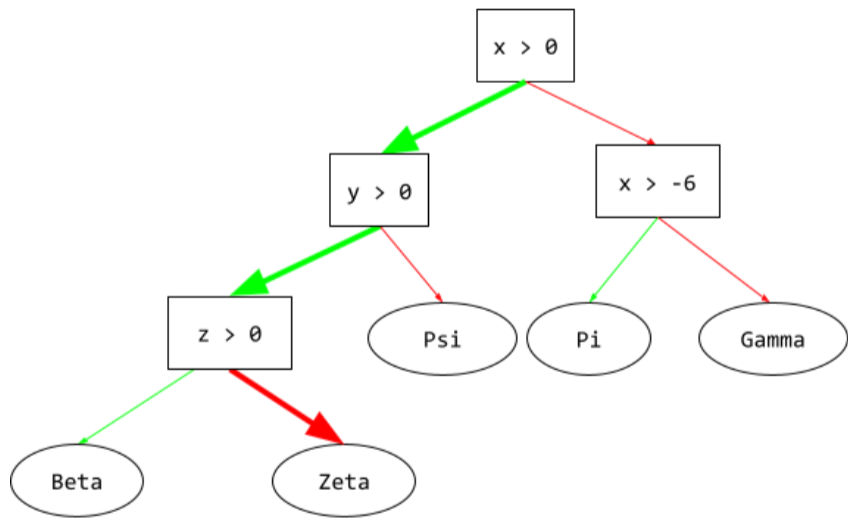
سه فلش ضخیم مسیر استنتاج را نشان می دهد.
برای اطلاعات بیشتر به درختان تصمیم در دوره Decision Forests مراجعه کنید.
کسب اطلاعات
در جنگلهای تصمیم ، تفاوت بین آنتروپی یک گره و مجموع وزنی (براساس تعداد مثال) از آنتروپی گرههای فرزند آن است. آنتروپی یک گره، آنتروپی نمونه های آن گره است.
به عنوان مثال، مقادیر آنتروپی زیر را در نظر بگیرید:
- آنتروپی گره والد = 0.6
- آنتروپی یک گره فرزند با 16 مثال مرتبط = 0.2
- آنتروپی یک گره فرزند دیگر با 24 مثال مرتبط = 0.1
بنابراین 40 درصد از نمونه ها در یک گره فرزند و 60 درصد در گره فرزند دیگر هستند. بنابراین:
- مجموع آنتروپی وزنی گره های فرزند = (0.4 * 0.2) + (0.6 * 0.1) = 0.14
بنابراین، به دست آوردن اطلاعات این است:
- افزایش اطلاعات = آنتروپی گره والد - مجموع وزنی آنتروپی گره های فرزند
- افزایش اطلاعات = 0.6 - 0.14 = 0.46
بیشتر اسپلیترها به دنبال ایجاد شرایطی هستند که کسب اطلاعات را به حداکثر برسانند.
شرایط در مجموعه
در درخت تصمیم ، شرایطی که وجود یک آیتم را در مجموعه ای از آیتم ها آزمایش می کند. به عنوان مثال، شرایط زیر یک شرط در مجموعه است:
house-style in [tudor, colonial, cape]
در طول استنتاج، اگر مقدار ویژگی سبک خانه tudor یا colonial یا cape باشد، این شرط به بله ارزیابی می شود. اگر مقدار ویژگی house-style چیز دیگری باشد (مثلاً ranch )، این شرط به No ارزیابی میشود.
شرایط درونتنظیمی معمولاً به درختهای تصمیمگیری کارآمدتری نسبت به شرایطی منجر میشود که ویژگیهای کدگذاری شده یکبار را آزمایش میکنند.
L
برگ
هر نقطه پایانی در درخت تصمیم . بر خلاف شرایط ، یک برگ آزمایشی را انجام نمی دهد. بلکه یک برگ یک پیش بینی ممکن است. یک برگ همچنین گره پایانی یک مسیر استنتاج است.
به عنوان مثال، درخت تصمیم زیر شامل سه برگ است:
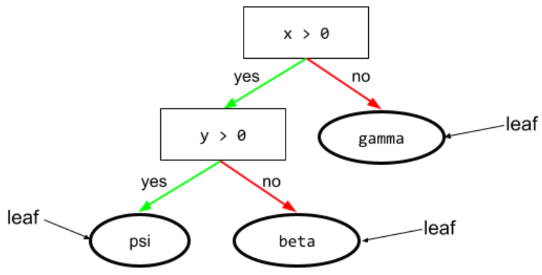
برای اطلاعات بیشتر به درختان تصمیم در دوره Decision Forests مراجعه کنید.
ن
گره (درخت تصمیم)
در درخت تصمیم ، هر شرایط یا برگ .
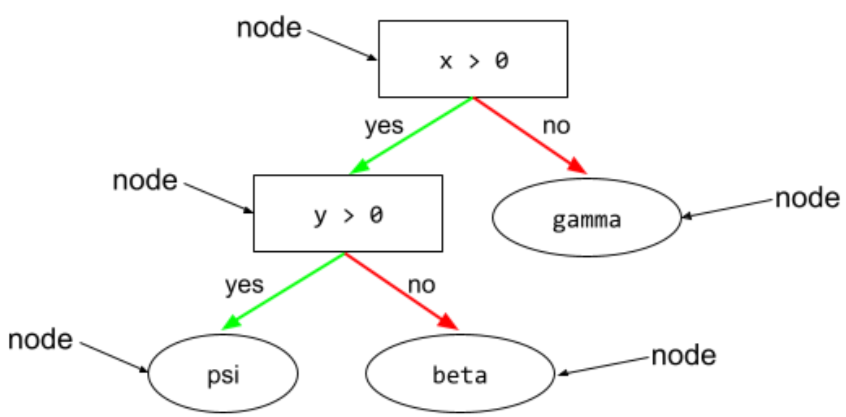
برای اطلاعات بیشتر Decision Trees را در دوره Decision Forests ببینید.
شرایط غیر باینری
شرایطی که شامل بیش از دو پیامد احتمالی است. برای مثال، شرط غیر باینری زیر شامل سه نتیجه ممکن است:
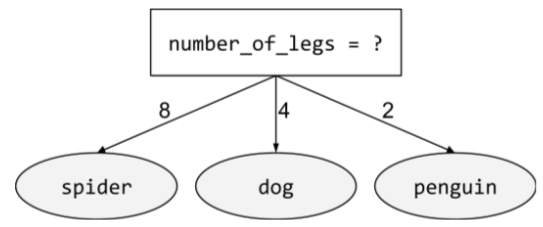
برای اطلاعات بیشتر به انواع شرایط در دوره Decision Forests مراجعه کنید.
O
حالت مایل
در درخت تصمیم ، شرایطی که شامل بیش از یک ویژگی است. به عنوان مثال، اگر ارتفاع و عرض هر دو ویژگی هستند، در این صورت شرایط زیر یک شرط مورب است:
height > width
کنتراست با شرایط تراز محور .
برای اطلاعات بیشتر به انواع شرایط در دوره Decision Forests مراجعه کنید.
ارزیابی خارج از کیف (ارزیابی OOB)
مکانیزمی برای ارزیابی کیفیت یک جنگل تصمیم با آزمایش هر درخت تصمیم در برابر نمونه هایی که در طول آموزش آن درخت تصمیم استفاده نشده است. به عنوان مثال، در نمودار زیر، توجه کنید که سیستم هر درخت تصمیم را در حدود دو سوم مثال ها آموزش می دهد و سپس با یک سوم نمونه های باقی مانده ارزیابی می کند.
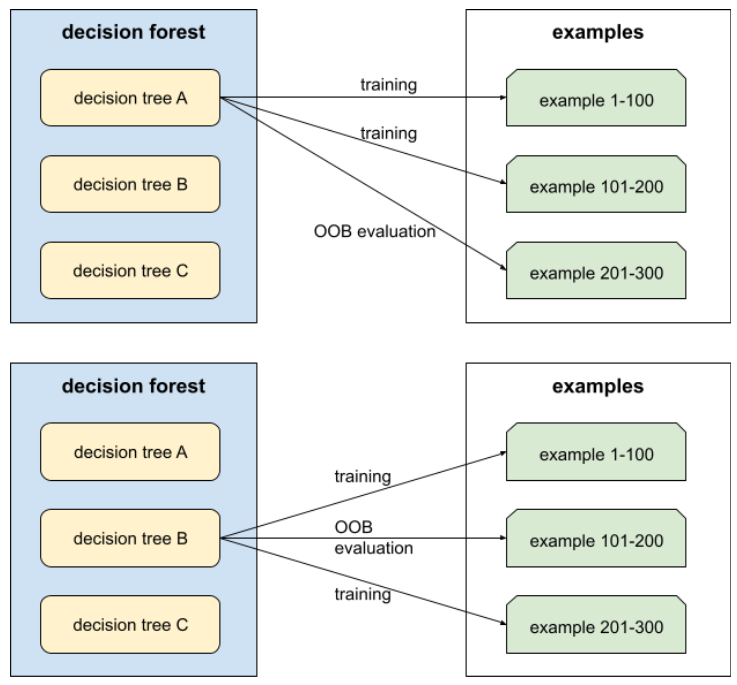
ارزیابی خارج از کیسه یک تقریب محاسباتی کارآمد و محافظه کارانه از مکانیسم اعتبارسنجی متقابل است. در اعتبارسنجی متقاطع، برای هر دور اعتبار سنجی متقابل یک مدل آموزش داده می شود (مثلاً 10 مدل در یک اعتبارسنجی متقاطع 10 برابری آموزش داده می شوند). با ارزیابی OOB، یک مدل واحد آموزش داده می شود. از آنجایی که بستهبندی برخی از دادهها را از هر درخت در طول آموزش نگه میدارد، ارزیابی OOB میتواند از آن دادهها برای اعتبارسنجی تقریبی استفاده کند.
برای اطلاعات بیشتر ، ارزیابی خارج از کیسه را در دوره Decision Forests ببینید.
پ
اهمیت متغیر جایگشت
نوعی از اهمیت متغیر که افزایش خطای پیشبینی یک مدل را پس از تغییر مقادیر ویژگی ارزیابی میکند. اهمیت متغیر جایگشت یک متریک مستقل از مدل است.
آر
جنگل تصادفی
مجموعهای از درختهای تصمیم که در آن هر درخت تصمیم با نویز تصادفی خاصی مانند کیسهبندی آموزش داده میشود.
جنگل های تصادفی نوعی جنگل تصمیم گیری هستند.
برای اطلاعات بیشتر به جنگل تصادفی در دوره جنگلهای تصمیمگیری مراجعه کنید.
ریشه
گره شروع ( شرط اول) در درخت تصمیم . طبق قرارداد، نمودارها ریشه را در بالای درخت تصمیم قرار می دهند. به عنوان مثال:
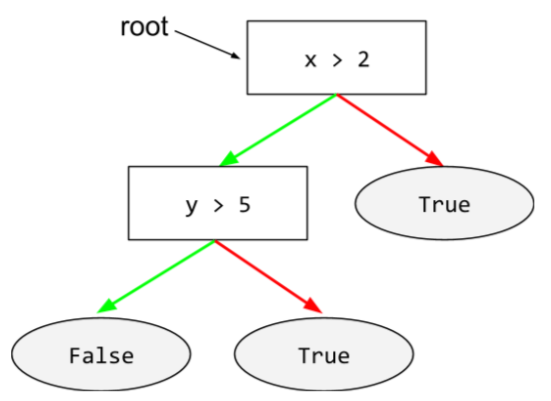
اس
نمونه برداری با جایگزینی
روشی برای انتخاب اقلام از مجموعه ای از اقلام نامزد که در آن می توان یک مورد را چندین بار انتخاب کرد. عبارت «با جایگزینی» به این معنی است که پس از هر انتخاب، آیتم انتخاب شده به مجموعه اقلام نامزد بازگردانده می شود. روش معکوس، نمونه برداری بدون جایگزینی ، به این معنی است که یک مورد کاندید فقط یک بار قابل انتخاب است.
به عنوان مثال، مجموعه میوه زیر را در نظر بگیرید:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango} فرض کنید که سیستم به طور تصادفی fig به عنوان اولین مورد انتخاب می کند. اگر از نمونه برداری با جایگزینی استفاده می کنید، سیستم مورد دوم را از مجموعه زیر انتخاب می کند:
fruit = {kiwi, apple, pear, fig, cherry, lime, mango} بله، این همان مجموعه قبلی است، بنابراین سیستم به طور بالقوه می تواند دوباره fig انتخاب کند.
اگر از نمونه برداری بدون جایگزینی استفاده می شود، پس از انتخاب، نمونه را نمی توان دوباره انتخاب کرد. به عنوان مثال، اگر سیستم به طور تصادفی fig به عنوان اولین نمونه انتخاب کند، آنگاه نمی توان دوباره fig را انتخاب کرد. بنابراین، سیستم نمونه دوم را از مجموعه زیر (کاهش یافته) انتخاب می کند:
fruit = {kiwi, apple, pear, cherry, lime, mango}انقباض
یک هایپرپارامتر در تقویت گرادیان که اضافه برازش را کنترل می کند. انقباض در تقویت گرادیان مشابه نرخ یادگیری در نزول گرادیان است. Shrinkage یک مقدار اعشاری بین 0.0 و 1.0 است. مقدار انقباض کمتر، بیش از حد برازش را نسبت به مقدار انقباض بزرگتر کاهش می دهد.
تقسیم
در درخت تصمیم ، نام دیگری برای یک شرط است.
شکافنده
هنگام آموزش درخت تصمیم ، روال (و الگوریتم) مسئول یافتن بهترین شرایط در هر گره است.
تی
تست کنید
در درخت تصمیم ، نام دیگری برای یک شرط است.
آستانه (برای درختان تصمیم)
در شرایط تراز محور ، مقداری که یک ویژگی با آن مقایسه می شود. به عنوان مثال، 75 مقدار آستانه در شرایط زیر است:
grade >= 75
برای اطلاعات بیشتر به Exact splitter برای طبقه بندی باینری با ویژگی های عددی در دوره Decision Forests مراجعه کنید.
V
اهمیت های متغیر
مجموعه ای از امتیازات که اهمیت نسبی هر ویژگی را برای مدل نشان می دهد.
به عنوان مثال، درخت تصمیم گیری را در نظر بگیرید که قیمت خانه را تخمین می زند. فرض کنید این درخت تصمیم از سه ویژگی استفاده می کند: اندازه، سن و سبک. اگر مجموعه ای از اهمیت های متغیر برای سه ویژگی به صورت {size=5.8، age=2.5، style=4.7} محاسبه شود، آنگاه اندازه برای درخت تصمیم مهم تر از سن یا سبک است.
معیارهای اهمیت متغیر متفاوتی وجود دارد که می تواند کارشناسان ML را در مورد جنبه های مختلف مدل ها آگاه کند.
دبلیو
حکمت جمعیت
این ایده که میانگین گرفتن نظرات یا تخمینهای گروه بزرگی از مردم ("جمعیت") اغلب نتایج شگفتآوری خوبی دارد. به عنوان مثال، یک بازی را در نظر بگیرید که در آن افراد تعداد دانه های ژله ای را که در یک شیشه بزرگ بسته بندی شده اند حدس می زنند. اگرچه اکثر حدسهای فردی نادرست خواهند بود، اما میانگین همه حدسها بهطور تجربی به طور شگفتآوری نزدیک به تعداد واقعی دانههای ژله در شیشه است.
گروه ها یک نرم افزار آنالوگ از خرد جمعیت هستند. حتی اگر مدلهای جداگانه پیشبینیهای بسیار نادرستی انجام دهند، میانگینگیری پیشبینیهای بسیاری از مدلها اغلب پیشبینیهای شگفتآور خوبی ایجاد میکند. به عنوان مثال، اگرچه یک درخت تصمیم گیری فردی ممکن است پیش بینی های ضعیفی داشته باشد، یک جنگل تصمیم اغلب پیش بینی های بسیار خوبی انجام می دهد.
