Page Summary
-
Generative models create new data instances, while discriminative models classify existing data.
-
Generative models learn the underlying data distribution, enabling them to generate realistic new samples.
-
Discriminative models focus on distinguishing between data categories by identifying key features.
-
Generative models are generally more complex than discriminative models due to their broader learning task.
-
GANs (Generative Adversarial Networks) are a powerful type of generative model that employ two competing networks for effective training.
What does "generative" mean in the name "Generative Adversarial Network"? "Generative" describes a class of statistical models that contrasts with discriminative models.
Informally:
- Generative models can generate new data instances.
- Discriminative models discriminate between different kinds of data instances.
A generative model could generate new photos of animals that look like real animals, while a discriminative model could tell a dog from a cat. GANs are just one kind of generative model.
More formally, given a set of data instances X and a set of labels Y:
- Generative models capture the joint probability p(X, Y), or just p(X) if there are no labels.
- Discriminative models capture the conditional probability p(Y | X).
A generative model includes the distribution of the data itself, and tells you how likely a given example is. For example, models that predict the next word in a sequence are typically generative models (usually much simpler than GANs) because they can assign a probability to a sequence of words.
A discriminative model ignores the question of whether a given instance is likely, and just tells you how likely a label is to apply to the instance.
Note that this is a very general definition. There are many kinds of generative model. GANs are just one kind of generative model.
Modeling Probabilities
Neither kind of model has to return a number representing a probability. You can model the distribution of data by imitating that distribution.
For example, a discriminative classifier like a decision tree can label an instance without assigning a probability to that label. Such a classifier would still be a model because the distribution of all predicted labels would model the real distribution of labels in the data.
Similarly, a generative model can model a distribution by producing convincing "fake" data that looks like it's drawn from that distribution.
Generative Models Are Hard
Generative models tackle a more difficult task than analogous discriminative models. Generative models have to model more.
A generative model for images might capture correlations like "things that look like boats are probably going to appear near things that look like water" and "eyes are unlikely to appear on foreheads." These are very complicated distributions.
In contrast, a discriminative model might learn the difference between "sailboat" or "not sailboat" by just looking for a few tell-tale patterns. It could ignore many of the correlations that the generative model must get right.
Discriminative models try to draw boundaries in the data space, while generative models try to model how data is placed throughout the space. For example, the following diagram shows discriminative and generative models of handwritten digits:
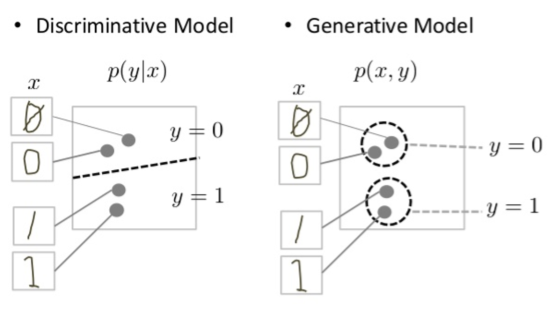
Figure 1: Discriminative and generative models of handwritten digits.
The discriminative model tries to tell the difference between handwritten 0's and 1's by drawing a line in the data space. If it gets the line right, it can distinguish 0's from 1's without ever having to model exactly where the instances are placed in the data space on either side of the line.
In contrast, the generative model tries to produce convincing 1's and 0's by generating digits that fall close to their real counterparts in the data space. It has to model the distribution throughout the data space.
GANs offer an effective way to train such rich models to resemble a real distribution. To understand how they work we'll need to understand the basic structure of a GAN.
Check Your Understanding: Generative vs. Discriminative Models
- Roll three six-sided dice.
- Multiply the roll by a constant w.
- Repeat 100 times and take the average of all the results.