1. Zanim zaczniesz
Z tego ćwiczenia z programowania dowiesz się, czym są sploty i dlaczego są tak przydatne w przypadku zadań związanych z widzeniem komputerowym.
W poprzednim laboratorium utworzyliśmy prostą głęboką sieć neuronową (DNN) do rozpoznawania elementów odzieży. Wymagania były ograniczone, ponieważ odzież musiała być jedynym elementem na zdjęciu i musiała być wyśrodkowana.
Oczywiście nie jest to realistyczny scenariusz. Sieć DNN powinna być w stanie rozpoznawać ubrania na zdjęciach z innymi obiektami lub gdy nie są one umieszczone na pierwszym planie. Aby to zrobić, musisz użyć splotów.
Wymagania wstępne
Ten moduł opiera się na pracy wykonanej w ramach 2 poprzednich modułów: „Hello, World” w systemach uczących się i Tworzenie modelu rozpoznawania obrazów. Zanim przejdziesz dalej, wykonaj te ćwiczenia.
Czego się nauczysz
- Co to są konwolucje
- Jak utworzyć mapę funkcji
- Co to jest łączenie?
Co utworzysz
- Mapa cech obrazu
Czego potrzebujesz
Kod pozostałej części laboratorium znajdziesz w Colab.
Musisz też mieć zainstalowany TensorFlow i biblioteki, które zostały zainstalowane w poprzednim ćwiczeniu.
2. Czym są konwolucje?
Konwolucja to filtr, który przechodzi przez obraz, przetwarza go i wyodrębnia ważne cechy.
Załóżmy, że masz zdjęcie osoby w butach sportowych. Jak wykryć, że na obrazie znajduje się but sportowy? Aby program „widział” obraz jako but sportowy, musisz wyodrębnić ważne cechy i rozmyć te, które nie są istotne. Jest to tzw. mapowanie funkcji.
Proces mapowania funkcji jest teoretycznie prosty. Skanujesz każdy piksel na obrazie, a potem sprawdzasz sąsiednie piksele. Wartości tych pikseli mnożysz przez odpowiednie wagi w filtrze.
Na przykład:
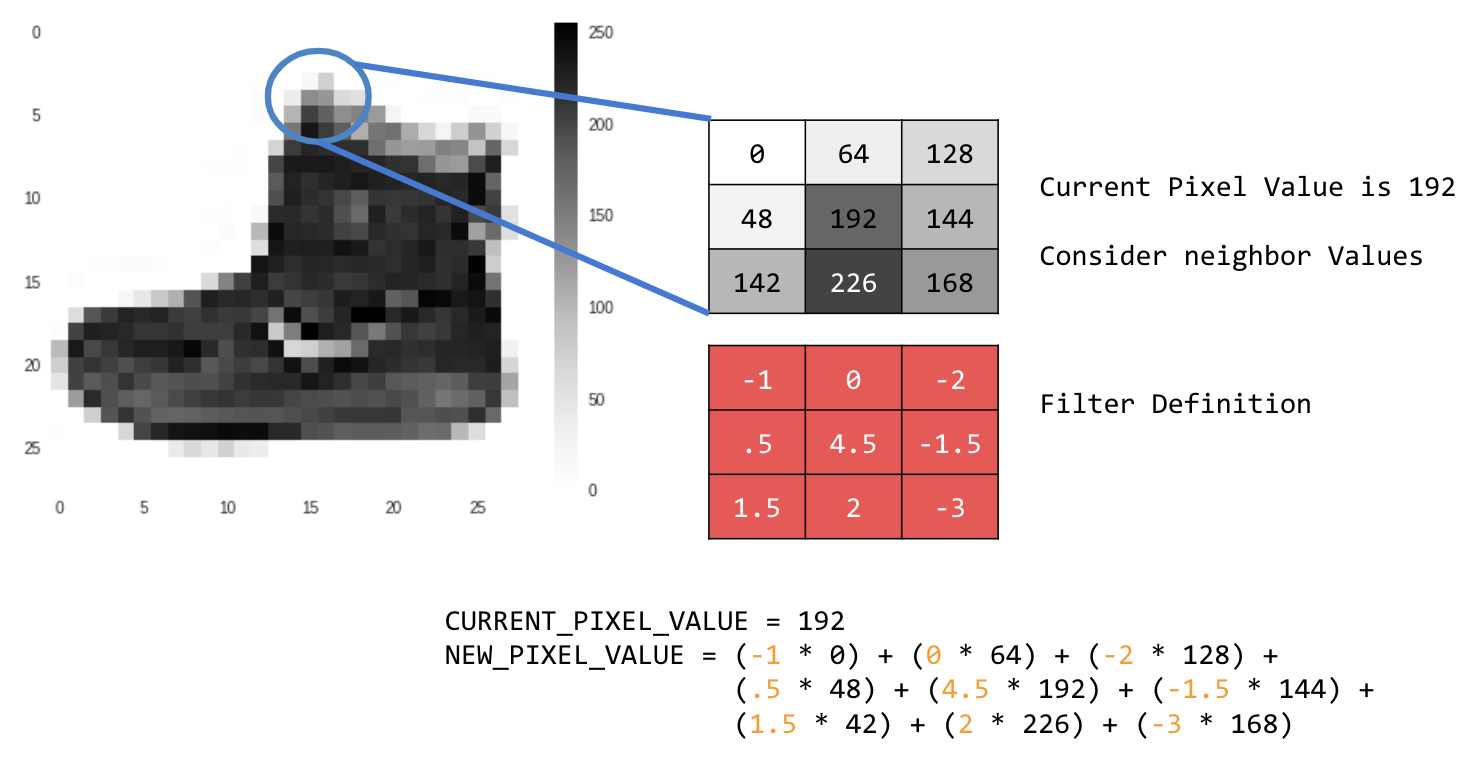
W tym przypadku określono macierz splotu 3x3, czyli jądro obrazu.
Obecna wartość piksela to 192. Wartość nowego piksela możesz obliczyć, sprawdzając wartości sąsiednich pikseli, mnożąc je przez wartości określone w filtrze i ustalając wartość nowego piksela jako wynik końcowy.
Teraz dowiesz się, jak działają sploty, tworząc podstawowy splot na dwuwymiarowym obrazie w odcieniach szarości.
Zrobisz to na przykładzie obrazu ascent z biblioteki SciPy. To ładny, wbudowany obraz z wieloma kątami i liniami.
3. Zacznij pisać kod
Zacznij od zaimportowania bibliotek Pythona i zdjęcia wejścia na szczyt:
import cv2
import numpy as np
from scipy import misc
i = misc.ascent()
Następnie użyj biblioteki Pyplot matplotlib, aby narysować obraz i sprawdzić, jak wygląda:
import matplotlib.pyplot as plt
plt.grid(False)
plt.gray()
plt.axis('off')
plt.imshow(i)
plt.show()

Widać, że to zdjęcie klatki schodowej. Możesz wypróbować i odizolować wiele funkcji. Na przykład są na nim wyraźne linie pionowe.
Obraz jest przechowywany jako tablica NumPy, więc możemy utworzyć przekształcony obraz, po prostu kopiując tę tablicę. Zmienne size_x i size_y będą zawierać wymiary obrazu, dzięki czemu możesz później wykonać na nim pętlę.
i_transformed = np.copy(i)
size_x = i_transformed.shape[0]
size_y = i_transformed.shape[1]
4. Tworzenie macierzy splotu
Najpierw utwórz macierz splotu (lub jądro) jako tablicę 3x3:
# This filter detects edges nicely
# It creates a filter that only passes through sharp edges and straight lines.
# Experiment with different values for fun effects.
#filter = [ [0, 1, 0], [1, -4, 1], [0, 1, 0]]
# A couple more filters to try for fun!
filter = [ [-1, -2, -1], [0, 0, 0], [1, 2, 1]]
#filter = [ [-1, 0, 1], [-2, 0, 2], [-1, 0, 1]]
# If all the digits in the filter don't add up to 0 or 1, you
# should probably do a weight to get it to do so
# so, for example, if your weights are 1,1,1 1,2,1 1,1,1
# They add up to 10, so you would set a weight of .1 if you want to normalize them
weight = 1
Teraz oblicz piksele wyjściowe. Przejdź przez obraz, pozostawiając 1-pikselowy margines, i pomnóż każdy z sąsiadów bieżącego piksela przez wartość zdefiniowaną w filtrze.
Oznacza to, że sąsiadujący z bieżącym pikselem piksel powyżej i po lewej stronie zostanie pomnożony przez element w lewym górnym rogu filtra. Następnie pomnóż wynik przez wagę i upewnij się, że mieści się on w zakresie od 0 do 255.
Na koniec wczytaj nową wartość do przekształconego obrazu:
for x in range(1,size_x-1):
for y in range(1,size_y-1):
output_pixel = 0.0
output_pixel = output_pixel + (i[x - 1, y-1] * filter[0][0])
output_pixel = output_pixel + (i[x, y-1] * filter[0][1])
output_pixel = output_pixel + (i[x + 1, y-1] * filter[0][2])
output_pixel = output_pixel + (i[x-1, y] * filter[1][0])
output_pixel = output_pixel + (i[x, y] * filter[1][1])
output_pixel = output_pixel + (i[x+1, y] * filter[1][2])
output_pixel = output_pixel + (i[x-1, y+1] * filter[2][0])
output_pixel = output_pixel + (i[x, y+1] * filter[2][1])
output_pixel = output_pixel + (i[x+1, y+1] * filter[2][2])
output_pixel = output_pixel * weight
if(output_pixel<0):
output_pixel=0
if(output_pixel>255):
output_pixel=255
i_transformed[x, y] = output_pixel
5. Sprawdzanie wyników
Teraz wykreśl obraz, aby zobaczyć efekt zastosowania filtra:
# Plot the image. Note the size of the axes -- they are 512 by 512
plt.gray()
plt.grid(False)
plt.imshow(i_transformed)
#plt.axis('off')
plt.show()

Sprawdź poniższe wartości filtra i ich wpływ na obraz.
Użycie wartości [-1,0,1,-2,0,2,-1,0,1] daje bardzo wyraźny zestaw linii pionowych:
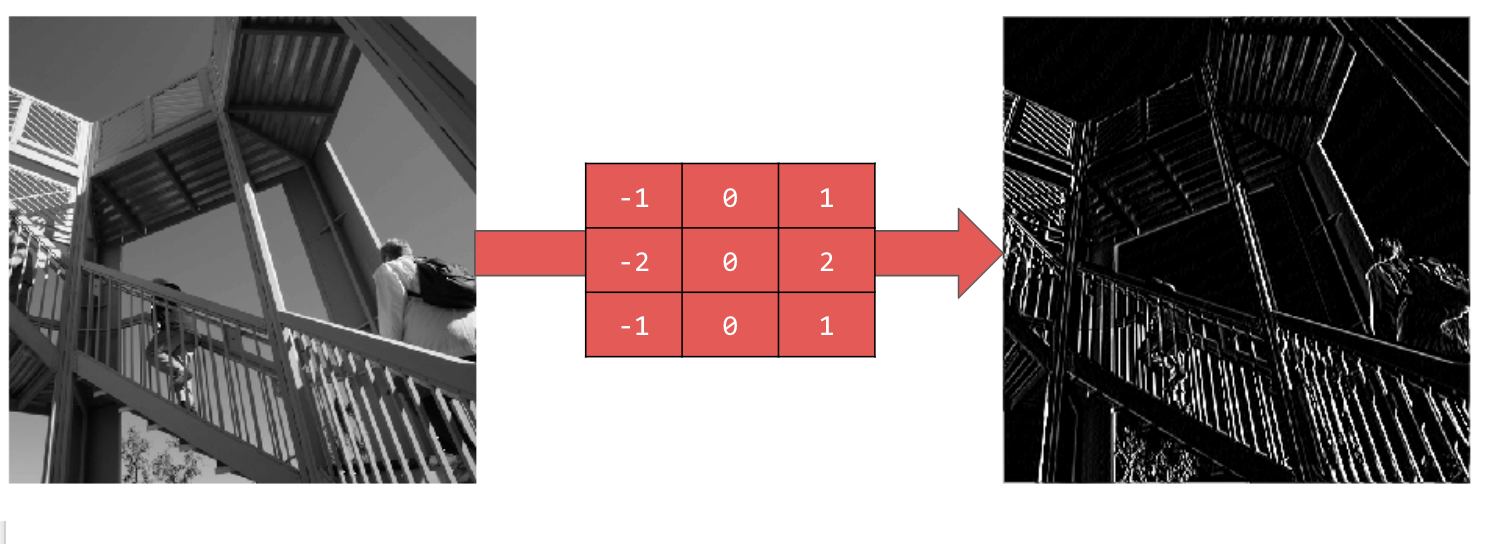
Użycie [-1,-2,-1,0,0,0,1,2,1] daje linie poziome:
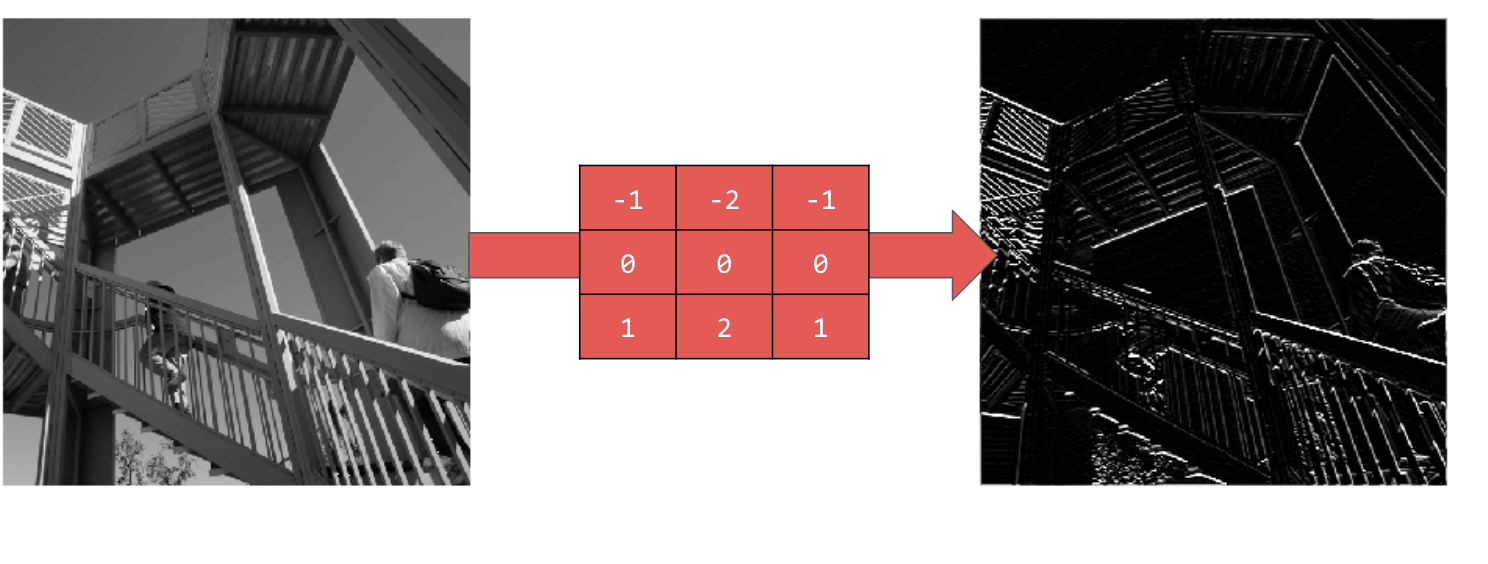
Wypróbuj różne wartości. Wypróbuj też filtry o różnych rozmiarach, np. 5x5 lub 7x7.
6. Omówienie puli
Znasz już najważniejsze cechy obrazu. Co dalej? Jak wykorzystujesz powstałą mapę cech do klasyfikowania obrazów?
Podobnie jak konwolucje, pooling bardzo pomaga w wykrywaniu cech. Warstwy puli zmniejszają ogólną ilość informacji na obrazie, zachowując jednocześnie wykryte cechy.
Istnieje kilka różnych typów puli, ale Ty będziesz używać puli o nazwie Maksymalna (Max).
Przejdź przez obraz i w każdym punkcie rozważ piksel oraz jego bezpośrednich sąsiadów po prawej stronie, poniżej i po prawej stronie poniżej. Wybierz największą z nich (stąd nazwa maksymalne uśrednianie) i wczytaj ją do nowego obrazu. Nowy obraz będzie więc 4 razy mniejszy od starego. 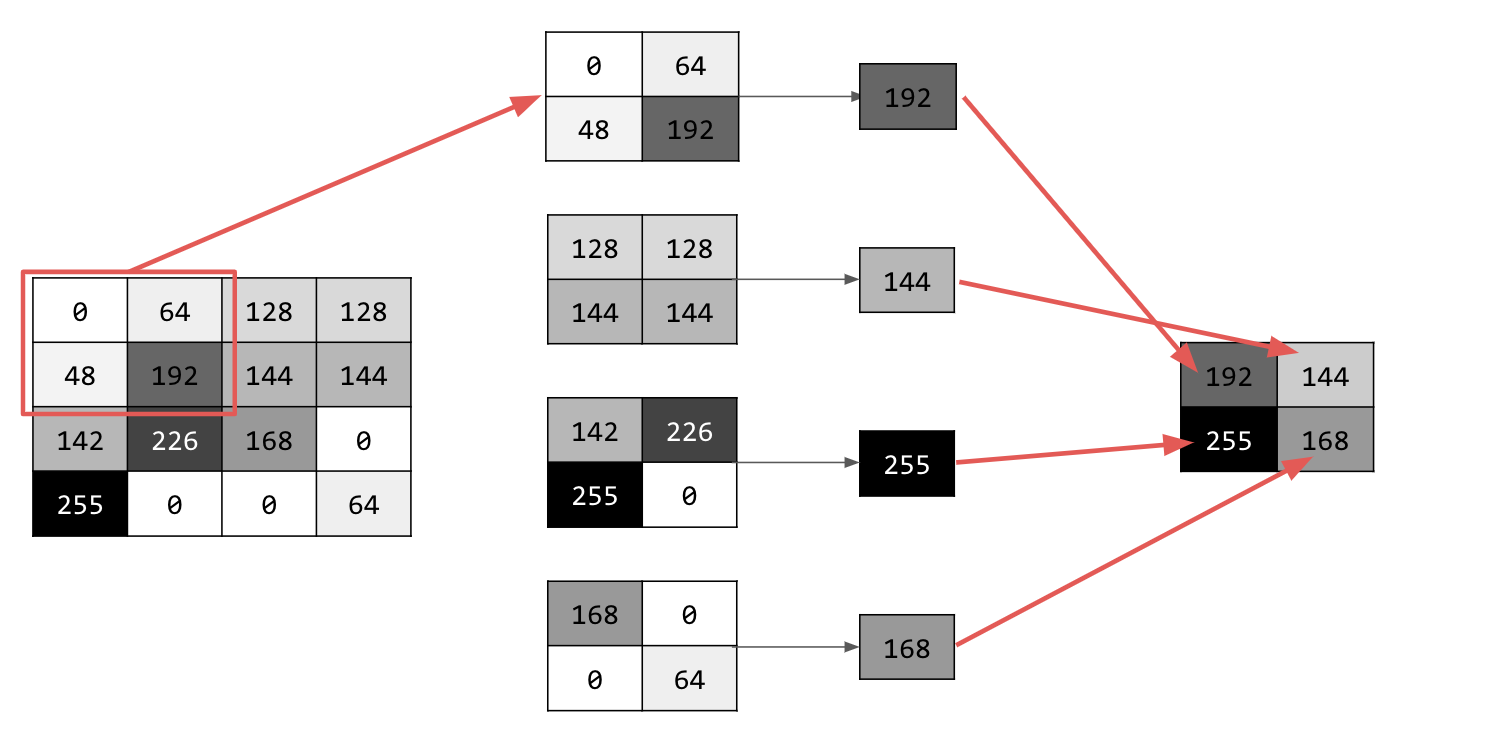
7. Pisanie kodu na potrzeby puli
Poniższy kod pokazuje pulę (2, 2). Uruchom go, aby zobaczyć dane wyjściowe.
Jak widać, obraz ma rozmiar 1/4 oryginału, ale zachował wszystkie cechy.
new_x = int(size_x/2)
new_y = int(size_y/2)
newImage = np.zeros((new_x, new_y))
for x in range(0, size_x, 2):
for y in range(0, size_y, 2):
pixels = []
pixels.append(i_transformed[x, y])
pixels.append(i_transformed[x+1, y])
pixels.append(i_transformed[x, y+1])
pixels.append(i_transformed[x+1, y+1])
pixels.sort(reverse=True)
newImage[int(x/2),int(y/2)] = pixels[0]
# Plot the image. Note the size of the axes -- now 256 pixels instead of 512
plt.gray()
plt.grid(False)
plt.imshow(newImage)
#plt.axis('off')
plt.show()

Zwróć uwagę na osie tego wykresu. Obraz ma teraz wymiary 256 x 256 pikseli, czyli jest 4 razy mniejszy niż pierwotnie, a wykryte cechy zostały wzmocnione, mimo że obraz zawiera teraz mniej danych.
8. Gratulacje
Udało Ci się utworzyć pierwszy model widzenia komputerowego. Aby dowiedzieć się, jak jeszcze bardziej ulepszyć modele widzenia komputerowego, przejdź do artykułu Tworzenie konwolucyjnych sieci neuronowych (CNN) w celu ulepszenia widzenia komputerowego.
