1. Avant de commencer
Dans cet atelier de programmation, vous allez découvrir les convolutions et pourquoi elles sont si puissantes dans les scénarios de vision par ordinateur.
Dans l'atelier de programmation précédent, vous avez créé un réseau de neurones profond (DNN) simple pour la vision par ordinateur d'articles de mode. Cette règle était limitée, car elle exigeait que le vêtement soit le seul élément de l'image et qu'il soit centré.
Bien sûr, ce n'est pas un scénario réaliste. Vous devez faire en sorte que votre DNN soit capable d'identifier le vêtement sur des photos où il est entouré d'autres objets ou n'est pas placé au centre. Pour ce faire, vous devez utiliser des convolutions.
Prérequis
Cet atelier de programmation s'appuie sur le travail effectué dans deux ateliers précédents : Dites bonjour au "Hello, World" du machine learning et Créer un modèle de vision par ordinateur. Veuillez les effectuer avant de continuer.
Points abordés
- Que sont les convolutions ?
- Créer une carte des fonctionnalités
- Qu'est-ce que le regroupement ?
Objectifs de l'atelier
- Carte de caractéristiques d'une image
Prérequis
Vous trouverez le code du reste de l'atelier de programmation dans Colab.
Vous aurez également besoin de TensorFlow et des bibliothèques que vous avez installées dans l'atelier de programmation précédent.
2. Que sont les convolutions ?
Une convolution est un filtre qui passe sur une image, l'analyse et extrait les caractéristiques importantes.
Imaginons que vous ayez une image d'une personne portant des baskets. Comment détecteriez-vous la présence d'une basket dans l'image ? Pour que votre programme "voie" l'image comme une basket, vous devez extraire les caractéristiques importantes et flouter celles qui ne le sont pas. C'est ce qu'on appelle le mapping des caractéristiques.
Le processus de cartographie des fonctionnalités est théoriquement simple. Vous allez analyser chaque pixel de l'image, puis examiner ses pixels voisins. Vous multipliez les valeurs de ces pixels par les pondérations équivalentes dans un filtre.
Exemple :
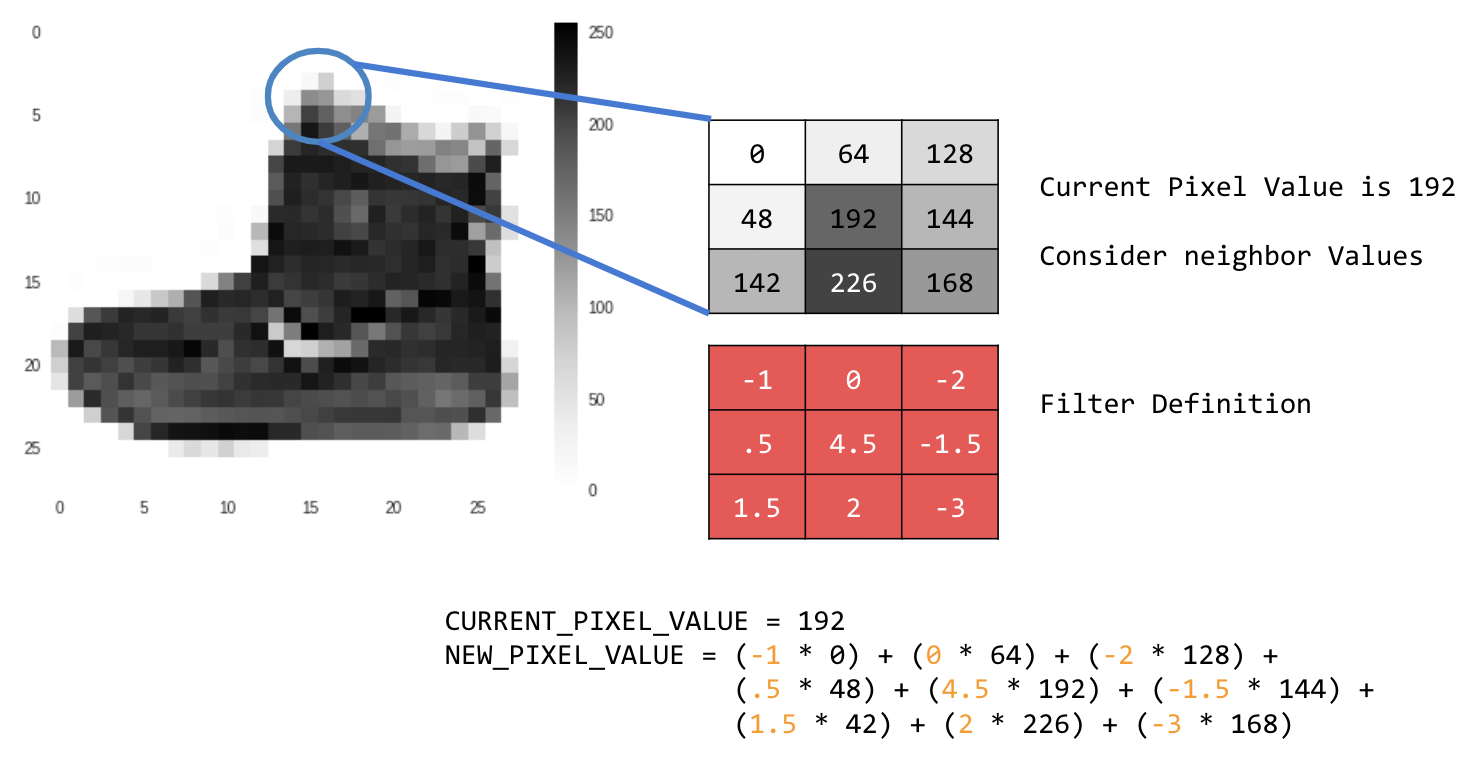
Dans ce cas, une matrice de convolution 3x3, ou noyau d'image, est spécifiée.
La valeur actuelle du pixel est de 192. Pour calculer la valeur du nouveau pixel, vous pouvez examiner les valeurs voisines, les multiplier par les valeurs spécifiées dans le filtre et définir la valeur du nouveau pixel sur le montant final.
Il est maintenant temps d'explorer le fonctionnement des convolutions en créant une convolution de base sur une image en niveaux de gris 2D.
Vous allez le démontrer avec l'image ascent de SciPy. Il s'agit d'une belle image intégrée avec de nombreux angles et lignes.
3. Commencer à coder
Commencez par importer des bibliothèques Python et l'image de l'ascension :
import cv2
import numpy as np
from scipy import misc
i = misc.ascent()
Ensuite, utilisez la bibliothèque Pyplot matplotlib pour dessiner l'image et savoir à quoi elle ressemble :
import matplotlib.pyplot as plt
plt.grid(False)
plt.gray()
plt.axis('off')
plt.imshow(i)
plt.show()

Vous pouvez voir qu'il s'agit d'une image d'une cage d'escalier. Vous pouvez essayer et isoler de nombreuses fonctionnalités. Par exemple, il y a des lignes verticales fortes.
L'image est stockée sous forme de tableau NumPy. Nous pouvons donc créer l'image transformée en copiant simplement ce tableau. Les variables size_x et size_y contiendront les dimensions de l'image afin que vous puissiez effectuer une boucle dessus ultérieurement.
i_transformed = np.copy(i)
size_x = i_transformed.shape[0]
size_y = i_transformed.shape[1]
4. Créer la matrice de convolution
Commencez par créer une matrice de convolution (ou noyau) sous la forme d'un tableau 3x3 :
# This filter detects edges nicely
# It creates a filter that only passes through sharp edges and straight lines.
# Experiment with different values for fun effects.
#filter = [ [0, 1, 0], [1, -4, 1], [0, 1, 0]]
# A couple more filters to try for fun!
filter = [ [-1, -2, -1], [0, 0, 0], [1, 2, 1]]
#filter = [ [-1, 0, 1], [-2, 0, 2], [-1, 0, 1]]
# If all the digits in the filter don't add up to 0 or 1, you
# should probably do a weight to get it to do so
# so, for example, if your weights are 1,1,1 1,2,1 1,1,1
# They add up to 10, so you would set a weight of .1 if you want to normalize them
weight = 1
Maintenant, calculez les pixels de sortie. Parcourez l'image en laissant une marge d'un pixel, puis multipliez chacun des voisins du pixel actuel par la valeur définie dans le filtre.
Cela signifie que le voisin actuel du pixel au-dessus et à gauche sera multiplié par l'élément en haut à gauche du filtre. Multipliez ensuite le résultat par le poids et assurez-vous qu'il est compris entre 0 et 255.
Enfin, chargez la nouvelle valeur dans l'image transformée :
for x in range(1,size_x-1):
for y in range(1,size_y-1):
output_pixel = 0.0
output_pixel = output_pixel + (i[x - 1, y-1] * filter[0][0])
output_pixel = output_pixel + (i[x, y-1] * filter[0][1])
output_pixel = output_pixel + (i[x + 1, y-1] * filter[0][2])
output_pixel = output_pixel + (i[x-1, y] * filter[1][0])
output_pixel = output_pixel + (i[x, y] * filter[1][1])
output_pixel = output_pixel + (i[x+1, y] * filter[1][2])
output_pixel = output_pixel + (i[x-1, y+1] * filter[2][0])
output_pixel = output_pixel + (i[x, y+1] * filter[2][1])
output_pixel = output_pixel + (i[x+1, y+1] * filter[2][2])
output_pixel = output_pixel * weight
if(output_pixel<0):
output_pixel=0
if(output_pixel>255):
output_pixel=255
i_transformed[x, y] = output_pixel
5. Examiner les résultats
Maintenant, représentez l'image pour voir l'effet du filtre :
# Plot the image. Note the size of the axes -- they are 512 by 512
plt.gray()
plt.grid(False)
plt.imshow(i_transformed)
#plt.axis('off')
plt.show()

Examinez les valeurs de filtre suivantes et leur impact sur l'image.
L'utilisation de [-1,0,1,-2,0,2,-1,0,1] donne un ensemble très fort de lignes verticales :
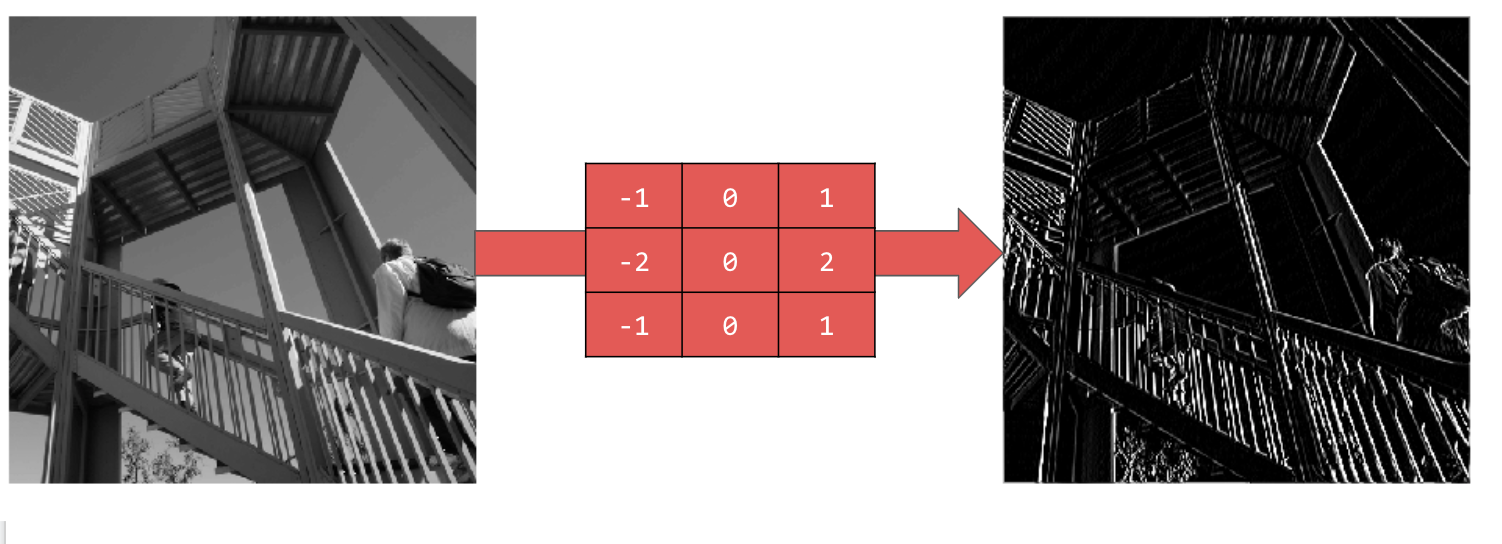
L'utilisation de [-1,-2,-1,0,0,0,1,2,1] donne des lignes horizontales :
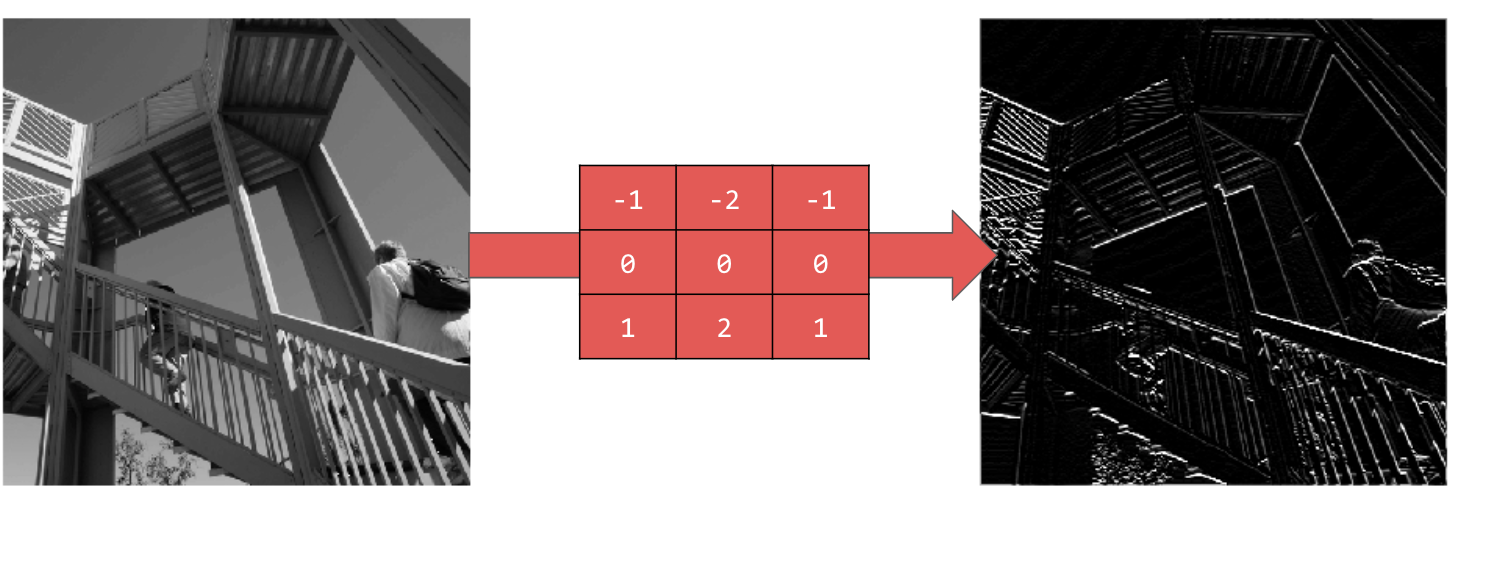
Explorez différentes valeurs ! Essayez également des filtres de différentes tailles, par exemple 5x5 ou 7x7.
6. Comprendre le pooling
Maintenant que vous avez identifié les caractéristiques essentielles de l'image, que devez-vous faire ? Comment utiliser la carte de caractéristiques obtenue pour classer les images ?
Comme les convolutions, le pooling aide considérablement à détecter les caractéristiques. Les couches de pooling réduisent la quantité globale d'informations dans une image tout en conservant les caractéristiques détectées.
Il existe différents types de mise en commun, mais vous utiliserez celui appelé "Pooling maximal".
Parcourez l'image et, à chaque point, examinez le pixel et ses voisins immédiats à droite, en dessous et en dessous à droite. Prenez la plus grande de ces valeurs (d'où le pooling max) et chargez-la dans la nouvelle image. La nouvelle image sera donc quatre fois plus petite que l'ancienne. 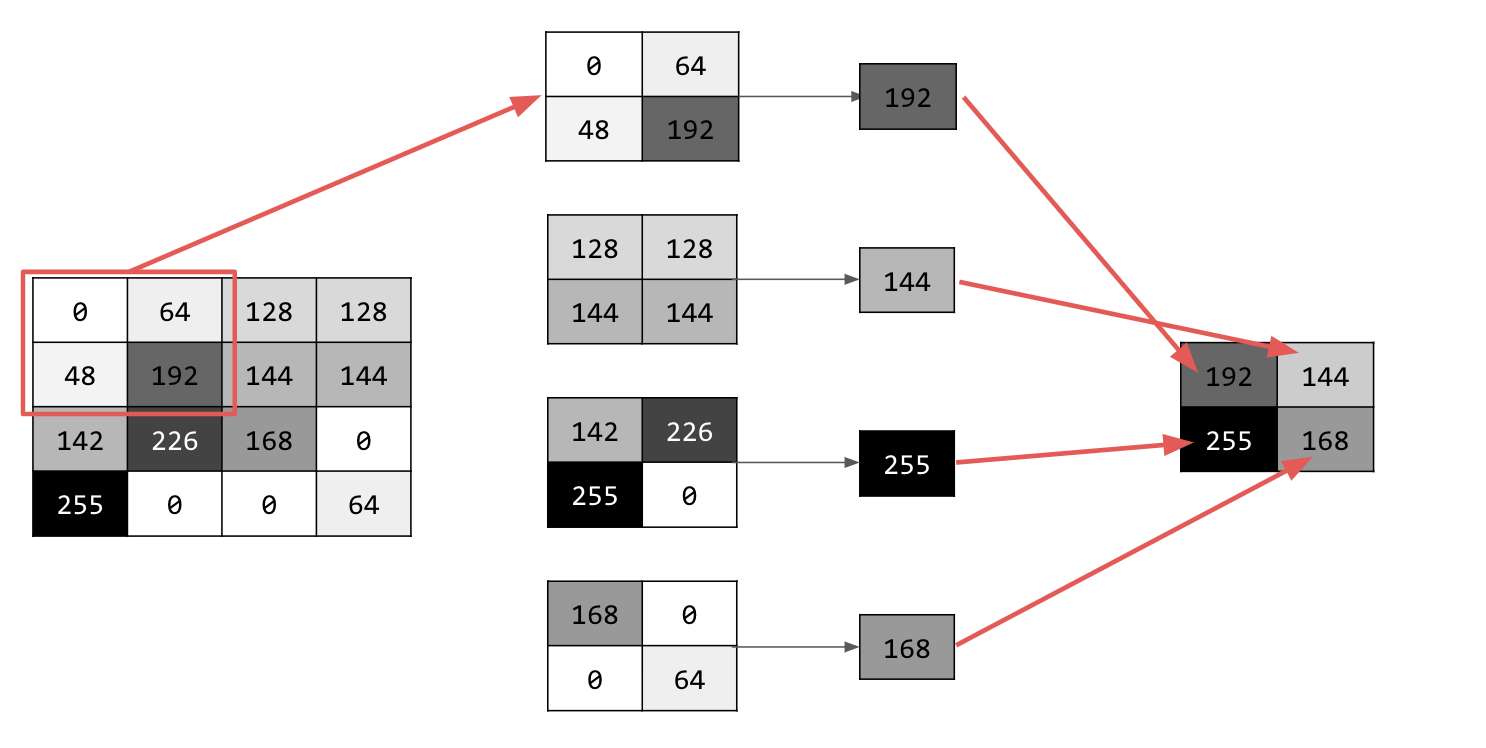
7. Écrire le code pour le pooling
Le code suivant affichera un pooling (2, 2). Exécutez-le pour voir le résultat.
Vous verrez que, bien que l'image soit quatre fois plus petite que l'originale, elle a conservé toutes ses caractéristiques.
new_x = int(size_x/2)
new_y = int(size_y/2)
newImage = np.zeros((new_x, new_y))
for x in range(0, size_x, 2):
for y in range(0, size_y, 2):
pixels = []
pixels.append(i_transformed[x, y])
pixels.append(i_transformed[x+1, y])
pixels.append(i_transformed[x, y+1])
pixels.append(i_transformed[x+1, y+1])
pixels.sort(reverse=True)
newImage[int(x/2),int(y/2)] = pixels[0]
# Plot the image. Note the size of the axes -- now 256 pixels instead of 512
plt.gray()
plt.grid(False)
plt.imshow(newImage)
#plt.axis('off')
plt.show()

Notez les axes de ce graphique. L'image est désormais en 256 x 256, soit un quart de sa taille d'origine, et les caractéristiques détectées ont été améliorées malgré la réduction de la quantité de données dans l'image.
8. Félicitations
Vous avez créé votre premier modèle de vision par ordinateur. Pour savoir comment améliorer vos modèles de vision par ordinateur, consultez Créer des réseaux de neurones convolutifs (CNN) pour améliorer la vision par ordinateur.
