Trang này được dịch bởi Cloud Translation API.

Các loại Tensor thưa thớt trong MLIR

Mã hoá tensor thưa thớt là một thuộc tính để mã hoá thông tin về tính chất hụt của tensor, được lấy cảm hứng bằng cách TACO hình thức hoá các tensor thưa thớt. Phương thức mã hoá này cuối cùng sẽ được sử dụng bằng cách truyền trình phân tích cú pháp để tự động tạo mã thưa thớt hoàn toàn từ một biểu diễn không phụ thuộc vào độ thưa của việc tính toán, tức là thưa thớt ngầm ẩn biểu diễn được chuyển đổi thành biểu diễn thưa rõ ràng, Các vòng lặp cùng lặp hoạt động trên bộ nhớ thưa thớt thay vì tensor có độ hẹp mã hoá. Trình biên dịch truyền đi trước lần truyền sparsifier này cần được biết ngữ nghĩa của các loại tensor có mã hoá độ thưa thớt như vậy.

Trong phương thức mã hoá này, chúng tôi sử dụng dimension để tham chiếu đến các trục của tensor ngữ nghĩa, và level để đề cập đến các trục của định dạng lưu trữ thực tế, tức là biểu diễn hoạt động của tensor thưa trong bộ nhớ. Số lượng kích thước thường giống với số lượng cấp (chẳng hạn như định dạng lưu trữ CSR). Tuy nhiên, quá trình mã hoá cũng có thể ánh xạ lên cấp cao hơn (ví dụ: để mã hoá định dạng lưu trữ BSR có khối thưa thớt) hoặc thành các cấp bậc thấp hơn (ví dụ: để tuyến tính hoá kích thước thành một cấp duy nhất trong bộ nhớ).

Mã hoá chứa một bản đồ cung cấp các thông tin sau:

Một trình tự theo thứ tự liên quan đến các thông số kỹ thuật về phương diện, trong đó mỗi thông số sẽ xác định:
- kích thước chiều (ngầm ẩn từ hình dạng kích thước của tensor)
- một biểu thức phương diện
Một trình tự theo thứ tự liên quan đến các thông số của cấp, trong đó mỗi thông số bao gồm thông số kỹ thuật bắt buộc level-type, xác định cách lưu trữ cấp. Mỗi loại cấp độ bao gồm:
- một biểu thức cấp độ, xác định thông tin được lưu trữ
- định dạng cấp độ
- tập hợp các thuộc tính cấp áp dụng cho định dạng cấp

Mỗi biểu thức mức là một biểu thức affine thay vì các biến thứ nguyên. Do đó, biểu thức mức xác định chung một bản đồ affine từ toạ độ kích thước đến toạ độ theo cấp. Biểu thức phương diện định nghĩa chung bản đồ nghịch đảo, thông tin này chỉ cần được cung cấp cho các trường hợp chi tiết mà không thể suy luận được tự động.

Mỗi phương diện cũng có thể có một SparseTensorDimSliceAttr không bắt buộc. Trong định dạng lưu trữ thưa thớt, chúng tôi đề cập đến chỉ mục được lưu trữ rõ ràng làm tọa độ và bù trừ vào định dạng lưu trữ dưới dạng vị trí.

Sau đây là các định dạng cấp độ được hỗ trợ:

dense : tất cả các mục cùng với cấp độ này đều được lưu trữ
nén : chỉ các giá trị khác 0 ở cấp độ này mới được lưu trữ
loose_compressed : dưới dạng nén, nhưng sẽ tạo không gian trống giữa các khu vực
singleton : một biến thể của định dạng nén, trong đó toạ độ không có các phiên bản đồng cấp
block2_4 : quá trình nén sử dụng phương thức mã hoá 2:4 cho mỗi khối 1x4

Đối với cấp độ nén, mỗi khoảng thời gian vị trí được biểu thị bằng một bản thu gọn có giới hạn dưới là pos(i) và pos(i+1) - 1 cận trên, ngụ ý rằng các khoảng thời gian liên tiếp phải xuất hiện theo thứ tự mà không có bất kỳ "lỗ hổng" nào ở giữa chúng. Định dạng nén rời giúp giảm bớt những hạn chế này bằng cách biểu thị mỗi khoảng vị trí bằng lo(i) giới hạn dưới và hi(i) giới hạn trên. cho phép các khoảng thời gian xuất hiện theo thứ tự tuỳ ý và có khoảng trống giữa chúng.

Theo mặc định, mỗi loại cấp có đặc điểm là duy nhất (không trùng lặp toạ độ ở cấp độ đó) và được sắp xếp theo thứ tự (các toạ độ xuất hiện được sắp xếp theo cấp độ). Bạn có thể thêm các thuộc tính sau vào một định dạng cấp để thay đổi hành vi mặc định này:

không duy nhất : các toạ độ trùng lặp có thể xuất hiện ở cấp này
không theo thứ tự : các toạ độ có thể xuất hiện theo thứ tự tham số

Ngoài bản đồ, hai trường sau đây là tuỳ chọn:

Chiều rộng bit bắt buộc để lưu trữ vị trí (độ lệch tích phân) vào lược đồ lưu trữ thưa thớt). Chiều rộng hẹp làm giảm bộ nhớ diện tích lưu trữ trên đầu, miễn là chiều rộng vừa đủ để xác định tổng phạm vi yêu cầu (ví dụ: số lượng dữ liệu được lưu trữ tối đa mục nhập ở tất cả các cấp gián tiếp). Các lựa chọn là 8, 16, 32, 64 hoặc giá trị mặc định 0 để biểu thị chiều rộng bit gốc.
Chiều rộng bit bắt buộc để lưu trữ toạ độ (các toạ độ của mục nhập đã lưu). Chiều rộng hẹp giúp giảm mức sử dụng bộ nhớ cho bộ nhớ trên cao, miễn là chiều rộng đủ để xác định tổng phạm vi yêu cầu (ví dụ: giá trị lớn nhất của mỗi tensor phối hợp ở tất cả các cấp). Các lựa chọn là 8, 16, 32, 64 hoặc 0 theo mặc định để biểu thị chiều rộng bit gốc.

Ví dụ

Ở định dạng CSR(Compressed Sparse Row) như trình bày dưới đây, mã hoá tensor thưa thớt sẽ là:

#CSR = #sparse_tensor.encoding<{
  map = (i, j) -> (i : dense, j : compressed)
}>

Nó cho biết first dimension (hàng) ánh xạ tới first level, là cấp dense, được biểu thị bằng kích thước 4. Và second dimension (cột) ánh xạ tới second level, được biểu thị bằng mảng vị trí và mảng toạ độ. Giá trị 3 ([1, 1] trong ma trận ban đầu) là được biểu thị bằng độ lệch của mảng vị trí (số hàng của giá trị 3 là 1 trong ma trận ban đầu vì đó là cặp bù thứ hai và số cột nằm ở chỉ mục [2 : 4) trong mảng toạ độ). Và trong chúng ta có thể thấy rằng số cột của 3 là 1 trong ma trận gốc.

Đối với định dạng BSR(Block Sparse Row), loại tensor thưa thớt là:

#BSR = #sparse_tensor.encoding<{
  map = (i, j) ->
    ( i floordiv 2 : dense
    , j floordiv 2 : compressed
    , i mod 2 : dense
    , j mod 2 : dense
    )

Hãy xem xét ma trận thưa sau, với các khối 2x2:

Example 2x2 block storage:
 +-----+-----+-----+    +-----+-----+-----+
 | 1 2 | . . | 4 . |    | 1 2 |     | 4 0 |
 | . 3 | . . | . 5 |    | 0 3 |     | 0 5 |
 +-----+-----+-----+ => +-----+-----+-----+
 | . . | 6 7 | . . |    |     | 6 7 |     |
 | . . | 8 . | . . |    |     | 8 0 |     |
 +-----+-----+-----+    +-----+-----+-----+

cuối cùng sẽ được lưu trữ ở định dạng có hương vị TACO như

Stored as:
   positions[1]   : 0 2 3
   coordinates[1] : 0 2 1
   values         : 1.000000 2.000000 0.000000 3.000000
                    4.000000 0.000000 0.000000 5.000000
                    6.000000 7.000000 8.000000 0.000000

Thật tình cờ, đây thực sự là Định dạng khối NVidia được trình bày trong tài liệu về cuSparse.

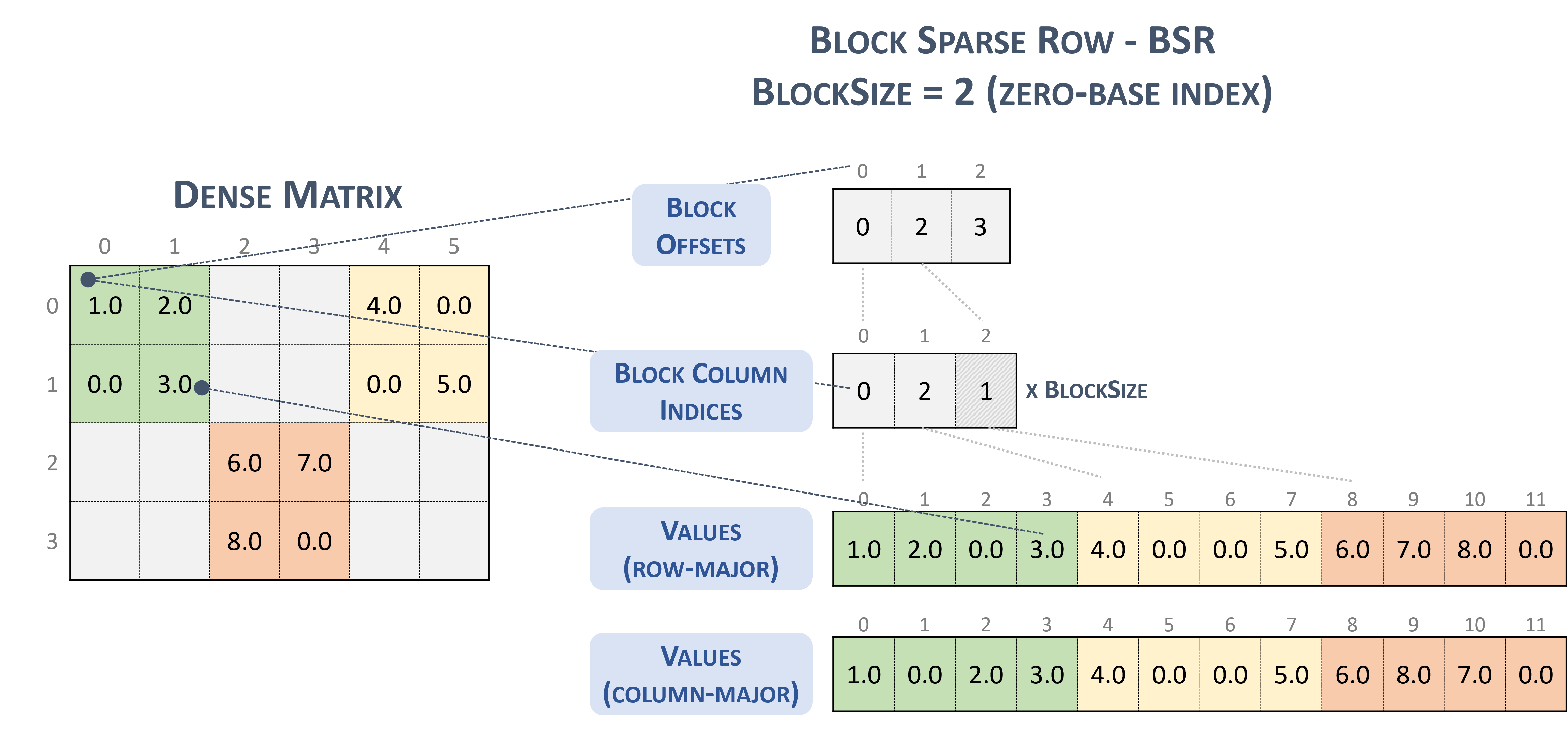
Chặn hàng thưa thớt. (n.d.-b). Nvidia. https://docs.nvidia.com/cuda/cusparse/_images/bsr.png

Chúng tôi cũng hỗ trợ Nvidia's 2:4 structured sparsity.

Sau đây là kiểu tensor thưa thớt cho trường hợp này:

#NV_24 = #sparse_tensor.encoding<{
  map = ( i, j ) -> ( i            : dense,
                      j floordiv 4 : dense,
                      j mod 4      : block2_4),
  crdWidth = 2  // 2-bits for each coordinate
}>

Cho ma trận mẫu được nêu trong tài liệu của NVidia:

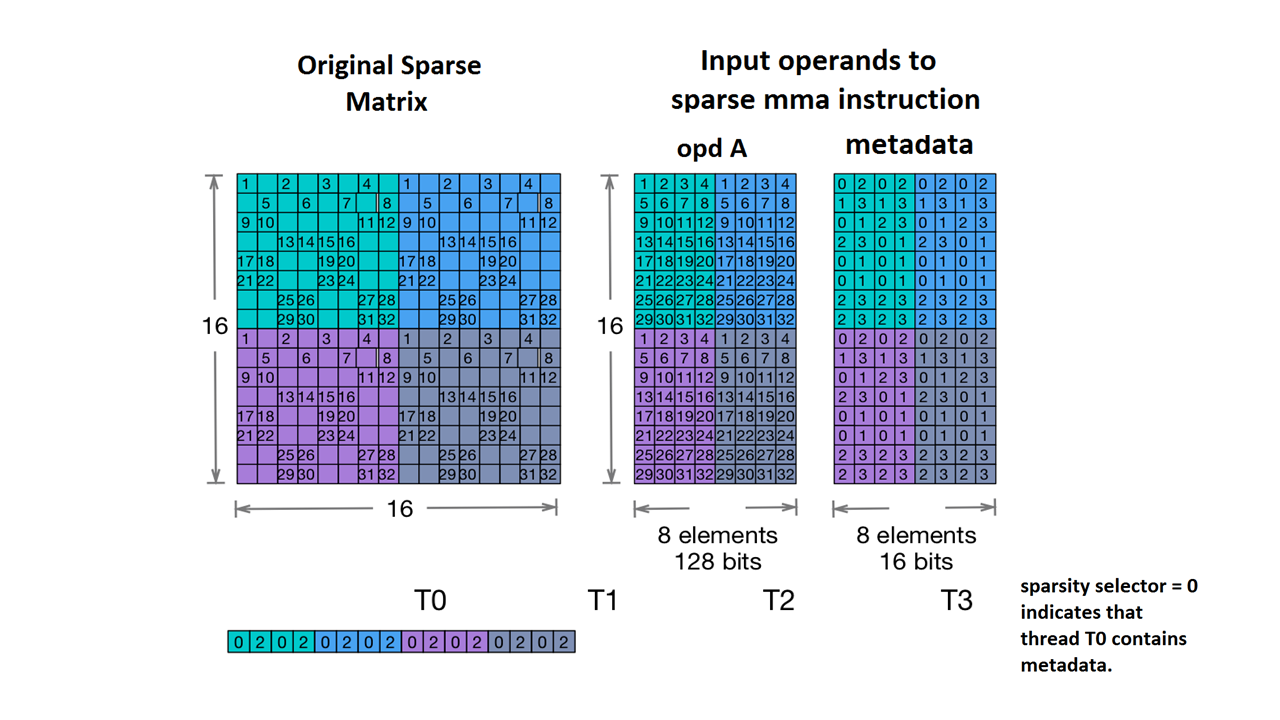
Ví dụ về bộ nhớ MMA thưa thớt. (n.d.). Nvidia. https://docs.nvidia.com/cuda/parallel-thread-execution/index.html#warp-level-matrix-instructions-for-sparse-mma

Giờ đây, MLIR sẽ ánh xạ ma trận này theo một bố cục giống hệt:

coordinates[2]  :
   0 2 0 2 0 2 0 2
   1 3 1 3 1 3 1 3
   0 1 2 3 0 1 2 3
   2 3 0 1 2 3 0 1
   0 1 0 1 0 1 0 1
   0 1 0 1 0 1 0 1
   2 3 2 3 2 3 2 3
   2 3 2 3 2 3 2 3
   0 2 0 2 0 2 0 2
   1 3 1 3 1 3 1 3
   0 1 2 3 0 1 2 3
   2 3 0 1 2 3 0 1
   0 1 0 1 0 1 0 1
   0 1 0 1 0 1 0 1
   2 3 2 3 2 3 2 3
   2 3 2 3 2 3 2 3
values :
  1.000000 2.000000 3.000000 4.000000 1.000000 2.000000 3.000000 4.000000
  5.000000 6.000000 7.000000 8.000000 5.000000 6.000000 7.000000 8.000000
  9.000000 10.000000 11.000000 12.000000 9.000000 10.000000 11.000000 12.000000
  13.000000 14.000000 15.000000 16.000000 13.000000 14.000000 15.000000 16.000000
  17.000000 18.000000 19.000000 20.000000 17.000000 18.000000 19.000000 20.000000
  21.000000 22.000000 23.000000 24.000000 21.000000 22.000000 23.000000 24.000000
  25.000000 26.000000 27.000000 28.000000 25.000000 26.000000 27.000000 28.000000
  29.000000 30.000000 31.000000 32.000000 29.000000 30.000000 31.000000 32.000000
  1.000000 2.000000 3.000000 4.000000 1.000000 2.000000 3.000000 4.000000
  5.000000 6.000000 7.000000 8.000000 5.000000 6.000000 7.000000 8.000000
  9.000000 10.000000 11.000000 12.000000 9.000000 10.000000 11.000000 12.000000
  13.000000 14.000000 15.000000 16.000000 13.000000 14.000000 15.000000 16.000000
  17.000000 18.000000 19.000000 20.000000 17.000000 18.000000 19.000000 20.000000
  21.000000 22.000000 23.000000 24.000000 21.000000 22.000000 23.000000 24.000000
  25.000000 26.000000 27.000000 28.000000 25.000000 26.000000 27.000000 28.000000
  29.000000 30.000000 31.000000 32.000000 29.000000 30.000000 31.000000 32.000000

Ví dụ khác:

// Sparse vector.
#SparseVector = #sparse_tensor.encoding<{
  map = (i) -> (i : compressed)
}>
... tensor<?xf32, #SparseVector> ...

// Sorted coordinate scheme.
#SortedCOO = #sparse_tensor.encoding<{
  map = (i, j) -> (i : compressed(nonunique), j : singleton)
}>
... tensor<?x?xf64, #SortedCOO> ...

// Batched sorted coordinate scheme, with high encoding.
#BCOO = #sparse_tensor.encoding<{
  map = (i, j, k) -> (i : dense, j : compressed(nonunique, high), k : singleton)
}>
... tensor<10x10xf32, #BCOO> ...

// Compressed sparse row.
#CSR = #sparse_tensor.encoding<{
  map = (i, j) -> (i : dense, j : compressed)
}>
... tensor<100x100xbf16, #CSR> ...

// Doubly compressed sparse column storage with specific bitwidths.
#DCSC = #sparse_tensor.encoding<{
  map = (i, j) -> (j : compressed, i : compressed),
  posWidth = 32,
  crdWidth = 8
}>
... tensor<8x8xf64, #DCSC> ...

// Block sparse row storage (2x3 blocks).
#BSR = #sparse_tensor.encoding<{
  map = ( i, j ) ->
  ( i floordiv 2 : dense,
    j floordiv 3 : compressed,
    i mod 2      : dense,
    j mod 3      : dense
  )
}>
... tensor<20x30xf32, #BSR> ...

// Same block sparse row storage (2x3 blocks) but this time
// also with a redundant reverse mapping, which can be inferred.
#BSR_explicit = #sparse_tensor.encoding<{
  map = { ib, jb, ii, jj }
        ( i = ib * 2 + ii,
          j = jb * 3 + jj) ->
  ( ib = i floordiv 2 : dense,
    jb = j floordiv 3 : compressed,
    ii = i mod 2 : dense,
    jj = j mod 3 : dense)
}>
... tensor<20x30xf32, #BSR_explicit> ...

// ELL format.
// In the simple format for matrix, one array stores values and another
// array stores column indices. The arrays have the same number of rows
// as the original matrix, but only have as many columns as
// the maximum number of nonzeros on a row of the original matrix.
// There are many variants for ELL such as jagged diagonal scheme.
// To implement ELL, map provides a notion of "counting a
// dimension", where every stored element with the same coordinate
// is mapped to a new slice. For instance, ELL storage of a 2-d
// tensor can be defined with the mapping (i, j) -> (#i, i, j)
// using the notation of [Chou20]. Lacking the # symbol in MLIR's
// affine mapping, we use a free symbol c to define such counting,
// together with a constant that denotes the number of resulting
// slices. For example, the mapping [c](i, j) -> (c * 3 * i, i, j)
// with the level-types ["dense", "dense", "compressed"] denotes ELL
// storage with three jagged diagonals that count the dimension i.
#ELL = #sparse_tensor.encoding<{
  map = [c](i, j) -> (c * 3 * i : dense, i : dense, j : compressed)
}>
... tensor<?x?xf64, #ELL> ...

// CSR slice (offset = 0, size = 4, stride = 1 on the first dimension;
// offset = 0, size = 8, and a dynamic stride on the second dimension).
#CSR_SLICE = #sparse_tensor.encoding<{
  map = (i : #sparse_tensor<slice(0, 4, 1)>,
          j : #sparse_tensor<slice(0, 8, ?)>) ->
        (i : dense, j : compressed)
}>
... tensor<?x?xf64, #CSR_SLICE> ...

Các loại Tensor thưa thớt trong MLIR Sử dụng bộ sưu tập để sắp xếp ngăn nắp các trang Lưu và phân loại nội dung dựa trên lựa chọn ưu tiên của bạn.

Ví dụ

Các loại Tensor thưa thớt trong MLIR