Ta strona została przetłumaczona przez Cloud Translation API.

Rozproszone typy Tensor w MLIR

Kodowanie tensorów rozproszonych to atrybut służący do kodowania informacji na własności rozproszenia tensorów, inspirowane przez formalizację tensorów rozproszonych przez TACO. To kodowanie jest ostatecznie używane za pomocą karty sparsifier, aby w pełni automatycznie wygenerować rozproszony kod z niewymagająca od rozproszenia reprezentacja obliczeń, tj. niejawna rozproszona jest przekształcana na wyraźną rozproszoną reprezentację, gdzie pętle współiteracji działają na rozproszonej pamięci masowej w postaci formatów, a nie tensorów o małej ilości kodowanie. Musisz wiedzieć, które karty w kompilatorze uruchamiane przed tym karnetem sparatora semantyki typów tensorów o tak rzadkim kodowaniu.

W tym kodowaniu używamy wymiaru dimension, aby to osie tensora semantycznego, i level w odniesieniu do osi rzeczywistego formatu pamięci masowej, czyli operacyjna reprezentacja tensora rozproszonego w pamięci. Liczba są zwykle takie same liczbę poziomów (np. format przechowywania danych CSR). Jednak kodowanie może też mapować z wymiarów wyższego rzędu na wyższym poziomie (np. do zakodowania rozproszonego blokowego formatu pamięci BSR) lub do zakodowania niższego rzędu (aby na przykład liniować wymiary jako pojedynczy poziom miejsca na dane).

Kodowanie zawiera mapę, która zapewnia:

Uporządkowana sekwencja specyfikacji wymiarów, z których każda określa:
- rozmiar-wymiar (domyślnie na podstawie kształtu tensora)
- wyrażenie wymiaru
Uporządkowana sekwencja specyfikacji poziomów, z których każdy zawiera wymagany element level-type, który określa sposób przechowywania poziomu. Każdy rodzaj składa się z:
- wyrażenie poziomu, które określa, co jest zapisywane
- format poziomu,
- zbiór właściwości poziomu, które mają zastosowanie do formatu poziomu

Każde wyrażenie poziomu jest wyrażeniem afinicznym niż zmienne wymiarów. Dlatego wyrażenia poziomów łącznie definiują mapa afinacyjna ze współrzędnych wymiaru do i współrzędnych. Wyrażenia wymiarów razem definiują odwrotną mapę, który należy podać tylko w bardziej złożonych przypadkach, w których nie można tego wywnioskować. automatycznie.

Każdy wymiar może też mieć opcjonalny SparseTensorDimSliceAttr. W przypadku formatu rozproszonego pamięci masowej powołujemy się na indeksy przechowywane w sposób jawny. jako współrzędne i odsunięcia na format pamięci masowej jako pozycje.

Obsługiwane są te formaty:

gęste : zapisywane są wszystkie wpisy na tym poziomie,
skompresowany : przechowywane są tylko liczby inne niż zero na tym poziomie.
loose_compressed : jako skompresowany, ale pozwala na zwolnienie przestrzeni między regionami
singleton : wariant formatu skompresowanego, w którym współrzędne nie mają elementów potomnych.
block2_4 : kompresja korzysta z kodowania 2:4 na blok 1x4.

W przypadku poziomu skompresowanego każdy przedział pozycji jest przedstawiany w z dolną granicą pos(i) i górną z wartością pos(i+1) - 1, co oznacza że kolejne interwały muszą występować w kolejności, bez żadnych „dziur” między znakami alfanumerycznymi . Luźno skompresowany format łagodzi te ograniczenia, reprezentując każdy interwał pozycji z dolną granicą lo(i) i górną granicą hi(i), która Dzięki temu interwały mogą pojawiać się w dowolnej kolejności, a między łokciami jest przestrzeń między łokciami.

Domyślnie każdy typ poziomu jest niepowtarzalny (nie powtarza się współrzędnych na tym poziomie) i uporządkowane (współrzędne są posortowane ). Poniższe właściwości można dodać do formatu poziomu, aby zmienić: to domyślne zachowanie:

nonunikalny : na poziomie danego poziomu mogą pojawić się zduplikowane współrzędne.
nonorder (niezarządzone): współrzędne mogą być ułożone według nakazu urzędu.

Oprócz mapy opcjonalne są też te 2 pola:

Wymagana przepustowość bitowa do przechowywania pozycji (przesunięcia całkowite) do schematu rozproszonego pamięci masowej). Mała szerokość zmniejsza ilość pamięci jaka pojemność pamięci masowej, o ile szerokość wystarczy zdefiniować całkowity wymagany zakres (np. maksymalną liczbę przechowywanych wpisów na wszystkich poziomach pośrednich). Dostępne opcje to 8, 16, 32, 64 lub domyślnie 0, aby wskazać natywną przepustowość.
Wymagana szerokość bitów na potrzeby przechowywania współrzędnych (współrzędne) zapisanych wpisów). Mała szerokość zmniejsza wykorzystanie pamięci nad pamięcią masową, jeśli tylko szerokość wystarcza do zdefiniowania całkowity wymagany zakres (tzn. maksymalna wartość każdego tensora) na wszystkich poziomach). Dostępne opcje to 8, 16, 32, 64 lub (domyślnie) 0, aby wskazać natywną szerokość bitów.

Przykłady

W formacie CSR(Compressed Sparse Row) jak widać poniżej, kodowanie rozproszonego tensora będzie wyglądać tak:

#CSR = #sparse_tensor.encoding<{
  map = (i, j) -> (i : dense, j : compressed)
}>

Wskazuje on, że wiersz first dimension (wiersz) jest mapowany na first level, czyli poziom dense, który wskazuje rozmiar 4. oraz second dimension (kolumna) mapuje się na element second level, wskazywany przez tablicę pozycji i tablicę współrzędnych. Wartość 3 ([1, 1] w pierwotnej macierzy) to reprezentowany przez przesunięcie względem tablicy pozycji (numer wiersza wartości 3) jest 1 w oryginalnej macierzy, ponieważ jest to druga para przesunięcia, a jej numer kolumny znajduje się w indeksie [2 : 4) w tablicy współrzędnych). W w tablicy współrzędnych, zobaczymy, że wartość kolumny 3 ma wartość 1 oryginalnej macierzy.

W formacie BSR(Block Sparse Row) typ tensora rozproszonego to:

#BSR = #sparse_tensor.encoding<{
  map = (i, j) ->
    ( i floordiv 2 : dense
    , j floordiv 2 : compressed
    , i mod 2 : dense
    , j mod 2 : dense
    )

Rozważmy następującą macierz rozproszoną zawierającą bloki 2 x 2:

Example 2x2 block storage:
 +-----+-----+-----+    +-----+-----+-----+
 | 1 2 | . . | 4 . |    | 1 2 |     | 4 0 |
 | . 3 | . . | . 5 |    | 0 3 |     | 0 5 |
 +-----+-----+-----+ => +-----+-----+-----+
 | . . | 6 7 | . . |    |     | 6 7 |     |
 | . . | 8 . | . . |    |     | 8 0 |     |
 +-----+-----+-----+    +-----+-----+-----+

który jest ostatecznie przechowywany w formacie smakowym TACO,

Stored as:
   positions[1]   : 0 2 3
   coordinates[1] : 0 2 1
   values         : 1.000000 2.000000 0.000000 3.000000
                    4.000000 0.000000 0.000000 5.000000
                    6.000000 7.000000 8.000000 0.000000

Co jest przypadkowe, dosłownie Format blokowy NVidia przedstawiony w dokumentacji cuSparse.

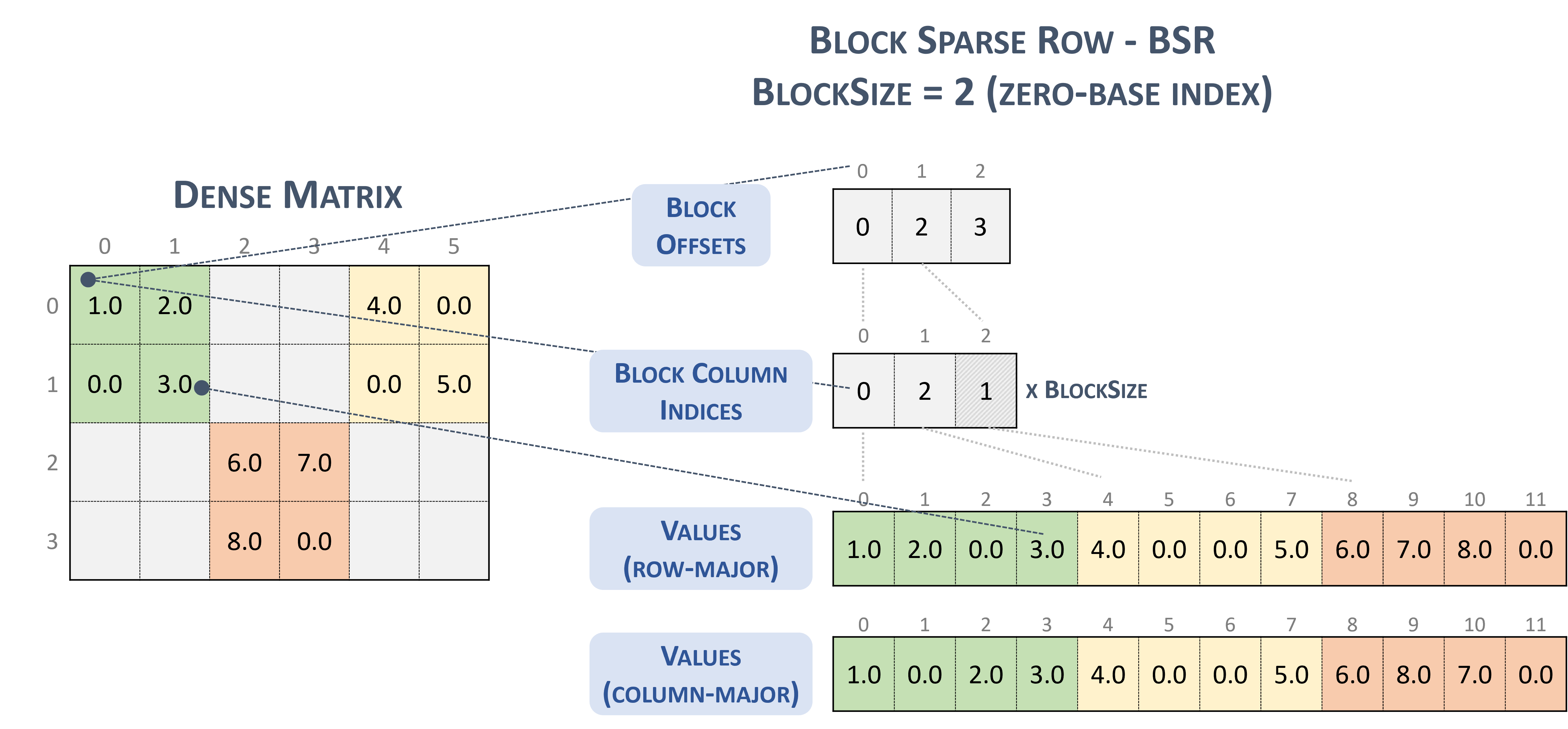
Zablokuj rozproszony wiersz. (b.d.–b). Nvidia https://docs.nvidia.com/cuda/cusparse/_images/bsr.png

Obsługujemy też Nvidia's 2:4 structured sparsity.

Typ tensora rozproszonego jest następujący:

#NV_24 = #sparse_tensor.encoding<{
  map = ( i, j ) -> ( i            : dense,
                      j floordiv 4 : dense,
                      j mod 4      : block2_4),
  crdWidth = 2  // 2-bits for each coordinate
}>

Biorąc pod uwagę macierz próbek podaną w dokumentacji NVidia:

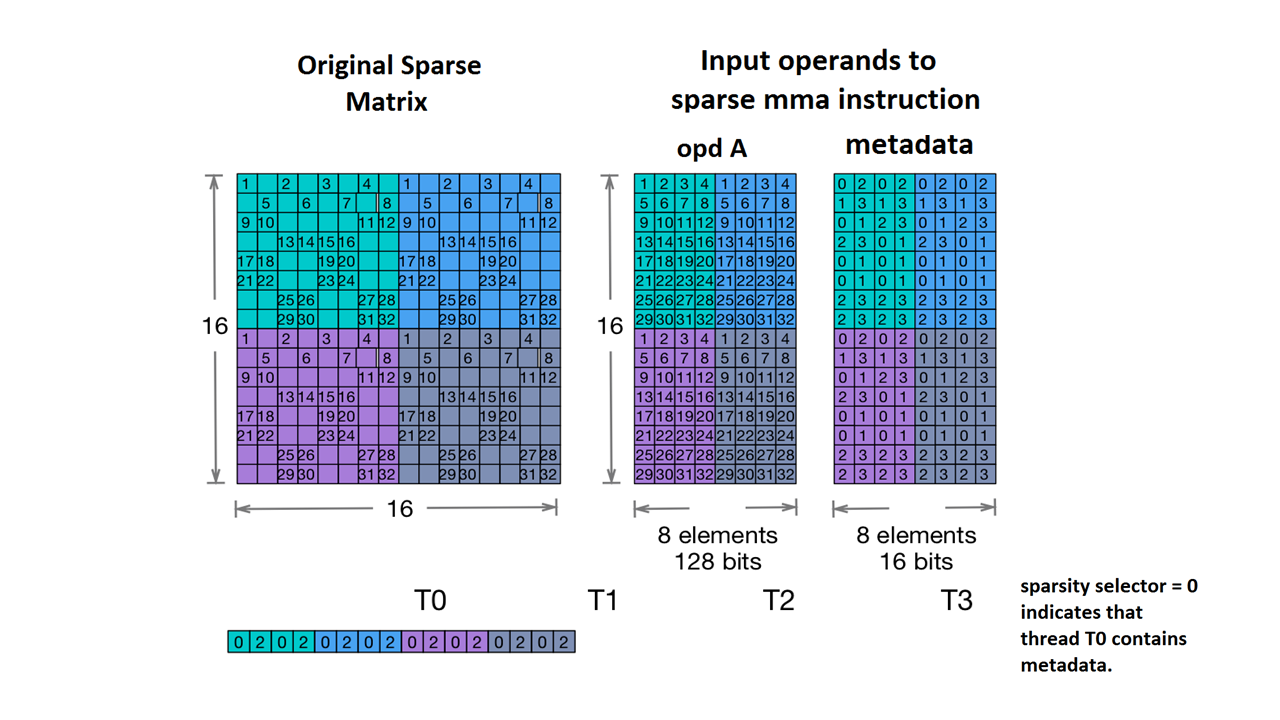
Przykład małej ilości miejsca na dane do MMA (brak danych). Nvidia https://docs.nvidia.com/cuda/parallel-thread-execution/index.html#warp-level-matrix-instructions-for-sparse-mma

MLIR mapuje teraz tę macierz na identyczny układ:

coordinates[2]  :
   0 2 0 2 0 2 0 2
   1 3 1 3 1 3 1 3
   0 1 2 3 0 1 2 3
   2 3 0 1 2 3 0 1
   0 1 0 1 0 1 0 1
   0 1 0 1 0 1 0 1
   2 3 2 3 2 3 2 3
   2 3 2 3 2 3 2 3
   0 2 0 2 0 2 0 2
   1 3 1 3 1 3 1 3
   0 1 2 3 0 1 2 3
   2 3 0 1 2 3 0 1
   0 1 0 1 0 1 0 1
   0 1 0 1 0 1 0 1
   2 3 2 3 2 3 2 3
   2 3 2 3 2 3 2 3
values :
  1.000000 2.000000 3.000000 4.000000 1.000000 2.000000 3.000000 4.000000
  5.000000 6.000000 7.000000 8.000000 5.000000 6.000000 7.000000 8.000000
  9.000000 10.000000 11.000000 12.000000 9.000000 10.000000 11.000000 12.000000
  13.000000 14.000000 15.000000 16.000000 13.000000 14.000000 15.000000 16.000000
  17.000000 18.000000 19.000000 20.000000 17.000000 18.000000 19.000000 20.000000
  21.000000 22.000000 23.000000 24.000000 21.000000 22.000000 23.000000 24.000000
  25.000000 26.000000 27.000000 28.000000 25.000000 26.000000 27.000000 28.000000
  29.000000 30.000000 31.000000 32.000000 29.000000 30.000000 31.000000 32.000000
  1.000000 2.000000 3.000000 4.000000 1.000000 2.000000 3.000000 4.000000
  5.000000 6.000000 7.000000 8.000000 5.000000 6.000000 7.000000 8.000000
  9.000000 10.000000 11.000000 12.000000 9.000000 10.000000 11.000000 12.000000
  13.000000 14.000000 15.000000 16.000000 13.000000 14.000000 15.000000 16.000000
  17.000000 18.000000 19.000000 20.000000 17.000000 18.000000 19.000000 20.000000
  21.000000 22.000000 23.000000 24.000000 21.000000 22.000000 23.000000 24.000000
  25.000000 26.000000 27.000000 28.000000 25.000000 26.000000 27.000000 28.000000
  29.000000 30.000000 31.000000 32.000000 29.000000 30.000000 31.000000 32.000000

Więcej przykładów:

// Sparse vector.
#SparseVector = #sparse_tensor.encoding<{
  map = (i) -> (i : compressed)
}>
... tensor<?xf32, #SparseVector> ...

// Sorted coordinate scheme.
#SortedCOO = #sparse_tensor.encoding<{
  map = (i, j) -> (i : compressed(nonunique), j : singleton)
}>
... tensor<?x?xf64, #SortedCOO> ...

// Batched sorted coordinate scheme, with high encoding.
#BCOO = #sparse_tensor.encoding<{
  map = (i, j, k) -> (i : dense, j : compressed(nonunique, high), k : singleton)
}>
... tensor<10x10xf32, #BCOO> ...

// Compressed sparse row.
#CSR = #sparse_tensor.encoding<{
  map = (i, j) -> (i : dense, j : compressed)
}>
... tensor<100x100xbf16, #CSR> ...

// Doubly compressed sparse column storage with specific bitwidths.
#DCSC = #sparse_tensor.encoding<{
  map = (i, j) -> (j : compressed, i : compressed),
  posWidth = 32,
  crdWidth = 8
}>
... tensor<8x8xf64, #DCSC> ...

// Block sparse row storage (2x3 blocks).
#BSR = #sparse_tensor.encoding<{
  map = ( i, j ) ->
  ( i floordiv 2 : dense,
    j floordiv 3 : compressed,
    i mod 2      : dense,
    j mod 3      : dense
  )
}>
... tensor<20x30xf32, #BSR> ...

// Same block sparse row storage (2x3 blocks) but this time
// also with a redundant reverse mapping, which can be inferred.
#BSR_explicit = #sparse_tensor.encoding<{
  map = { ib, jb, ii, jj }
        ( i = ib * 2 + ii,
          j = jb * 3 + jj) ->
  ( ib = i floordiv 2 : dense,
    jb = j floordiv 3 : compressed,
    ii = i mod 2 : dense,
    jj = j mod 3 : dense)
}>
... tensor<20x30xf32, #BSR_explicit> ...

// ELL format.
// In the simple format for matrix, one array stores values and another
// array stores column indices. The arrays have the same number of rows
// as the original matrix, but only have as many columns as
// the maximum number of nonzeros on a row of the original matrix.
// There are many variants for ELL such as jagged diagonal scheme.
// To implement ELL, map provides a notion of "counting a
// dimension", where every stored element with the same coordinate
// is mapped to a new slice. For instance, ELL storage of a 2-d
// tensor can be defined with the mapping (i, j) -> (#i, i, j)
// using the notation of [Chou20]. Lacking the # symbol in MLIR's
// affine mapping, we use a free symbol c to define such counting,
// together with a constant that denotes the number of resulting
// slices. For example, the mapping [c](i, j) -> (c * 3 * i, i, j)
// with the level-types ["dense", "dense", "compressed"] denotes ELL
// storage with three jagged diagonals that count the dimension i.
#ELL = #sparse_tensor.encoding<{
  map = [c](i, j) -> (c * 3 * i : dense, i : dense, j : compressed)
}>
... tensor<?x?xf64, #ELL> ...

// CSR slice (offset = 0, size = 4, stride = 1 on the first dimension;
// offset = 0, size = 8, and a dynamic stride on the second dimension).
#CSR_SLICE = #sparse_tensor.encoding<{
  map = (i : #sparse_tensor<slice(0, 4, 1)>,
          j : #sparse_tensor<slice(0, 8, ?)>) ->
        (i : dense, j : compressed)
}>
... tensor<?x?xf64, #CSR_SLICE> ...

Rozproszone typy Tensor w MLIR Zadbaj o dobrą organizację dzięki kolekcji Zapisuj i kategoryzuj treści zgodnie ze swoimi preferencjami.

Przykłady

Rozproszone typy Tensor w MLIR