Se usó la API de Cloud Translation para traducir esta página.

Tipos de tensores dispersos en MLIR

La codificación de tensor dispersa es un atributo para codificar información sobre las propiedades de dispersión de los tensores, inspiradas por la formalización TACO de tensores dispersos. Con el tiempo, esta codificación se usa mediante un pase de sparsifier para generar código disperso de forma completa y automática a partir de un representación agnóstica del cálculo agnóstica, es decir, una dispersión implícita se convierte en una representación dispersa explícita en la que bucles de coiteración operan en almacenamiento disperso en lugar de tensores con dispersión o la codificación. Los pases de compilador que se ejecutan antes de que este pase de espaciado deben conocerse de la semántica de los tipos de tensores con una codificación de dispersión.

En esta codificación, usamos la dimensión para se refieren a los ejes del tensor semántico, y level para hacer referencia a los ejes del formato de almacenamiento real, es decir, el operativa del tensor disperso en la memoria. El número de dimensiones es generalmente lo mismo que la cantidad de niveles (como el formato de almacenamiento de CSR) Sin embargo, la codificación también puede asignar dimensiones a niveles de orden superior (por ejemplo, para codificar un formato de almacenamiento BSR disperso en bloques) o a niveles de orden inferior (por ejemplo, para linealizar dimensiones como un solo nivel en el almacenamiento).

La codificación contiene un mapa que proporciona lo siguiente:

Es una secuencia ordenada de especificaciones de dimensiones, cada una de las cuales define lo siguiente:
- el tamaño de la dimensión (implícito a partir de la forma de la dimensión del tensor)
- una expresión-de-dimensión
Una secuencia ordenada de especificaciones de nivel, cada una de las cuales incluye un level-type, que define cómo se debe almacenar el nivel. Cada tipo de nivel se compone de lo siguiente:
- Una level-expression, que define lo que se almacena
- Un formato de nivel
- una colección de level-properties que se aplican al formato de nivel

Cada expresión de nivel es una expresión afín sobre las variables de dimensión. Por lo tanto, el definen de forma colectiva un valor de imagen afín de coordenadas de dimensiones a y coordenadas de nivel. Las expresiones de dimensión definen colectivamente el mapa inverso, que solo debe proporcionarse para casos complicados en los que no se pueda inferir automáticamente.

Cada dimensión también puede tener un SparseTensorDimSliceAttr opcional. En el formato de almacenamiento disperso, nos referimos a los índices que se almacenan explícitamente como coordenadas y desplazamientos en el formato de almacenamiento como posiciones.

Los formatos de niveles compatibles son los siguientes:

dense : todas las entradas de este nivel se almacenan.
composer : solo se almacenan valores distintos de cero en este nivel.
loose_compressed : como comprimido, pero permite un espacio libre entre las regiones
singleton : una variante del formato comprimido, en la que las coordenadas no tienen hermanos
block2_4 : La compresión utiliza una codificación 2:4 por bloque 1x4.

Para un nivel comprimido, cada intervalo de posición se representa en un formato con un límite inferior pos(i) y un límite superior pos(i+1) - 1, lo que implica que deben aparecer en orden sin ningún “agujero” entre los caracteres de ellos. El formato comprimido flexible relaja estas restricciones al representar cada de posición con un lo(i) de límite inferior y un límite superior hi(i), que permite que los intervalos aparezcan en un orden arbitrario y con espacio para los codos entre ellos.

De forma predeterminada, cada tipo de nivel tiene la propiedad de ser único (sin duplicados coordenadas en ese nivel) y en orden (las coordenadas aparecen ordenadas en ese de nivel superior). Se pueden agregar las siguientes propiedades a un formato de nivel para cambiar este comportamiento predeterminado:

no único : coordenadas duplicadas pueden aparecer a nivel
nonordered : las coordenadas pueden aparecer en orden de arbribro.

Además del mapa, los siguientes dos campos son opcionales:

El ancho de bits necesario para el almacenamiento de posiciones (desplazamientos integrales en el esquema de almacenamiento disperso). Un ancho estrecho reduce la memoria de almacenamiento superior, siempre que el ancho sea suficiente para definir el rango total requerido (p. ej., el número máximo de de todos los niveles de indirección). Las opciones son 8, 16, 32, 64 o, el valor predeterminado, 0 para indicar el ancho de bits nativo.
El ancho de bits necesario para el almacenamiento de coordenadas (las coordenadas de entradas almacenadas). Un ancho estrecho reduce el espacio en memoria de sobrecarga de almacenamiento, siempre que el ancho sea suficiente para definir el rango total requerido (vid. el valor máximo de cada tensor coordinar en todos los niveles). Las opciones son 8, 16, 32, 64 o, el valor predeterminado, 0 para indicar un ancho de bits nativo.

Ejemplos

En formato CSR(Compressed Sparse Row) como se muestra a continuación, la codificación de tensor dispersa sería:

#CSR = #sparse_tensor.encoding<{
  map = (i, j) -> (i : dense, j : compressed)
}>

Indica que first dimension (fila) se asigna a first level, que es un nivel dense, indicado por el tamaño 4. Y el second dimension (columna) se asigna al second level, indicado por el array de posiciones y coordenadas. El valor 3 ([1, 1] en la matriz original) es representado por el desplazamiento de la matriz de posiciones (el número de fila del valor 3 es 1 en la matriz original, ya que es el segundo par de desplazamiento y su el número de columna reside en el índice [2 : 4) en el array de coordenadas). Y en la coordenadas, podemos ver que el número de columna del valor 3 es 1 en la de la matriz original.

Para el formato BSR(Block Sparse Row), el tipo de tensor disperso es el siguiente:

#BSR = #sparse_tensor.encoding<{
  map = (i, j) ->
    ( i floordiv 2 : dense
    , j floordiv 2 : compressed
    , i mod 2 : dense
    , j mod 2 : dense
    )

Considera la siguiente matriz dispersa con bloques de 2x2:

Example 2x2 block storage:
 +-----+-----+-----+    +-----+-----+-----+
 | 1 2 | . . | 4 . |    | 1 2 |     | 4 0 |
 | . 3 | . . | . 5 |    | 0 3 |     | 0 5 |
 +-----+-----+-----+ => +-----+-----+-----+
 | . . | 6 7 | . . |    |     | 6 7 |     |
 | . . | 8 . | . . |    |     | 8 0 |     |
 +-----+-----+-----+    +-----+-----+-----+

que finalmente se almacena en un formato con sabor a TACO como

Stored as:
   positions[1]   : 0 2 3
   coordinates[1] : 0 2 1
   values         : 1.000000 2.000000 0.000000 3.000000
                    4.000000 0.000000 0.000000 5.000000
                    6.000000 7.000000 8.000000 0.000000

Que, por cierto, es literalmente la Formato de bloques de NVidia presentado en la documentación de cuSparse.

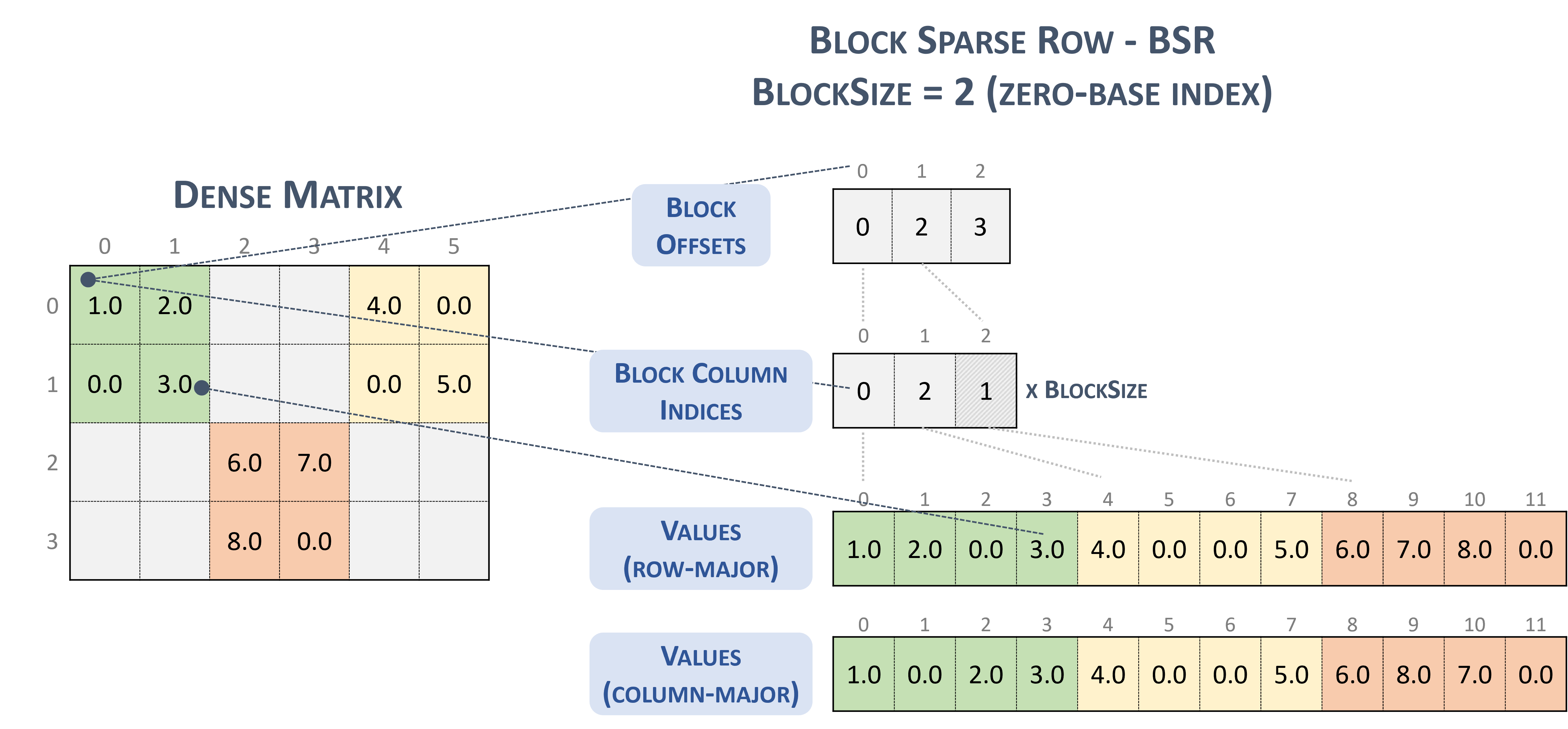
Bloquea fila dispersa. (sin fecha-b). NVIDIA https://docs.nvidia.com/cuda/cusparse/_images/bsr.png

También se admite Nvidia's 2:4 structured sparsity.

El tipo de tensor disperso para esto es el siguiente:

#NV_24 = #sparse_tensor.encoding<{
  map = ( i, j ) -> ( i            : dense,
                      j floordiv 4 : dense,
                      j mod 4      : block2_4),
  crdWidth = 2  // 2-bits for each coordinate
}>

Según la matriz de muestra que se proporciona en la documentación de NVidia:

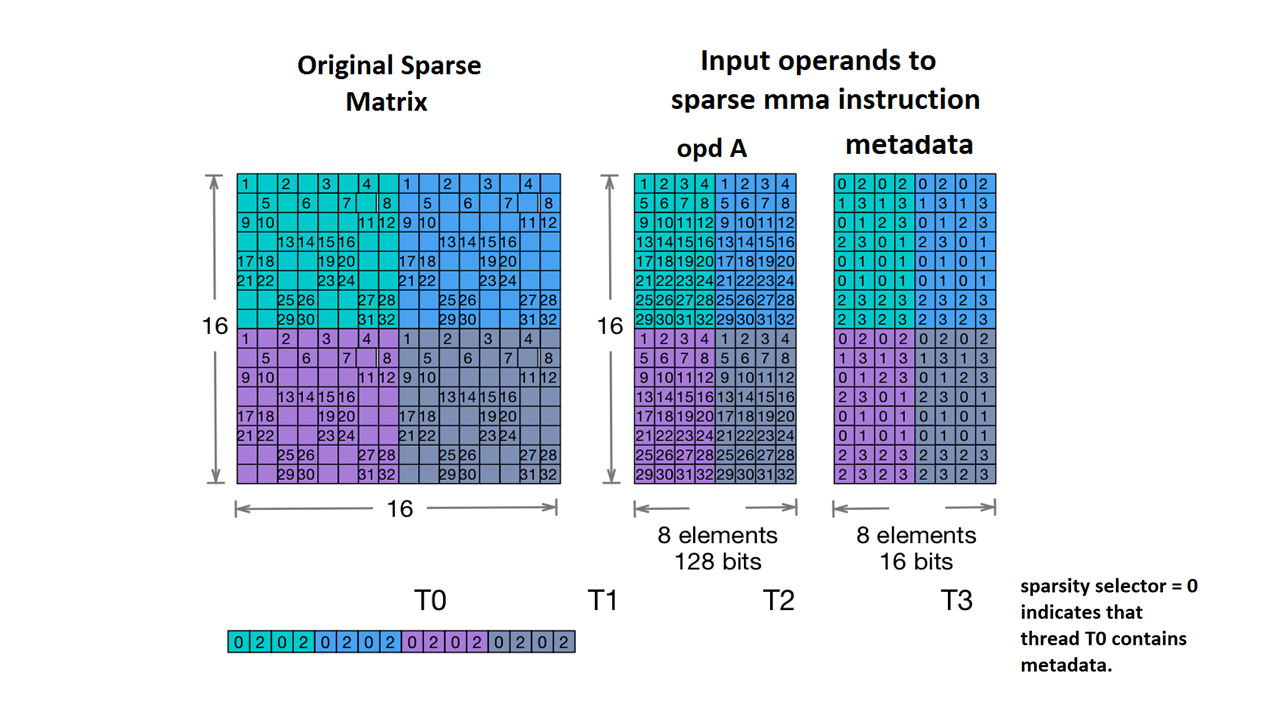
Ejemplo de almacenamiento de MMA disperso. (Sin fecha). NVIDIA https://docs.nvidia.com/cuda/parallel-thread-execution/index.html#warp-level-matrix-instructions-for-sparse-mma

MLIR ahora asigna esta matriz a un diseño idéntico:

coordinates[2]  :
   0 2 0 2 0 2 0 2
   1 3 1 3 1 3 1 3
   0 1 2 3 0 1 2 3
   2 3 0 1 2 3 0 1
   0 1 0 1 0 1 0 1
   0 1 0 1 0 1 0 1
   2 3 2 3 2 3 2 3
   2 3 2 3 2 3 2 3
   0 2 0 2 0 2 0 2
   1 3 1 3 1 3 1 3
   0 1 2 3 0 1 2 3
   2 3 0 1 2 3 0 1
   0 1 0 1 0 1 0 1
   0 1 0 1 0 1 0 1
   2 3 2 3 2 3 2 3
   2 3 2 3 2 3 2 3
values :
  1.000000 2.000000 3.000000 4.000000 1.000000 2.000000 3.000000 4.000000
  5.000000 6.000000 7.000000 8.000000 5.000000 6.000000 7.000000 8.000000
  9.000000 10.000000 11.000000 12.000000 9.000000 10.000000 11.000000 12.000000
  13.000000 14.000000 15.000000 16.000000 13.000000 14.000000 15.000000 16.000000
  17.000000 18.000000 19.000000 20.000000 17.000000 18.000000 19.000000 20.000000
  21.000000 22.000000 23.000000 24.000000 21.000000 22.000000 23.000000 24.000000
  25.000000 26.000000 27.000000 28.000000 25.000000 26.000000 27.000000 28.000000
  29.000000 30.000000 31.000000 32.000000 29.000000 30.000000 31.000000 32.000000
  1.000000 2.000000 3.000000 4.000000 1.000000 2.000000 3.000000 4.000000
  5.000000 6.000000 7.000000 8.000000 5.000000 6.000000 7.000000 8.000000
  9.000000 10.000000 11.000000 12.000000 9.000000 10.000000 11.000000 12.000000
  13.000000 14.000000 15.000000 16.000000 13.000000 14.000000 15.000000 16.000000
  17.000000 18.000000 19.000000 20.000000 17.000000 18.000000 19.000000 20.000000
  21.000000 22.000000 23.000000 24.000000 21.000000 22.000000 23.000000 24.000000
  25.000000 26.000000 27.000000 28.000000 25.000000 26.000000 27.000000 28.000000
  29.000000 30.000000 31.000000 32.000000 29.000000 30.000000 31.000000 32.000000

Más ejemplos:

// Sparse vector.
#SparseVector = #sparse_tensor.encoding<{
  map = (i) -> (i : compressed)
}>
... tensor<?xf32, #SparseVector> ...

// Sorted coordinate scheme.
#SortedCOO = #sparse_tensor.encoding<{
  map = (i, j) -> (i : compressed(nonunique), j : singleton)
}>
... tensor<?x?xf64, #SortedCOO> ...

// Batched sorted coordinate scheme, with high encoding.
#BCOO = #sparse_tensor.encoding<{
  map = (i, j, k) -> (i : dense, j : compressed(nonunique, high), k : singleton)
}>
... tensor<10x10xf32, #BCOO> ...

// Compressed sparse row.
#CSR = #sparse_tensor.encoding<{
  map = (i, j) -> (i : dense, j : compressed)
}>
... tensor<100x100xbf16, #CSR> ...

// Doubly compressed sparse column storage with specific bitwidths.
#DCSC = #sparse_tensor.encoding<{
  map = (i, j) -> (j : compressed, i : compressed),
  posWidth = 32,
  crdWidth = 8
}>
... tensor<8x8xf64, #DCSC> ...

// Block sparse row storage (2x3 blocks).
#BSR = #sparse_tensor.encoding<{
  map = ( i, j ) ->
  ( i floordiv 2 : dense,
    j floordiv 3 : compressed,
    i mod 2      : dense,
    j mod 3      : dense
  )
}>
... tensor<20x30xf32, #BSR> ...

// Same block sparse row storage (2x3 blocks) but this time
// also with a redundant reverse mapping, which can be inferred.
#BSR_explicit = #sparse_tensor.encoding<{
  map = { ib, jb, ii, jj }
        ( i = ib * 2 + ii,
          j = jb * 3 + jj) ->
  ( ib = i floordiv 2 : dense,
    jb = j floordiv 3 : compressed,
    ii = i mod 2 : dense,
    jj = j mod 3 : dense)
}>
... tensor<20x30xf32, #BSR_explicit> ...

// ELL format.
// In the simple format for matrix, one array stores values and another
// array stores column indices. The arrays have the same number of rows
// as the original matrix, but only have as many columns as
// the maximum number of nonzeros on a row of the original matrix.
// There are many variants for ELL such as jagged diagonal scheme.
// To implement ELL, map provides a notion of "counting a
// dimension", where every stored element with the same coordinate
// is mapped to a new slice. For instance, ELL storage of a 2-d
// tensor can be defined with the mapping (i, j) -> (#i, i, j)
// using the notation of [Chou20]. Lacking the # symbol in MLIR's
// affine mapping, we use a free symbol c to define such counting,
// together with a constant that denotes the number of resulting
// slices. For example, the mapping [c](i, j) -> (c * 3 * i, i, j)
// with the level-types ["dense", "dense", "compressed"] denotes ELL
// storage with three jagged diagonals that count the dimension i.
#ELL = #sparse_tensor.encoding<{
  map = [c](i, j) -> (c * 3 * i : dense, i : dense, j : compressed)
}>
... tensor<?x?xf64, #ELL> ...

// CSR slice (offset = 0, size = 4, stride = 1 on the first dimension;
// offset = 0, size = 8, and a dynamic stride on the second dimension).
#CSR_SLICE = #sparse_tensor.encoding<{
  map = (i : #sparse_tensor<slice(0, 4, 1)>,
          j : #sparse_tensor<slice(0, 8, ?)>) ->
        (i : dense, j : compressed)
}>
... tensor<?x?xf64, #CSR_SLICE> ...

Tipos de tensores dispersos en MLIR Organiza tus páginas con colecciones Guarda y categoriza el contenido según tus preferencias.

Ejemplos

Tipos de tensores dispersos en MLIR