Diese Seite wurde von der Cloud Translation API übersetzt.

Dünnbesetzte Tensortypen in MLIR

Die dünnbesetzte Tensor-Codierung ist ein Attribut zum Codieren von Informationen zu dünnen Eigenschaften von Tensoren, durch die TACO-Formalisierung von dünnbesetzten Tensoren. Diese Codierung wird schließlich sparsifier-Pass, um dünnbesetzten Code vollständig automatisch aus einem spärliche Darstellung der Berechnung, d.h. eine implizite dünnbesetzte Darstellung -Darstellung in eine explizite dünnbesetzte Darstellung konvertiert, wobei Co-Itering-Schleifen arbeiten mit geringer Speicherkapazität. Formate anstelle von Tensoren mit einer Dichte Codierung. Compiler-Pässe, die vor diesem Sparsifier-Pass ausgeführt werden, müssen Semantik von Tensortypen mit einer solchen dünnen Codierung.

Bei dieser Codierung verwenden wir dimension: auf die Achsen des semantischen Tensors, und level für die Achsen des tatsächlichen Speicherformats, d.h. die des dünnbesetzten Tensors im Speicher. Die Anzahl der ist normalerweise mit Anzahl der Ebenen (z. B. Speicherformat für CSR) Die Codierung kann jedoch auch Dimensionen auf höhere Ebenen (z. B. zum Codieren eines dünnbesetzten BSR-Speicherformats) oder zu niedrigeren Ebenen (z. B. um Dimensionen als eine Ebene im Speicher zu linearisieren).

Die Codierung enthält eine Karte, die Folgendes bereitstellt:

Eine geordnete Abfolge von Dimensionsspezifikationen, die jeweils Folgendes definieren: <ph type="x-smartling-placeholder">
- die Dimensionsgröße (impliziert von der Dimensionsform des Tensors)
- einen Dimensionsausdruck
Eine geordnete Abfolge von Levelspezifikationen, die jeweils eine erforderliche level-type definiert, wie die Ebene gespeichert werden soll. Jeder Leveltyp besteht aus: <ph type="x-smartling-placeholder">
- einen level-expression, der definiert, was gespeichert wird
- ein Level-Format
- eine Sammlung von level-properties, die für das Level-Format gelten

Jeder Ebenenausdruck ist ein affiner Ausdruck im Vergleich zu Dimensionen-Variablen. Das heißt, die Level-Ausdrücke definieren kollektiv einen affine Map von Dimensionskoordinaten zu Ebenenkoordinaten. Die Dimensionsausdrücke die Inverse Map kollektiv, die nur für komplexe Fälle angegeben werden muss, in denen sie nicht abgeleitet werden kann. automatisch.

Jede Dimension kann auch eine optionale SparseTensorDimSliceAttr haben. Im Sparse-Speicher-Format beziehen wir uns auf Indexe, die explizit als Koordinaten und Offsets in das Speicherformat positions ein.

Folgende Ebenenformate werden unterstützt:

dense : Alle Einträge auf dieser Ebene werden gespeichert.
komprimiert : Nur Nullwerte auf dieser Ebene werden gespeichert.
loose_compressed : wie komprimiert, aber es lässt freien Speicherplatz zwischen Regionen zu.
singleton : eine Variante des komprimierten Formats, bei der die Koordinaten keine gleichgeordneten Elemente haben
block2_4 : Die Komprimierung verwendet eine 2:4-Codierung pro 1x4-Block.

Bei komprimierter Ebene wird jedes Positionsintervall in einem kompakten mit einer Untergrenze pos(i) und einer Obergrenze pos(i+1) - 1, die impliziert, dass aufeinanderfolgende Intervalle der Reihe nach ohne „Löcher“ angezeigt werden müssen. dazwischen . Das lose komprimierte Format lockert diese Einschränkungen, indem Positionsintervall mit einer Untergrenze lo(i) und einer Obergrenze hi(i), die können Intervalle in beliebiger Reihenfolge und mit ausreichendem Platz dazwischen erscheinen.

Standardmäßig hat jeder Ebenentyp die Eigenschaft, eindeutig (keine doppelten auf dieser Ebene) und sortiert (die Koordinaten werden dort Level). Die folgenden Eigenschaften können einem Ebenenformat hinzugefügt werden, um dieses Standardverhaltens:

nonunique : in der Ebene dürfen Koordinaten doppelt vorhanden sein.
nonordered : Koordinaten können in der Arbribratry-Reihenfolge angezeigt werden.

Zusätzlich zur Karte sind die folgenden zwei Felder optional:

Erforderliche Bitbreite für Positionsspeicher (integrale Offsets) in das dünnbesetzte Speicherschema integriert. Eine schmale Breite reduziert den Arbeitsspeicher Platzbedarf, solange die Breite ausreicht, den gesamten erforderlichen Bereich (d. h. die maximale Anzahl der Einträgen für alle Indirektionsebenen). Zur Auswahl stehen 8, 16, 32, 64 oder der Standardwert 0, um die native Bitbreite anzugeben.
Die erforderliche Bitbreite für die Koordinatenspeicherung (die Koordinaten gespeicherter Einträge). Eine geringe Breite reduziert den Speicherbedarf. des Overhead-Speichers verwendet, solange die Breite ausreicht, den insgesamt erforderlichen Bereich (d. h. den Maximalwert jedes Tensors) Koordinaten auf allen Ebenen). Zur Auswahl stehen 8, 16, 32, 64 oder der Standardwert 0, um eine native Bitbreite anzugeben.

Beispiele

Im Format CSR(Compressed Sparse Row) die dünnbesetzte Tensor-Codierung wäre:

#CSR = #sparse_tensor.encoding<{
  map = (i, j) -> (i : dense, j : compressed)
}>

Es gibt an, dass die first dimension (Zeile) dem first level, Dies ist ein dense-Level, der durch Größe 4 angegeben wird. Und die second dimension (Spalte) ist dem second level zugeordnet, angegeben durch das Array „positions“ und -Koordinaten-Array. Der Wert 3 ([1, 1] in der ursprünglichen Matrix) ist dargestellt durch den Versatz von Positionens-Array (Zeilennummer von 3) ist 1 in der ursprünglichen Matrix, da es das zweite Offset-Paar ist und seine Spaltennummer befindet sich im Index [2 : 4) des Koordinatenarrays. In der -Koordinaten-Array schreiben, sehen wir, dass die Spaltennummer des Werts 3 1 im die ursprüngliche Matrix.

Für das Format BSR(Block Sparse Row) ist der dünnbesetzte Tensortyp:

#BSR = #sparse_tensor.encoding<{
  map = (i, j) ->
    ( i floordiv 2 : dense
    , j floordiv 2 : compressed
    , i mod 2 : dense
    , j mod 2 : dense
    )

Betrachten Sie die folgende dünnbesetzte Matrix mit 2x2-Blöcken:

Example 2x2 block storage:
 +-----+-----+-----+    +-----+-----+-----+
 | 1 2 | . . | 4 . |    | 1 2 |     | 4 0 |
 | . 3 | . . | . 5 |    | 0 3 |     | 0 5 |
 +-----+-----+-----+ => +-----+-----+-----+
 | . . | 6 7 | . . |    |     | 6 7 |     |
 | . . | 8 . | . . |    |     | 8 0 |     |
 +-----+-----+-----+    +-----+-----+-----+

das schließlich im TACO-Format gespeichert wird,

Stored as:
   positions[1]   : 0 2 3
   coordinates[1] : 0 2 1
   values         : 1.000000 2.000000 0.000000 3.000000
                    4.000000 0.000000 0.000000 5.000000
                    6.000000 7.000000 8.000000 0.000000

Das ist übrigens NVidia-Blockformat in der cuSparse-Dokumentation.

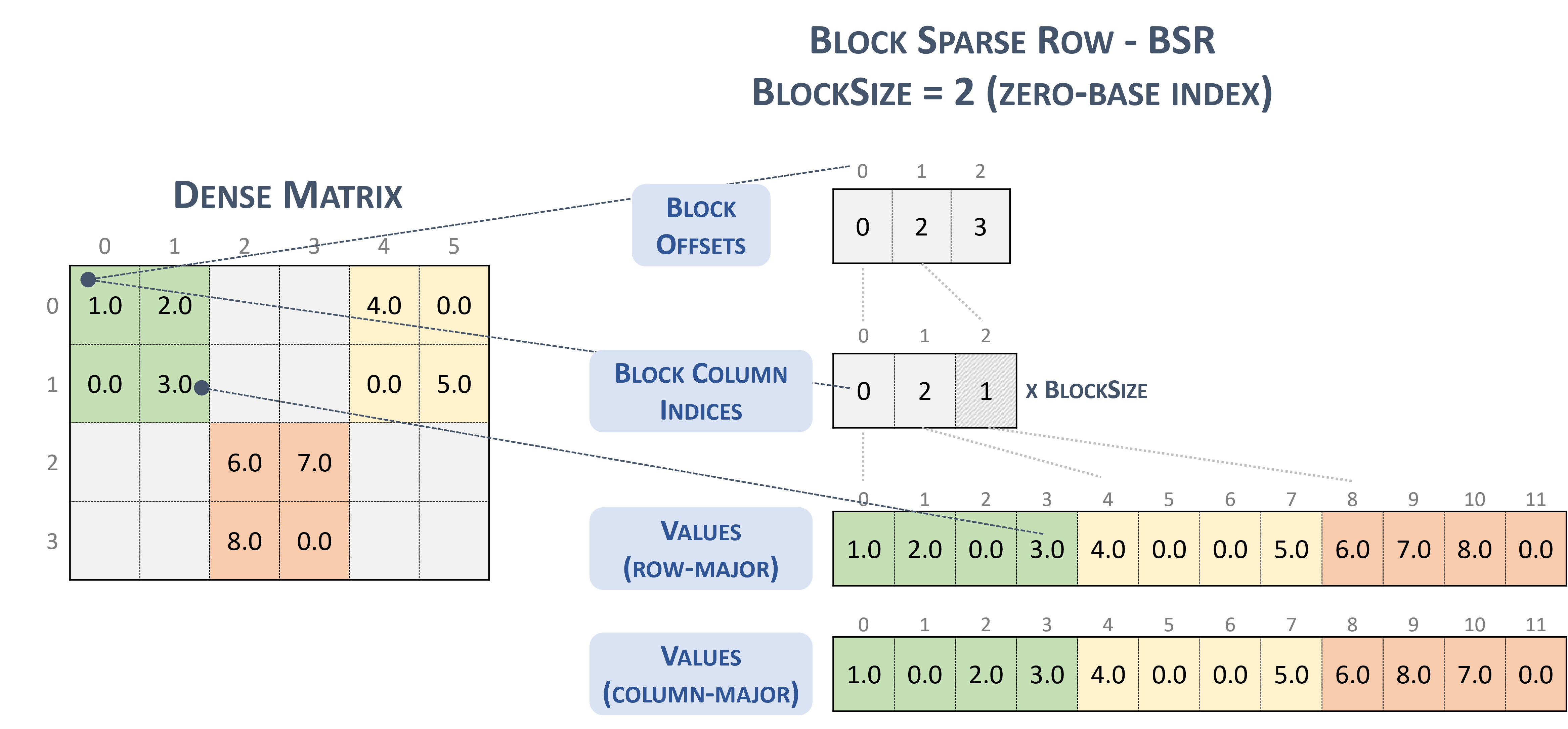
Sparse-Zeile blockieren: (ohne Datum; b): NVIDIA https://docs.nvidia.com/cuda/cusparse/_images/bsr.png

Wir unterstützen auch Nvidia's 2:4 structured sparsity.

Der dünnbesetzte Tensortyp dafür ist so:

#NV_24 = #sparse_tensor.encoding<{
  map = ( i, j ) -> ( i            : dense,
                      j floordiv 4 : dense,
                      j mod 4      : block2_4),
  crdWidth = 2  // 2-bits for each coordinate
}>

Anhand der Beispielmatrix aus der NVidia-Dokumentation:

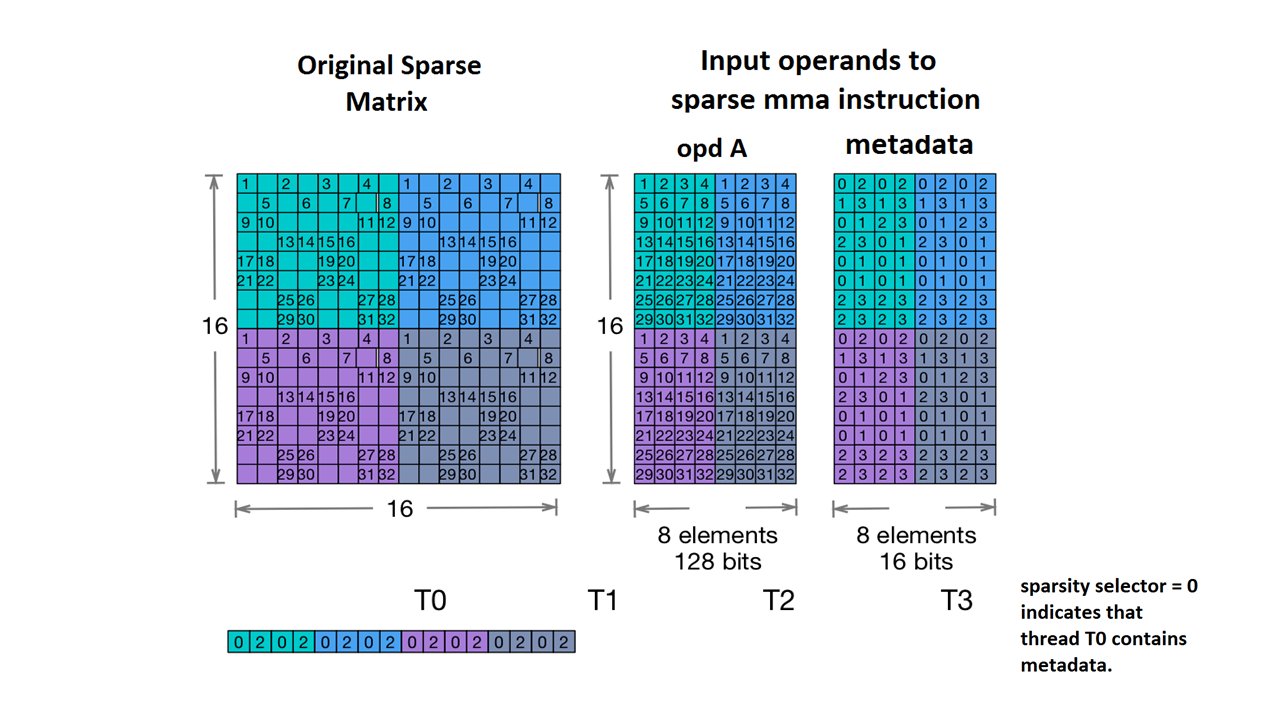
Beispiel für eine dünnbesetzte MMA-Speicherung (ohne Datum). NVIDIA https://docs.nvidia.com/cuda/parallel-thread-execution/index.html#warp-level-matrix-instructions-for-sparse-mma

MLIR ordnet diese Matrix jetzt einem identischen Layout zu:

coordinates[2]  :
   0 2 0 2 0 2 0 2
   1 3 1 3 1 3 1 3
   0 1 2 3 0 1 2 3
   2 3 0 1 2 3 0 1
   0 1 0 1 0 1 0 1
   0 1 0 1 0 1 0 1
   2 3 2 3 2 3 2 3
   2 3 2 3 2 3 2 3
   0 2 0 2 0 2 0 2
   1 3 1 3 1 3 1 3
   0 1 2 3 0 1 2 3
   2 3 0 1 2 3 0 1
   0 1 0 1 0 1 0 1
   0 1 0 1 0 1 0 1
   2 3 2 3 2 3 2 3
   2 3 2 3 2 3 2 3
values :
  1.000000 2.000000 3.000000 4.000000 1.000000 2.000000 3.000000 4.000000
  5.000000 6.000000 7.000000 8.000000 5.000000 6.000000 7.000000 8.000000
  9.000000 10.000000 11.000000 12.000000 9.000000 10.000000 11.000000 12.000000
  13.000000 14.000000 15.000000 16.000000 13.000000 14.000000 15.000000 16.000000
  17.000000 18.000000 19.000000 20.000000 17.000000 18.000000 19.000000 20.000000
  21.000000 22.000000 23.000000 24.000000 21.000000 22.000000 23.000000 24.000000
  25.000000 26.000000 27.000000 28.000000 25.000000 26.000000 27.000000 28.000000
  29.000000 30.000000 31.000000 32.000000 29.000000 30.000000 31.000000 32.000000
  1.000000 2.000000 3.000000 4.000000 1.000000 2.000000 3.000000 4.000000
  5.000000 6.000000 7.000000 8.000000 5.000000 6.000000 7.000000 8.000000
  9.000000 10.000000 11.000000 12.000000 9.000000 10.000000 11.000000 12.000000
  13.000000 14.000000 15.000000 16.000000 13.000000 14.000000 15.000000 16.000000
  17.000000 18.000000 19.000000 20.000000 17.000000 18.000000 19.000000 20.000000
  21.000000 22.000000 23.000000 24.000000 21.000000 22.000000 23.000000 24.000000
  25.000000 26.000000 27.000000 28.000000 25.000000 26.000000 27.000000 28.000000
  29.000000 30.000000 31.000000 32.000000 29.000000 30.000000 31.000000 32.000000

Weitere Beispiele:

// Sparse vector.
#SparseVector = #sparse_tensor.encoding<{
  map = (i) -> (i : compressed)
}>
... tensor<?xf32, #SparseVector> ...

// Sorted coordinate scheme.
#SortedCOO = #sparse_tensor.encoding<{
  map = (i, j) -> (i : compressed(nonunique), j : singleton)
}>
... tensor<?x?xf64, #SortedCOO> ...

// Batched sorted coordinate scheme, with high encoding.
#BCOO = #sparse_tensor.encoding<{
  map = (i, j, k) -> (i : dense, j : compressed(nonunique, high), k : singleton)
}>
... tensor<10x10xf32, #BCOO> ...

// Compressed sparse row.
#CSR = #sparse_tensor.encoding<{
  map = (i, j) -> (i : dense, j : compressed)
}>
... tensor<100x100xbf16, #CSR> ...

// Doubly compressed sparse column storage with specific bitwidths.
#DCSC = #sparse_tensor.encoding<{
  map = (i, j) -> (j : compressed, i : compressed),
  posWidth = 32,
  crdWidth = 8
}>
... tensor<8x8xf64, #DCSC> ...

// Block sparse row storage (2x3 blocks).
#BSR = #sparse_tensor.encoding<{
  map = ( i, j ) ->
  ( i floordiv 2 : dense,
    j floordiv 3 : compressed,
    i mod 2      : dense,
    j mod 3      : dense
  )
}>
... tensor<20x30xf32, #BSR> ...

// Same block sparse row storage (2x3 blocks) but this time
// also with a redundant reverse mapping, which can be inferred.
#BSR_explicit = #sparse_tensor.encoding<{
  map = { ib, jb, ii, jj }
        ( i = ib * 2 + ii,
          j = jb * 3 + jj) ->
  ( ib = i floordiv 2 : dense,
    jb = j floordiv 3 : compressed,
    ii = i mod 2 : dense,
    jj = j mod 3 : dense)
}>
... tensor<20x30xf32, #BSR_explicit> ...

// ELL format.
// In the simple format for matrix, one array stores values and another
// array stores column indices. The arrays have the same number of rows
// as the original matrix, but only have as many columns as
// the maximum number of nonzeros on a row of the original matrix.
// There are many variants for ELL such as jagged diagonal scheme.
// To implement ELL, map provides a notion of "counting a
// dimension", where every stored element with the same coordinate
// is mapped to a new slice. For instance, ELL storage of a 2-d
// tensor can be defined with the mapping (i, j) -> (#i, i, j)
// using the notation of [Chou20]. Lacking the # symbol in MLIR's
// affine mapping, we use a free symbol c to define such counting,
// together with a constant that denotes the number of resulting
// slices. For example, the mapping [c](i, j) -> (c * 3 * i, i, j)
// with the level-types ["dense", "dense", "compressed"] denotes ELL
// storage with three jagged diagonals that count the dimension i.
#ELL = #sparse_tensor.encoding<{
  map = [c](i, j) -> (c * 3 * i : dense, i : dense, j : compressed)
}>
... tensor<?x?xf64, #ELL> ...

// CSR slice (offset = 0, size = 4, stride = 1 on the first dimension;
// offset = 0, size = 8, and a dynamic stride on the second dimension).
#CSR_SLICE = #sparse_tensor.encoding<{
  map = (i : #sparse_tensor<slice(0, 4, 1)>,
          j : #sparse_tensor<slice(0, 8, ?)>) ->
        (i : dense, j : compressed)
}>
... tensor<?x?xf64, #CSR_SLICE> ...

Dünnbesetzte Tensortypen in MLIR Mit Sammlungen den Überblick behalten Sie können Inhalte basierend auf Ihren Einstellungen speichern und kategorisieren.

Beispiele

Dünnbesetzte Tensortypen in MLIR