Wiele problemów wymaga podania wartości szacunkowej jako danych wyjściowych. Regresja logistyczna to bardzo skuteczny mechanizm obliczania prawdopodobieństwa. W praktyce oznacza to, że zwrot wartości można zastosować na 2 sposoby:
- "
- Przekonwertowano na kategorię binarną.
Weźmy pod uwagę to, jak wykorzystamy prawdopodobieństwo w takiej postaci, w jakiej jest. Załóżmy, że opracowujemy model regresji logicznej, który pozwala przewidzieć prawdopodobieństwo tego, że pies będzie szczekać w środku nocy. Prawdopodobieństwo to:
\[p(bark | night)\]
Jeśli prognoza regresji logicznej przewiduje \(p(bark | night) = 0.05\), to w ciągu roku właściciel psa powinien zacząć się budzić ok. 18 razy:
\[\begin{align} startled &= p(bark | night) \cdot nights \\ &= 0.05 \cdot 365 \\ &~= 18 \end{align} \]
W wielu przypadkach zmapujesz dane regresyjne logistyki na rozwiązanie do problemu z klasyfikacją binarną, w której celem jest prawidłowa przewidywalność jednej z dwóch etykiet (np. "spam" &&tt;not spam"). Następnie skupi się na tym moduł.
Być może zastanawiasz się, jak model regresji logistycznej może sprawić, że dane wyjściowe będą zawsze mieścić się w zakresie od 0 do 1. W takiej sytuacji funkcja sigmoidowa zdefiniowana w ten sposób daje wyniki o tych samych cechach:
Funkcja sigmoid generuje taki wykres:
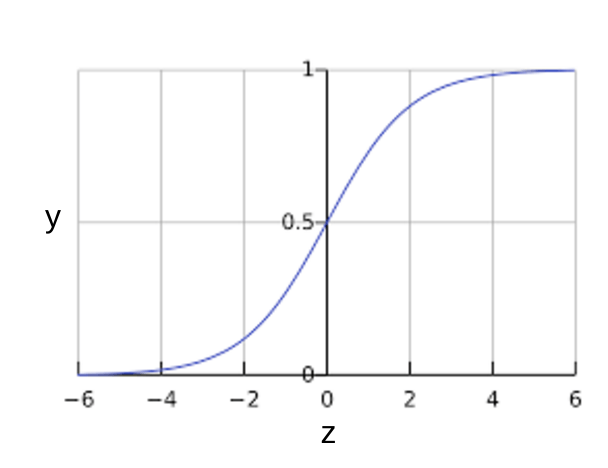
Rysunek 1. Funkcja sigmoidowa
Jeśli \(z\) odzwierciedla dane wyjściowe warstwy liniowej modelu wytrenowanego za pomocą regresji logicznej, \(sigmoid(z)\) uzyska wartość (prawdopodobieństwo) od 0 do 1. W kontekście matematycznym:
gdzie:
- \(y'\) to dane wyjściowe modelu regresji logicznej dla danego przykładu.
- \(z = b + w_1x_1 + w_2x_2 + \ldots + w_Nx_N\)
- Wartości \(w\) to model nauczony wagi, \(b\) to odchylenia.
- Wartości \(x\) to wartości cech określonego przykładu.
Zwróć uwagę, że \(z\) jest też nazywany logiem nieparzystym, ponieważ odwrotność sigmoidów, które można zdefiniować \(z\) jako log prawdopodobieństwa \(1\) etykiety (np. &&tt; szczeki dla psów") podzielone przez prawdopodobieństwo \(0\)etykiety (np. "pies nie
Oto funkcja sigmoid z etykietami ML:
Rysunek 2. Dane regresyjne logistyki wyjściowej
Kliknij ikonę plusa, aby zobaczyć przykładowe obliczanie regresji logistyki.
Załóżmy, że mamy model regresji logistycznej, w którym występują trzy cechy, które wykrywają następujące odchylenia i wagi:
$$\begin{align} b &= 1 \\ w_1 &= 2 \\ w_2 &= -1 \\ w_3 &= 5 \end{align} $$Przyjmijmy też, że dla danego przykładu podane są następujące wartości cech:
$$\begin{align} x_1 &= 0 \\ x_2 &= 10 \\ x_3 &= 2 \end{align} $$W związku z tym:
będzie:
$$(1) + (2)(0) + (-1)(10) + (5)(2) = 1$$W związku z tym prognoza regresji logistycznej w tym przykładzie będzie wynosić 0, 731:
Rysunek 3: 73,1% prawdopodobieństwa.