在图 1 和图 2 中,我们做出如下假设:
- 蓝点代表生病的树。
- 橙色的点代表健康的树。
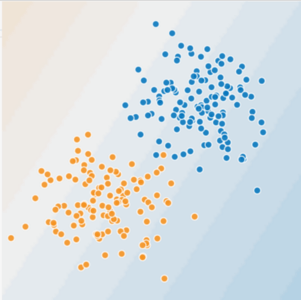
图 1. 这是一个线性问题吗?
您可以画一条线将生病的树与健康的树清晰地分开吗?没问题,这是一个线性问题。这条线并不完美。一只生病的树可能在“健康”一端,但您的线条会很好地预测。
现在,请参考下图:
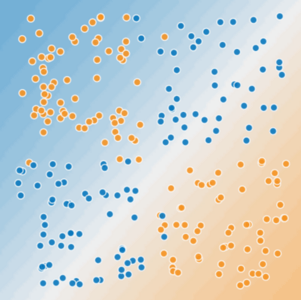
图 2. 这是一个线性问题吗?
您可以绘制一条直线将生病的树与健康的树清晰地分开吗?不可以。这是一个非线性问题。您绘制的任何线条都无法很好地预测树的健康状况。
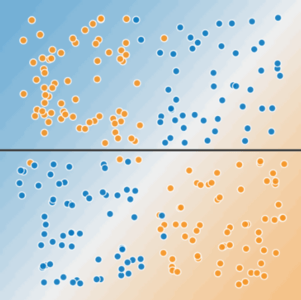
图 3. 一行代码无法分隔这两个类。
如需解决图 2 中所示的非线性问题,请创建一个特征组合。特征组合是指通过将两个或多个输入特征相乘来对特征空间中的非线性特征进行编码的合成特征。(术语跨来自跨产品。) 下面我们通过组合 \(x_3\) 和 \(x_2\)来创建一个名为“ \(x_3\) ”的特征组合:
$$x_3 = x_1x_2$$
我们将这个新生成的 \(x_3\) 特征组合与任何其他特征视为一样。线性公式变为:
$$y = b + w_1x_1 + w_2x_2 + w_3x_3$$
线性算法可以像计算 \(w_1\) 和 \(w_2\)一样学习 \(w_3\)的权重。换言之,虽然 \(w_3\) 会对非线性信息进行编码,但您无需更改线性模型的训练方式即可确定 \(w_3\)的值。
特征组合的种类
我们可以创建许多不同类型的特征组合。例如:
[A X B]:将两个特征的值相乘形成的特征组合。[A x B x C x D x E]:将五个特征的值相乘形成的特征组合。[A x A]:通过对单个特征求平方形成的特征组合。
通过采用随机梯度下降法,可以有效地训练线性模型。因此,使用特征组合补充缩放的线性模型一直是对大规模数据集进行训练的高效方法。
